文献あり

代数としての木と順序関係

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

箱星さんによる木 Advent Calendar 2025 の6日目の記事です。(遅刻なので実質7日目ですが...。)
木についてならなんでもよいということらしいので、今回は代数を木上の同値関係という面で見てみます。また、似たような方法で木上の順序関係についても色々語っていきます。

代数

代数とは、集合と、その集合上のいくつかの演算の組のことを指します。
具体例をいくつか見てみましょう。

自然数全体の集合$\mathbb N$と加法$+$の組$(\mathbb N,+)$
自然数全体の集合$\mathbb N$と加法$+$と関数$f ; (x,y,z) \mapsto x^{y^x+z} + 10000y$の組$(\mathbb N,+,f)$
集合$X$の冪集合$P(X)$と空集合$\emptyset$と全体集合$X$と交叉$\cap$と和集合$\cup$と補集合${}^c$の組$(P(X),\emptyset,X,\cap,\cup,^c)$
複素数全体の集合$\mathbb C$と加法$+$と各実数$r$に対する関数$f_r ; (a+bi) \mapsto (ar + bri)$の組$(\mathbb C,+,\{f_r\}_{r \in \mathbb R})$

例に挙げた通り、組とする演算は複数(特に無限個)あっても構いません。
また、特定の綺麗な性質を満たす必要はなく、$f ; (x,y,z) \mapsto x^{y^x+z} + 10000y$みたいな変なものも演算としてよいです。
集合$S$上の演算は、ある非負整数$n$について、$S^n$から$S$への写像の形であればなんでもよいです。特に、$S^0 \to S$の形の写像は実質的に$S$の1つの元を表しているので、$0$変数演算として$S$の元を組として入れても問題ないです。

我々がよく「代数」と呼ぶものは、組となる演算の個数やそれら演算が何項演算なのかを揃えて、更に諸公理を満たしたもののみを考えることがほとんどです。
例えば、
組となる演算として二項演算$*$を1つだけ持つ代数をマグマと呼んだり、
マグマのうち二項演算が結合法則を満たすものを半群と呼んだり、
半群のうち単位元をもつもの(あるいは$e$を$0$項演算として加えたもののうち、各元$a$について$a * e = e * a = a$を満たすもの)をモノイドと呼んだり、
更に逆元の存在(あるいは逆元操作に相当する$1$項演算を導入し、その演算が逆元の性質を満たすもの)をモノイドを群と呼んだりします。

代数と木

さて、演算を用いて表現された元は、「構文木」という頂点がラベルづけられた根付き木とみなせます。
例えば、3項演算$f$、1項演算$g,h$をもつ代数にて、元$x,y,z$と演算を用いて表された元には$f(x,g(z),f(g(h(x)),y,z))$のような元がありますが、これは以下の図のような根付き木として表現できます。

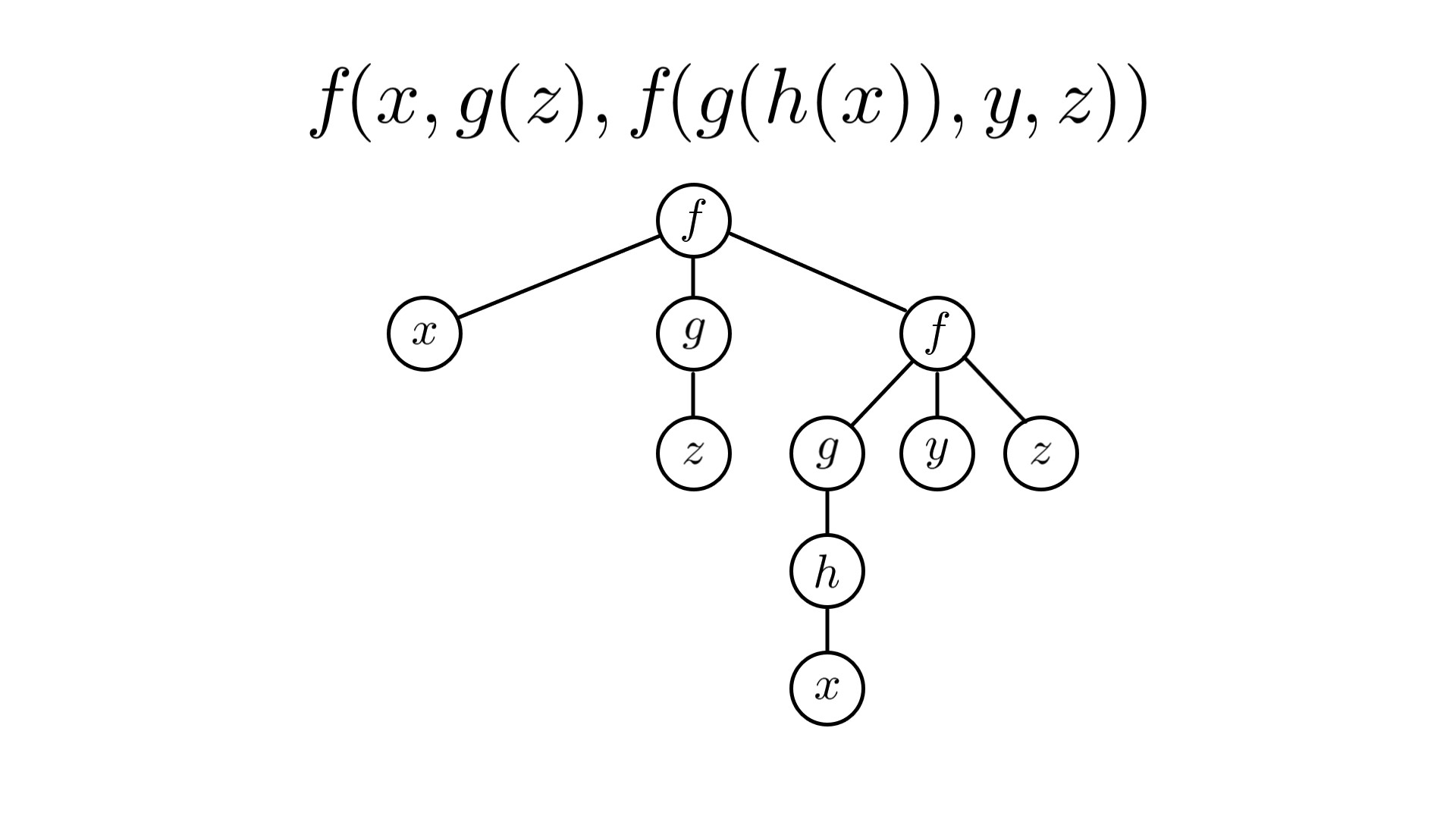構文木

$X$を集合とした代数で、元$x \in X$が部分集合$S \subseteq X$の元と代数の演算のみによって表される($S$の元と演算のみによる構文木で表される)とき、「$x$は$S$によって生成される」といいます。
例えば代数$(\mathbb N,+)$にて、部分集合$\{4,6\}$によって生成される元は、$4,6,8,10,12,\cdots$のように$4$以上の偶数となります。

ところで、$S$の生成元は、$S$の元と演算によって表す方法は一意とは限りません。すなわち、$S$によって生成される元$x$は、その構文木が2つ以上あることもあります。
例えば代数$(\mathbb N,+)$にて、$10$は部分集合$\{4,6\}$によって生成される元ですが、$4+6$とも$6+4$とも表せます。
見方を変えれば、これは2つの異なる構文木を同一視して"$10$"という数として扱っている、というようにも見なせます。

ここで一度、構文木そのものを元として代数を構成してみましょう。

項代数

集合$A$、及び各自然数$n$に対して集合$F_n$がそれぞれ互いに交わらないとき、$A \cup \bigcup_{n \in \mathbb N}F_n$の元を形式的な記号として、以下のように記号列の集合を定義する。

$T_0 := A$
$T_{i+1} := A \cup \bigcup_{n \in \mathbb N} \{f(t_0,t_1,\cdots,t_{n-1}) \mid f \in F_n \land t_0,t_1,\cdots,t_{n-1} \in T_i\}$
$T := \bigcup_{i \in \mathbb N} T_i$

このようにして得た記号列の集合$T$について、$(T,F_0,F_1,\cdots)$は代数をなす。各自然数$n$について、$f \in F_n$は$T$上の$n$項演算である。

このように構成した代数は、$\bigcup_{n \in \mathbb N} F_n$の元を全て演算としてもつ代数であり、任意の元は$A$によって生成されます。記号列として定義しましたが、本質的には$A \cup \bigcup_{n \in \mathbb N}$の元をラベルにもつ構文木全体の集合です。
特に、$A,F_0$の元でラベルづけられた頂点は葉となり、$F_n$の元でラベルづけられた頂点はちょうど$n$個の子頂点を持ちます。
$F_n$の元$f$と構文木$t_0,t_1,\cdots,t_{n-1}$があったとき、$f$でラベルづけられた頂点を根として、その頂点に$t_0,t_1,\cdots,t_{n-1}$の根からそれぞれ辺を伸ばせば新たな木が作れるので、これによって$f$を$n$項演算とみなすということになります。

この項代数の元を適切に同一視すれば、$(\mathbb N,+)$などの代数も作れそうです。つまり、項代数に同値関係を定めてやります。
しかし、同値関係であればなんでもよいわけではありません。例えば、$A = \{x\},\ F_1 = \{f\},\ F_0 = F_2 = F_3 = F_4 = \cdots = \emptyset$として項代数を作ってみると、$T = \{x,f(x),f(f(x)),f(f(f(x))),\cdots\}$となります。ここで$T$上の同値関係$\sim$を、$x \sim f(x),\ f(x) \sim x,\ $及び各$t \in T$について$t \sim t$のみが成り立つようなものとします。
定義から$x \sim f(x)$ですが、$f(x) \sim f(f(x))$ではありません。これはなんとも気持ち悪いです。同一視されてるものなのに、同じ演算を施したら同一視されなくなるというのは変です。
(いわゆる商における演算のwell-defined性というものが成り立ってません。)
というわけで、そういった変な同値関係を省くために、合同関係というものを定義します。

合同関係

項代数$(T,F_0,F_1,\cdots)$について、合同関係とは$T$上の二項関係$\sim$のうち、以下を満たすものである。

任意の$a \in T$について、$a \sim a$
任意の$a,b \in T$について、$a \sim b$ならば$b \sim a$
任意の$a,b,c \in T$について、$a \sim b$かつ$b \sim c$ならば$a \sim c$
任意の$n \in \mathbb N$と$f \in F_n$と$a_0,\cdots,a_{n-1},b_0,\cdots,b_{n-1} \in T$について、各$0 \le i < n$に対して$a_i \sim b_i$が成り立つならば、$f(a_0,\cdots,a_{n-1}) \sim f(b_0,\cdots,b_{n-1})$

最初の3つの条件は同値関係であるという主張であり、最後の条件は「同一視されてるものに同じ演算を施しても同一視されたままである」という主張です。

あらゆる代数は、項代数の元を合同関係で同一視したもの(商代数)とみなせます。
例えば、$(\mathbb N,+)$はどの元も$\{0,1\}$によって生成されるが、これは$A = \{0,1\},\ F_2 = \{+\},\ F_0 = F_1 = F_3 = \cdots = \emptyset$とした項代数$(T,+)$を、各$s,t,u \in T$について$t + 0 \sim 0 + t \sim t$と$(s+t)+u \sim s+(t+u)$を満たす最も弱い合同関係$\sim$で同一視したものです。
また、$F_0 = \{e\},\ F_1 = \{\textrm{inv}\},\ F_2 = \{*\},\ F_3 = F_4 = \cdots = \emptyset$とした項代数$(T,e,\textrm{inv},*)$を、各$s,t,u \in T$について$t * e \sim e * t \sim t$と$(s*t)*u \sim s*(t*u)$と$t * \textrm{inv}(t) \sim \textrm{inv}(t) * t \sim e$を満たす同値関係$\sim$で同一視すれば群となり、更に$\sim$を最も弱いものにすると$A$によって生成される自由群となります。

このように、構文木に対して演算によって保存される同値関係を入れると、代数を得ることができます。

木の順序

構文木に対して演算によって保存される同値関係を入れると代数ができました。
では、演算によって保存される前順序関係を入れるとどうなるでしょうか？

この場合、$s \le t$かつ$t \le s$を満たす構文木$s,t$を同一視することで同じように代数が得られます。また、得られた代数でも演算によって順序が保存されます。
代数における演算が全て順序保存、というのは一見面白そうですが、例えば順序群は積が順序保存であるものの、逆元を取る演算は順序保存ではない(順序反変ではある)ので、代数の全ての演算が順序保存となるようなものは案外扱いづらいのかもしれません。
(筆者がパッと思いつくような演算が全て順序保存となる代数は、束くらいしかありません。知識不足ですみません...。)

しかし、もう1つ条件を加えると、とても面白い性質が現れます。

項順序

項代数$(T,F_0,F_1,\cdots)$について、項順序とは$T$上の二項関係$\le$のうち、以下を満たすものである。

任意の$a \in T$について、$a \le a$
任意の$a,b,c \in T$について、$a \le b$かつ$b \le c$ならば$a \le c$
任意の$n \in \mathbb N$と$f \in F_n$と$a_0,\cdots,a_{n-1} \in T$について、各$0 \le i < n$に対して$a_i \le f(a_0,\cdots,a_{n-1})$
任意の$n \in \mathbb N$と$f \in F_n$と$a_0,\cdots,a_{n-1},b_0,\cdots,b_{n-1} \in T$について、各$0 \le i < n$に対して$a_i \le b_i$が成り立つならば、$f(a_0,\cdots,a_{n-1}) \le f(b_0,\cdots,b_{n-1})$

最初の2つの条件は、$\le$が前順序となることで、最後の条件は$\le$がどの演算でも保存されることを表します。
3つ目の条件は、演算に使った元よりも演算結果の元の方が大きいということを表しています。

このような順序について、以下のような定理が知られています。

Kruskalの木定理

$\le$を項代数$(T,F_0,F_1,\cdots)$の項順序の1つとする。
$A \cup \bigcup_{n \in \mathbb N}F_i$が有限集合であるとき、$T$の元の列$\{t_i\}_{i \in \mathbb N}$について、$i < j$かつ$t_i \le t_j$を満たす$i,j \in \mathbb N$が存在する。

(もう少し項順序の定義を改良することで、$A,F_0,F_1,\cdots$のうち有限個を除き空集合であり、更に$A,F_0,F_1,\cdots$のいずれも整擬順序である場合にまで仮定を弱めることもできたりしますが、説明がめんどいので省略します。)

一見何が嬉しいのかよくわからない定理かもしれません。
Kruskalの木定理のように、任意の無限列$\{t_i\}_{i \in \mathbb N}$について、$i < j$かつ$t_i \le t_j$を満たす$i,j \in \mathbb N$が存在するような順序$\le$を整擬順序とよびます。
整擬順序には同値条件が様々あり、特にグラフ理論では、「グラフの多くの幾何的性質に対して、次数$3$の多項式時間で判定するアルゴリズムが存在する」ということを示す際に必要になるようです。
また、整擬順序は整列順序と性質が似ており、整擬順序を拡張して全順序にしたものは必ず整列順序になるので、帰納法を扱いやすいという利点もあったりします。

今回のKruskalの木定理は、演算が全て順序保存で$a_i \le f(a_0,\cdots,a_{n-1})$を満たす、有限生成で演算が有限個しかない擬順序付き代数は、その順序が必ず整擬順序となるという極めて強い主張となります。

最後に、Kruskalの木定理の帰結の1つを紹介します。

導火線で測れる時間は整列順序をなす

両側に任意のタイミングで火をつけられる導火線が存在する。この導火線は片方に火をつけて待てばちょうど$1$分で燃え尽き、反対側に火をつけると燃え尽きるまでの残り時間が半減する。
最初の導火線に火をつけた瞬間から数えて、導火線が燃え尽きたと同時に他の導火線に火をつけるという操作だけで測れる時間を可融数とよぶ。
可融数は、$0$または、$|a-b| < 1$を満たす可融数$a,b$を用いて$\dfrac{a+b+1}2$と表されることが知られている。

可融数全体の集合を$M$とし、$M$上の二項演算$f$を、$|a-b| < 1$ならば$f(a,b) := \dfrac{a+b+1}2$、そうでなければ$f(a,b) := \max\{a,b\}$とすると、$(M,f)$は任意の元が$\{0\}$によって生成される代数であり、有理数上の通常の順序$\le$は$A = \{0\}, F_2 = \{f\}$とした項代数の項順序とみなすことができる。
Kruskalの木定理により$M$上で$\le$は整擬順序であり、特に$\le$は全順序なので整列順序である。
すなわち、可融数全体は有理数上の通常の順序$\le$について整列する。