数理整備　無限遠点、次元概念、計算モデル拡張

無限遠点及び角の三等分線解法

無限遠点における0点同時性、曲率0かつ無限遠点解を持たない完全線超越拡大を考察する

(1)無限遠点

平行線　y=0+x　y=2+x　y=4+x　など　y=f(x)
f(x)(p∞ce)=±∞(p∞ce)=0(p∞ce)
0=0(p∞ce)$\land$0$\not\cong$0(p∞ce)
無限遠点概念拡張済 (Point at Infinity (p∞) Conceptually Extended): p∞ce
無限に遠ざかると点になる意味である、無限遠点とはユークリッド平面上の互いに平行な2直線の交点であるから、ユークリッド平面における無限遠点は上記の場合、最終的に(x, y)=(0(p∞ce), 0(p∞ce))となる点である
これは無限速量子が0,1,無限遠点による量子重ね合わせ情報を持つことを示唆する
故に、全ての直線は無間グレードにおいて無限遠点にて0点同時性を持つ

(2)実際作図の場合の解法

解法1
下記(3) MN = MG´ などを作図
概念作図ではなく実際作図では数回の動作で目標の点に辿り着くのであり、有限回操作である、有限回操作で無間点に到達したとするのが実際作図であると捉えられる
ただし、概念作図過程をみる場合は認められない
 
解法2
幾何学的に直線は半径無限大の円周と把握できるのであり、0から半径上位グレードの無間無限(円周を有限回分割しても円周率に解を出せるグレードの意味)の円周を作図するとすればよい、それが直線である(作図問題の都合上鉛筆の太さだったりある程度の誤差は許容されるので、2等分線等を駆使すればよい)
あとは直線である円周部分について三角形の重心を使って1/3を導き出せば終わりである。
直線とはいえ曲率があるのは明らかであるので、誤差を全く認めない場合は、そもそも実際の作図は全て不可能であると言っていいレベルであり、次の概念作図のみとなる

(3)概念作図の場合の解法

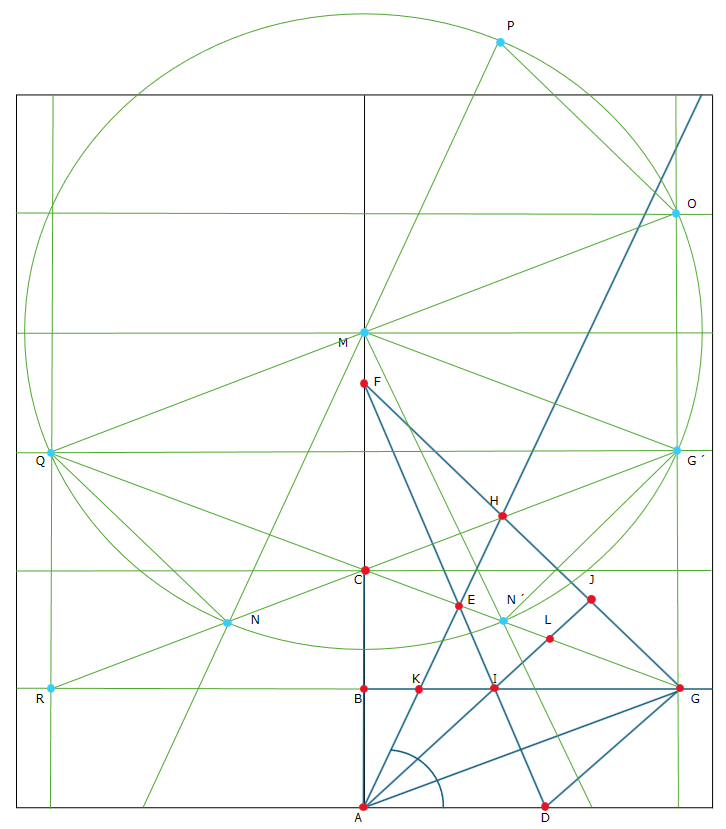角の三等分参考図
AB=BCの線を作図し、E点(DF軸)を中心にAE=EGかつCE=EHかつAC=GHとなればAI・AGが三等分線となる
なお、IJとJG(JGとGD)は直角、ADとBGは平行、FDはCH・AGの垂直二等分線、角IGA=角GADである
有限回のルールであり直線や円周は有限回の定規・コンパス使用によって描かれる必要がある

手順例(折り紙可能)
角CAH=角HGCによって角度が確定する
CAH=HGCとなる三角形を作図する
AJとHGは垂直であり、AH=AG=GC=GAかつHJ=JG=CB=BAである
角CAH=角HGCよりE点が確定する
CE=EHと、DF軸との垂直線CHよりI点が確定する
AIとAGが三等分線である

最小単位有りの場合の時点解
無間レベルでは点から進まない、点集合である線(円は不問とする)となるには有間である必要があり、かつ永続極小拡大がなく最小単位が存在するケースでは、例としてAH線上の点すべてからBK線までの円弧を描くと作図可能である(時点作成可能、二等分線など同様最小単位の余りは考慮せずとも手順のみでよいと解釈)

無限速解・無限回解
意識無限速や無限の住人には可能な解法、コンパス無限速であれば位置確定にコンパス3つを同時に使用できる意味であり、H´G´(CA)かつAH´=AG´の位置を正確に確定することが可能である、無限速でなくとも無限回の動作による位置確定であればよい、MN=MG´、G´N´=G´G(角NMA=角N´MA=角KAM)など
G´Gの縦線がわかっていれば、AC=N´G´となる線分CGを引くのみとなるなど、含みがある気もするので参考図を参照されたい

(4) まとめ

よく無限から数字を実数に持ってきて式変形する手法(無限減衰の処理はしないので、無から持ってくる→ゼロ無限算による対称性の破れである)を目にするが、念自在世界の概念界の話でよければ、任意の概算値をもって完全三等分線とするなどの回答でよい、転がして直線にして重心を使うなど
実数の公理a/a=1、1/0計算不可世界において、円周率を割り切る値は実数永続無限ではなく、上位グレードの無間無限(大きさ無限)であり、無間無限の円周を描いた場合その円周は直線であるが、その際の曲率・誤差を認めない場合は、最小単位有りの場合の時点解のみとなる

2.実数公理a/a=1、1/0計算不可世界のトポロジー次元

世界の構成要素群であり、全パターン考察する

第一次構成要素　点、線、円、球
第二次構成要素　点、線、円、球　いずれかの組み合わせ(例として、連結したまま外せないキーホルダー(円円、円同士は接触しないものとする)、ひも付きキーホルダー(線円、線円は接触するものとする))
第三次構成要素　点、線、円、球　いずれかの組み合わせ2つ
第四次構成要素　以下略
　その他、0>1かつ1>2かつ0<2、10乗すると∞になる、3つ足すと-1になる世界など、全概念全想定である

(1) 顕現群・概念群トポロジー全形態

任意の回転体につき、0次元点からみていく
・ユークリッド空間にて交わる・交わらない
・ユークリッド空間にて交わらないもの　無限遠点にて交わる・交わらない
実数公理a/a=1、1/0計算不可世界では、上記論点2-1(1)より、実数超越拡大世界の完全線はユークリッド空間では交わらなく、無限遠点にて交わると解される。
ここでいう次元は任意の一動作追加による閉連続体(循環系)群である。(2)にて後述の開連続体(非循環系)群は無限遠点視点にて点となり次元が上がるものとする
 
0次元　点①(点(みえない球(Invisible Sphere (IS))　ただし、0次元の点は－1次元からみると内部が空洞のケースが想定される、0次元視点からはみえない球(IS)、－1次元視点からは球面と表記する))
1次元　点①側　点①点②(その場別回転、速度  に別速度  追加を含む)　点①円①
2次元
点①点②側　点①点②点③(その場別回転)　点①点②円①
点①円①側　点①円①球面①　点①円①円②(その場別回転、以下略)　点①円①網円縦①(ねじれ)　点①円①網円横①(ねじれ、以下略)　点①円①トーラス①
3次元
　点①点②点③側　点①点②点③点④　点①点②点③円①
　点①点②円①側　点①点②円①球面①　点①点②円①円②　点①点②円①網円縦①　点①点②円①網円横①　点①点②円①トーラス①
　点①円①円②側　点①円①円②球面①　点①円①円②円③　点①円①円②網円縦①　点①円①円②網円横①　点①円①円②トーラス①
　点①円①網円縦①側　点①円①網円縦①球面①　点①円①網円縦①円①　点①円①網円縦①網円縦②　点①円①網円縦①網円横①　点①円①網円縦①トーラス①
　点①円①網円横①側　点①円①網円横①球面①　点①円①網円横①円①　点①円①網円横①網円縦①　点①円①網円横①網円横②　点①円①網円横①トーラス①
　点①円①トーラス①側　点①円①トーラス①球面①　点①円①トーラス①円①　点①円①トーラス①網円縦①　点①円①トーラス①網円横①　点①円①トーラス①トーラス②
　点①円①球面①側　点①円①球面①球面②　点①円①球面①トーラス①
4次元　以下略

０次元以下、球、円のみの場合は、0次元みえない球(IS)、－1次元みえない円(Invisible Circle (IC))、－2次元みえないみえない球(IS 2)、－3次元みえないみえない円(IC 2)、以下略
トーラスのみの場合は上記2次元トーラス、1次元円(みえないトーラス(本稿では円も円環(トーラス)の範疇とする。無限速においては、太さのある円環は、円→円環、円→球面と同様になるものとする)(Invisible Torus (IT)))であり、0次元点(みえない円(みえないみえないトーラス(IT 2)))、－1次元みえないみえない円(みえないみえないみえないトーラス(IT 3))、以下略。さらに、4次元、5次元と考えていくと0次元のバリエーションレベルは上がる
正多面体、正方形などの正形体、楕円体(他フラクタル・カオスなど全形体)、虚数など、その他想定可能な形状を1次元の点(みえない形)にしたものを想定、±無限次元、±0次元、±整数次元、±小数(小数点以下1桁～永続)次元などを全グレードバリエーション考える

(2)　軸次元

(1)では、任意の一動作による閉連続体郡の次元、いわゆる微積分次元を取り扱った
ここでは、軸による次元を扱う

a.軸次元例　軸増やし次元・円環等分次元

軸とは回転するものの中心となる棒(完全球完全円中心完全点上の完全線大きさ全グレード超越拡大)である
全球上で円環(円)1個ずつ増やすのか、円環で等分していくのか、両方ある

軸増やしの次元
完全球の縦横高さ軸三円環が三次元であるので、次元を増やすとはこの円環を増やす意味となる

円環等分次元
0等分全球360度、2等分半球180度、4等分1/4球90度、8等分1/8球45度、16等分1/16球22.5度、以下略

b.任意の一動作による開連続体郡の次元

よく議論されるのが、無限遠点を持たないユークリッド空間上の任意の一動作による開連続体郡の次元である
点線面体積の例(その他、0次元点、1次元螺旋など)
0次元　完全点
1次元　完全線(点集合)
2次元　完全面(線集合)
3次元　完全体積(面集合、4次元点)
4次元　(大きさ3次元体積の)線(3次元体積集合)
5次元　(大きさ4次元線の)面(4次元線集合)
6次元　(大きさ5次元面の)体積(5次元面集合)
以下略

3.$\sin$・$\cos$拡張、代数拡張

波解析例
z=2($\cos\theta$+$i\sin\theta$)
$z^{6}$=64($\cos6\theta$+$i\sin6\theta$)
$6\theta$=$0$,$2\pi$,$4\pi$,$6\pi$,$8\pi$,$10\pi$,$12\pi$(360度=0度以下略)
$\theta$=$0^{\circ}$,$60^{\circ}$,$120^{\circ}$,$180^{\circ}$,$240^{\circ}$,$300^{\circ}$
これだと、実部と虚部の複素平面しか扱えない
AI、1兆パラメータの時代に$\sin$・$\cos$による円周上の点解析のみで事足りるであろうか。AI解計算析時代、計算モデル拡張想定は当然の摂理である

(1) $\sin$・$\cos$拡張(球、トーラス、網の目、螺旋)

球面拡張　実部平面と虚部の複素球面など　単位球面上の点(ないし線など、以下略)
トーラス面拡張　単位トーラス面上の点　閉連続円環形状世界循環結晶解析
網の目拡張(円縦拡張、円横拡張、球拡張)　単位網の目円縦周上の点　単位網の目円横周上の点　単位網の目球周上の点　ボイド解析
螺旋拡張(円拡張、球拡張)　単位螺旋円上の点　単位螺旋球上の点　黄金数解析など

(2) 代数拡張(面型円型球型)

一次元的処理よりも二次元的処理の方がより並列処理性が向上すると考える
なお、一次元的でも前後から(計2方向)、前後・真ん中前後へ(計4方向)など、並列処理は可能である。

線型代数　線形空間と線形変換
面型代数　面形空間と面形変換
円型代数　円形空間と円形変換
球型代数　球形空間と球形変換