ハッピーシンセサイ算~一次方程式は算数で解ける~
問題
早速問題です。
$ \mathrm{AB} /\!/ \mathrm{CD}, \mathrm{AB} \perp \mathrm{AC} $とし、$ \mathrm{AD} $と$ \mathrm{BC} $の交点を$ \mathrm{E} $、$ \mathrm{E} $から$ \mathrm{AC} $に下ろした垂線の足を$ \mathrm{F} $とする。
$ \frac{\mathrm{CD}}{\mathrm{AC}} = m_1, \frac{\mathrm{AB}}{\mathrm{AC}} = m_2, \mathrm{AB} = a $とするとき、$ \mathrm{AF} $を$ m_1, m_2, a $で表せ。また、それを算数の範囲で証明せよ。
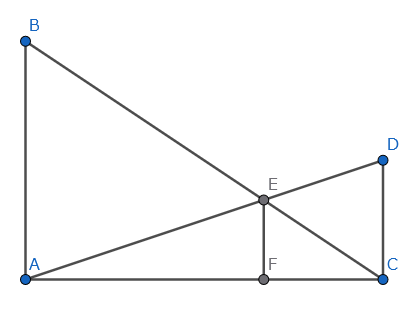
めろちんさんのハッピーシンセサイザの振り付けにこの図に似た箇所があるので[1]、私はこれをハッピーシンセサイ算と呼んでいます。
横軸を時間軸に見立てる。
$ \mathrm{A} $を出発して$ \mathrm{B} $に速さ$ m_1 $で向かう点$ \mathrm{P} $と、それと同時に$ \mathrm{B} $を出発して$ \mathrm{A} $に速さ$ m_2 $で向かう点$ \mathrm{Q} $を考える。
$ \mathrm{P} $と$ \mathrm{Q} $が出会うのは出発から$ \frac{a}{m_1 + m_2} $が経過したときであり、それが$ \mathrm{AF} $の長さに等しい。
点$ \mathrm{P} $が動くことで一瞬で解けてしまいました。点$ \mathrm{P} $動け。
$ \mathrm{CD} $上に$ \mathrm{C'} $を取り、$ \mathrm{BC'} $と$ \mathrm{AD} $の交点を$ \mathrm{E'} $、そこから$ \mathrm{AC} $に下ろした垂線の足を$ \mathrm{F'} $とする。
$ \mathrm{BC'} $の傾きを$ -m_1' $とすれば、$ \mathrm{AF'} = \frac{a}{m_1' + m_2} $である。
「解答」の議論を追うことで即座に分かります。
応用
別の形も解いてみましょう。設定は前の問題と似ていますが、$ \mathrm{AB} \perp \mathrm{CD} $になっています。
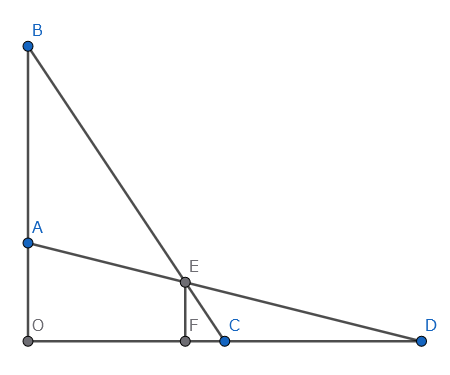
$ \frac{\mathrm{BO}}{\mathrm{OC}} = m_1, \frac{\mathrm{AO}}{\mathrm{OD}} = m_2, \mathrm{AB} = a $とすれば、上と同様の考察により$ \mathrm{OF} = \frac{a}{m_1 - m_2} $がわかります。
結論
点$ \mathrm{P} $動け。