平方根の近似値を求める方法をたくさん紹介して、最速を決める。
平方根の近似値を求める方法をたくさん紹介して、最速を決める。
選手紹介
$\sqrt5$を例にそれぞれ見ていきましょう。
操作の難易度を大まかに学年で表しています。
1.暗記する(小学生~)
語呂合わせで覚えてしまいしょう。
概念すら知らなくても暗記はできるので小学生でも可。
小数点以下数桁までなら最速です。
例)富士山麓オウム鳴く $\sqrt5=2.2360679...$
2.二分探索ごり押し(中学生~)
二乗して比較を繰り返し、範囲を半分に半分にしていきます。
10回やれば3桁求まる?
例)$2 \lt \sqrt5 \lt 3$
$\frac{2+3}2=\frac52 \gt \sqrt5$より、$2 \lt \sqrt5 \lt \frac52$
同じ操作を繰り返す
3.開平法(中学生~)
みなさん聞いたことはあると思います。
計算すればするほど面倒になっていきます。
説明は長くなるので割愛します。
4.アナログに作図する(中学生~)
正確に90度が測れたり、長さを測る術があるのならばできないことはありません。
例)辺の長さが$1,2,\sqrt5$の直角三角形を作図します。
メモリの最小単位の$\frac1{10}$まで見るのは理科の基本です。
$\sqrt5$は大体$2.21$という結果を得ました。
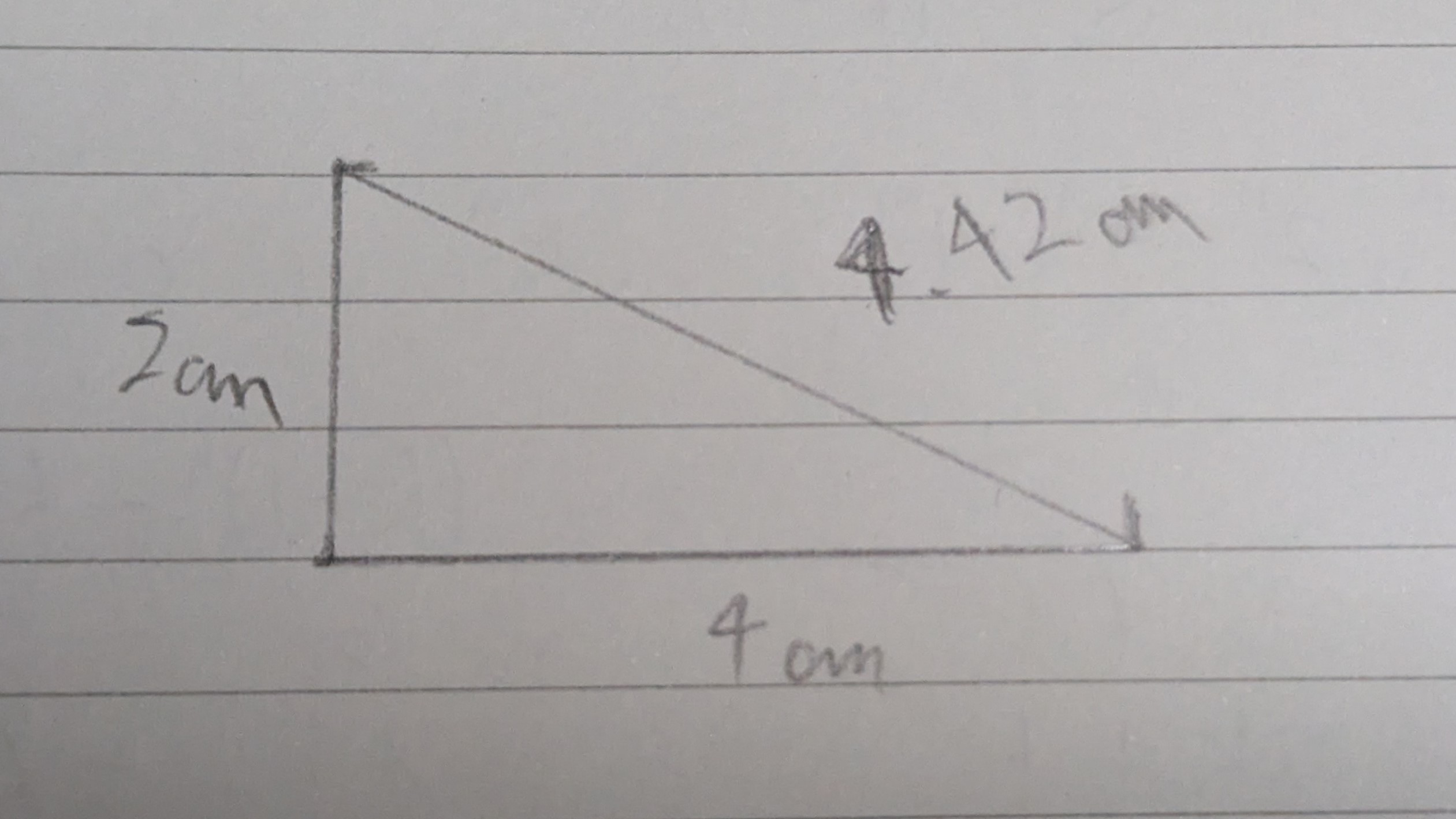 mathlog内でアナログな画像はなかなか見ない
mathlog内でアナログな画像はなかなか見ない
5.連分数表示(中学生~)
小数部分を求めるような形にして、分子の有理化を行うとできます。
例)$\sqrt5-2=\frac1{2+\sqrt5}$よって$\sqrt5=2+\frac1{2+\sqrt5}$
この式の右辺の$\sqrt5$にまた式を代入すると
$\sqrt5=2+\frac1{4+\frac1{4+...}}$となる。
途中で打ち切り$2+\frac1{4+\frac14}$を計算すると
$\frac{38}{17}=2.2352941...$
6.ニュートン法(高校生~)
f(x)=0の解が平方根となるグラフを描き
適当に$x_0$(正の数で始めると、正の平方根が求まる)を決め、$x=x_0$のグラフの接線と$x$軸との交点を次の$x_1$とする、を繰り返していくと、$x_n$は平方根に近づいていく。
$\sqrt{D}$を求めたいとき$f(x)=x^2-D$
ニュートン法の定義は$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$なので、
$x_{n+1}=\frac12(x_n+\frac{D}{x_n})$←これを繰り返す
例)D=5で√5を求める
$x_0=2$とすると、$x_1=\frac12(2+\frac{5}{2})=\frac94$
$x_2=\frac12(\frac94+\frac{5}{\frac94})=\frac{161}{72}=2.236111...$
$x_n$とおかずに既約分数$\frac{a_n}{b_n}$とおくと$\frac{a_{n+1}}{b_{n+1}}=\frac{a_n^2+Db_n^2}{2a_nb_n}$となる。
7.ペル方程式(高校生~)
整数$x,y$に対する$x^2-Dy^2=1$なる不定方程式をペル方程式と呼びます。
式変形すると$\frac{x}{y}=\sqrt{D+\frac1{y^2}}$となり、整数解$x,y$を求めることにより$\sqrt{D}$の近似値を求めることができます。
ペル方程式には面白い性質があり
$x,y$が自然数のうち最小の解を$(x_0,y_0)$とすると、
それより大きい$x,y$のすべての整数解は$x+\sqrt{D}y=(x_0+\sqrt{D}y_0)^n$に$n=2,3,4,...$を入れたものである。
例)$D=5$として求める。
$x^2-5y^2=1$を満たす最小の解$(x_0,y_0)=(9,4)$である。
$(9+4\sqrt5)^2=161+72\sqrt5$より、$(161,72)$もまた、ペル方程式を満たす。
$\frac{x}{y}=\frac{162}{72}=2.236111...$
このまま$x_{n+1}+\sqrt{d}y_{n+1}=(x_n+\sqrt{d}y_n)^2$を行って計算を続ける場合、
$\frac{x_{n+1}}{y_{n+1}}=\frac{x_n^2+Dy_n^2}{2x_ny_n}$であり、ニュートン法の時と一致する。
平方根を求めるうえでは、同じものだと考えることができる。
8.マクローリン展開(高校生~)
$f(x)=\sqrt{1+x}$を展開して求める。
$\sqrt5$なら$2\sqrt{1+\frac14}$に、$\sqrt7$なら$3\sqrt{1-\frac29}$と$\left| x \right|\lt1$となるように調整します。
展開すると、
$\sqrt{1+x}=1+\frac{x}{2}-\frac{x^2}{8}+\frac{x^3}{16}-...$
展開の時点で少しめんどくさいです。
...の部分の項から綺麗ではないので、代入しやすいのはここまでです。
例)$\sqrt5=2\sqrt{1+\frac14}$を求める。
$x=\frac14$として、三次の項まで計算すると
$2(1+\frac18-\frac1{128}+\frac1{1024})=2.236328...$
9.おまけ(フィボナッチ数列を用いて$\sqrt5$のみ)
フィボナッチ数列の並んだ二項間比$\frac{F_{n+1}}{F_n}$は$n$が大きくなるにつれて
黄金数$φ=\frac{1+\sqrt5}2$に近づいていく。
例)フィボナッチ数列を書き出す$1,1,2,3,5,8,13,21,34,55,89,...$
$\frac{89}{55}×2-1=2.23636...$
最速は?
いろいろ自分の手で試した結果、
簡単な操作で値がすごい勢いで増えるニュートン法(ペル方程式)がよかったです。
ですが、これで終わりではありません。
わざわざ下から積み重ねていくのは面倒だよね?
どうせなら一発で精度の高い近似を得たいよね?
さらにその先へ(改造)
ペルの方程式の最小解$(x_0,y_0)$は求まっているものとします。
$a_1=x_0$ $b_1=y_0$ $a_{n+1}=a_n^2+Db_n^2$ $b_{n+1}=2a_nb_n$
を解いていきます。
おぞましい漸化式ですが、ニュートン法やらの計算から
$a_{n+1}+\sqrt{D}b_{n+1}=(a_n+\sqrt{D}b_n)^2$
$a_{n+1}-\sqrt{D}b_{n+1}=(a_n-\sqrt{D}b_n)^2$
から
$a_n+\sqrt{D}b_n=(x_0+y_0\sqrt{D})^{2^{n-1}}$と$a_n-\sqrt{D}b_n=(x_0-y_0\sqrt{D})^{2^{n-1}}$が得られ、公式を得る。
$a_n=\frac12((x_0+y_0\sqrt{D})^{2^{n-1}}+(x_0-y_0\sqrt{D})^{2^{n-1}})$
$b_n=\frac1{2\sqrt{D}}((x_0+y_0\sqrt{D})^{2^{n-1}}-(x_0-y_0\sqrt{D})^{2^{n-1}})$
...失敗しました。
こんなのに代入するぐらいなら、さっきの漸化式を使って進めていったほうがはるかに楽です。申し訳ございませんでした。
実践!!!!
$√5の近似値を求めよ。(実際の値と小数第n位まであっていた時n点を与える)$
ペル方程式ニュートン法と漸化式の合わせ技で解く。
初期値を$2=\frac21$とすると、
$a_1=2$$ $$b_1=1$となり、
$a_{n+1}=a_n^2+5b_n^2$ $b_{n+1}=2a_nb_n$を用いると、
| n | a_n | b_n |
|---|---|---|
| 1 | 2 | 1 |
| 2 | 9 | 4 |
| 3 | 161 | 72 |
| 4 | 51841 | 23184 |
| 5 | 5374978561 | 2403763488 |
| 6 | 57780789062419261441 | 25840354427429161536 |
疲れたのでここまで、
$\frac{a_n}{b_n}$で近似できることは覚えていますか?
$\frac{57780789062419261441}{25840354427429161536}$
$=2.236067977499789696409173668731276235440953...$
$\sqrt5$
$=2.236067977499789696409173668731276235440618...$
$39$点といったところでしょうか?
ちなみに$n=2,3,4,5$の場合の点数は
それぞれ$1,3,9,19$点でした。
もう2回ぐらい頑張れば100点超えそうですね。
最後に
ここまで読んでくださりありがとうございました。
他にも近似の方法があったら教えてください。
精度が悪くても、特定の場合(9.おまけのフィボナッチ数列を用いた方法のような)のものでも大歓迎です!
