無限冪であそぼ
寝覚
突然ですが、この数式、$ i$の無限冪の計算結果はどれくらいの値になると思いますか?
$$ i^{i^{i^{{\cdot}^{{\cdot}^{\cdot}}}}}$$
大体どのくらいになりそうですか?
では実際に計算してみましょう、と言いたいところですが、複素数は条件が複雑なので、まずは正の実数$x(\neq 1)$ の無限冪から考えてみましょう。
🆗
正の実数$x(\neq 1)$ の無限冪
$$ x^{x^{x^{{\cdot}^{{\cdot}^{\cdot}}}}}$$
この極限が「ある一定の値yに収束する」とすると、
$$ x^{x^{x^{{\cdot}^{{\cdot}^{\cdot}}}}}=y$$
この冪塔は無限に続いていくので、指数部分も同様に$ y$へと収束すること、
つまり$y=x^y$が成り立ちます。(逆は成り立たない(後述))
漸化列$y_{n+1}=x^{y_n},y_1=x$の極限$$\lim_{n\to\infty}y_n$$ がここでいう無限冪の極限$y$に相当する
これを変形すると、
$$ \ln y=y \ln x$$
$$ \ln y=e^{\ln y} \ln x$$
$$(\ln y )e^{-\ln y}=\ln x $$
$$(-\ln y )e^{-\ln y}=-\ln x $$
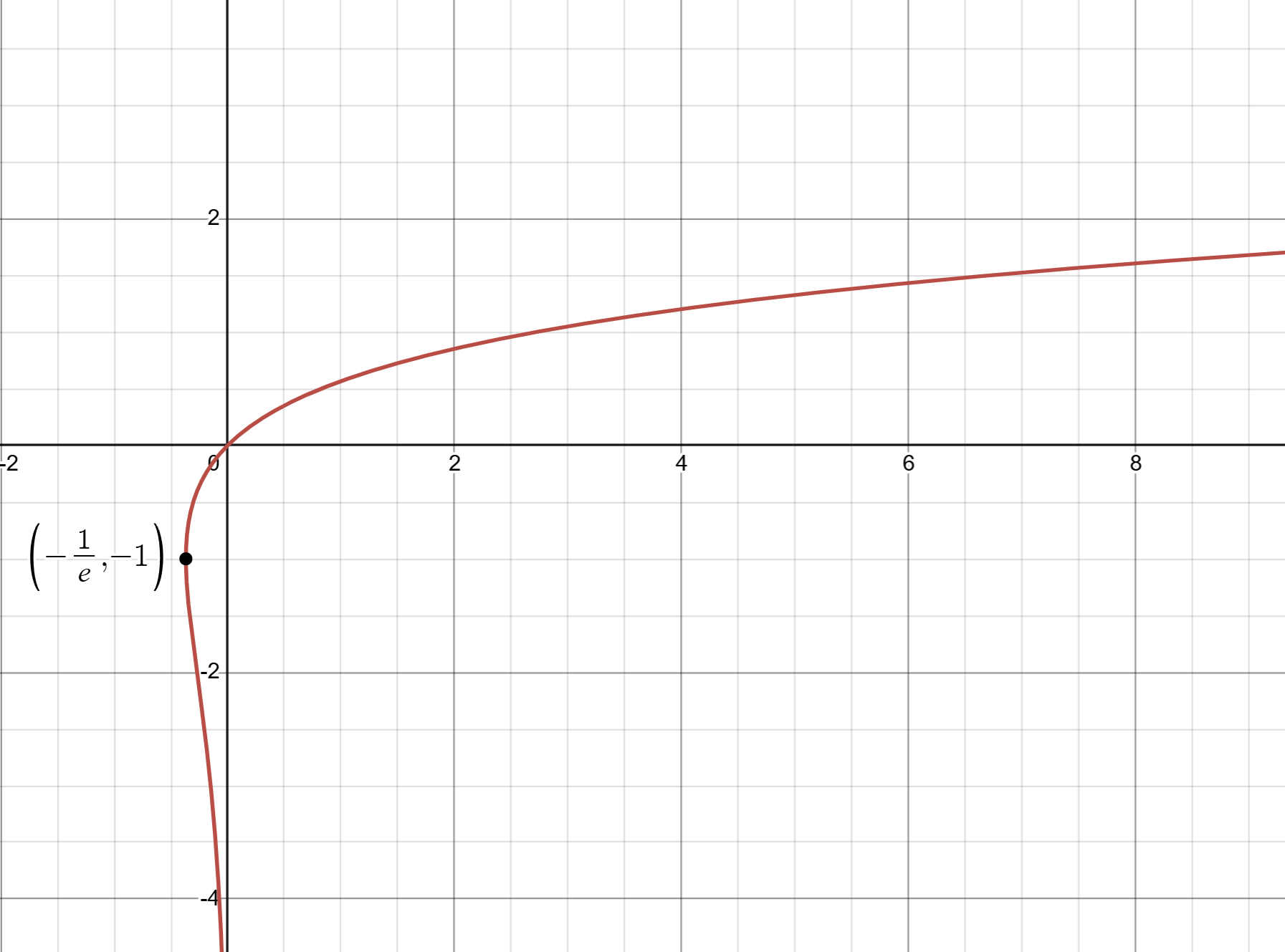
ここで、以下のように定義される多価性のある超越関数「ランベルトのW関数」を導入します。
$$ W(z)e^{W(z)}=z $$
 LambertW1
LambertW1
このランベルトのW関数を用いれば、数式はさらにこのように変形できます。
$$ -\ln y=W(-\ln x)$$
$$ \ln y=-W(-\ln x)$$
$$ y=e^{-W(-\ln x)}$$
($we^w=z \Leftrightarrow w=W(z)$から)
$$ y=-\frac{W(-\ln x)}{\ln x}$$
$y=f(x)$の形に辿りつきました。$ W(-\ln x)$の値がわかれば$y$、つまり無限冪の収束値の候補もわかりますね。
たとえば$x=\sqrt2$の無限冪$ \sqrt{2}^{\sqrt{2} ^{\sqrt{2} ^{{\cdot}^{{\cdot}^{\cdot}}}}}$を求めたいなら
$$ y=-\frac{W(-\ln\sqrt{2})}{\ln \sqrt{2}}$$
$$y=-\frac{2 W(-\frac{\ln 2}{2})}{\ln 2} $$
$ W(-\frac{\ln 2}{2})=W(-\ln\sqrt{2})$の値を知りたいです。
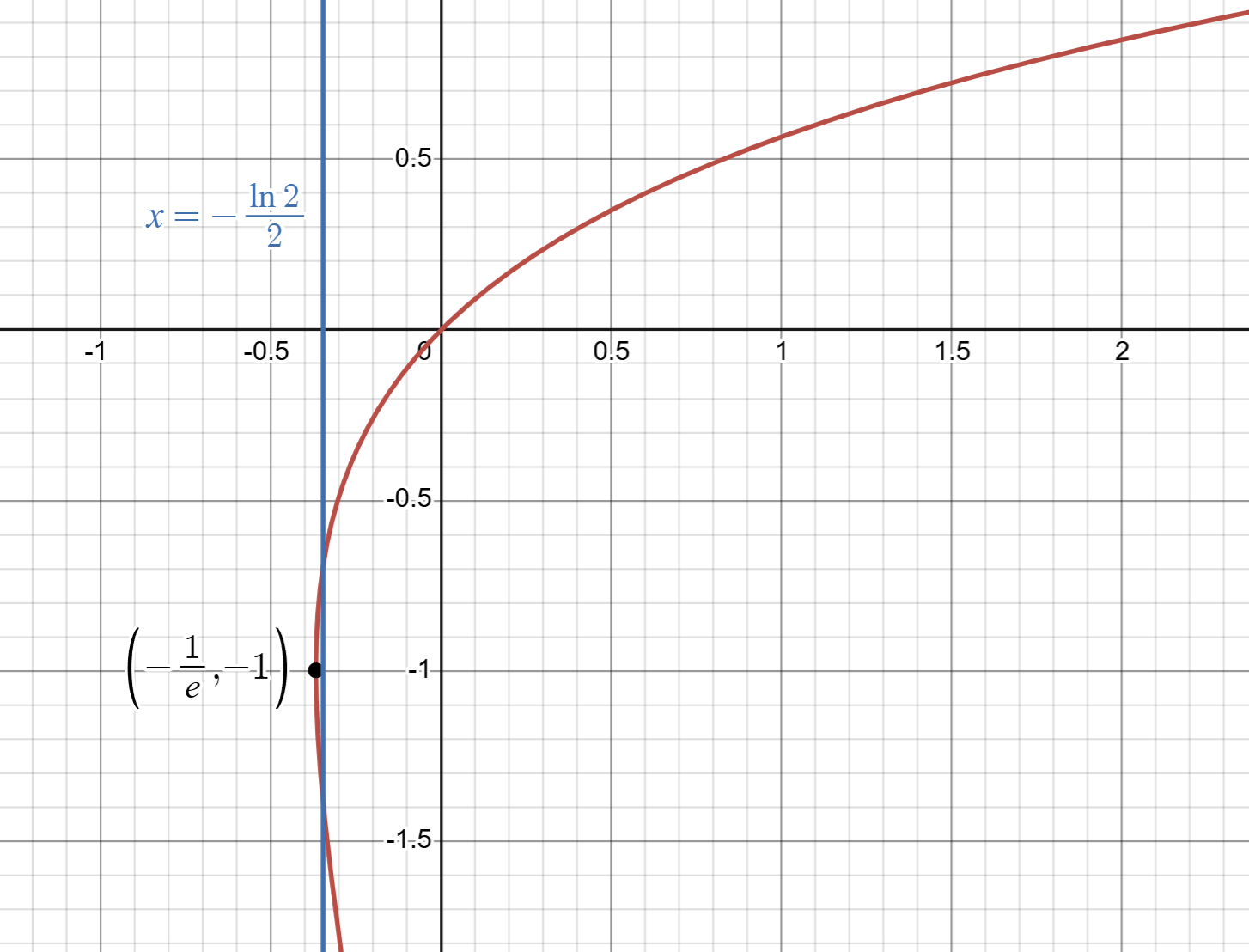
Wのグラフを見てみましょう。
 LambertW2
LambertW2
最初に言った通りWは多価関数なので交点が2つありますね。
($W(x) \geq -1$の部分を「主枝」$W_0(x)$とすれば1価です。グラフの主枝でない部分は分枝$W_{-1}(x)$です。)
グラフを見て整理してみましょう。
| 引数の大きさ | W(x)のとる実数値の数 |
|---|---|
| $x\lt -\frac{1}{e}$ | $0 $ |
| $x=-\frac{1}{e}$ | $1$ |
| $ -\frac{1}{e}\lt x \lt 0$ | $2$ |
| $x\geq0$ | $1$ |
$-\frac{1}{e}\approx-0.367879441171$だから、いま($-\frac{\ln 2}{2}\approx -0.34657359028$)は$ -\frac{1}{e}\lt x \lt 0$です。
$ W(-\frac{\ln 2}{2})$は2つの値、具体的には$ -\ln 2$と$ -\ln 4$の2つをとります(簡単な式で表せているのは激レアで、ふつうはWより簡単にできたりはしない)。
つまり収束先$y$は
$$y=-\frac{2 W(-\frac{\ln 2}{2})}{\ln 2} =2,4$$
の2つをとります。
実際、$ 2=\sqrt{2}^2$、$ 4=\sqrt{2}^4$なのでこれは厳密に正しい解です。
さらに複素範囲まで考えれば、$ W(-\frac{\ln 2}{2})$は無限個の値をとります。その例の1つとして、分枝の1つ$W_2$で考えれば、$W_2(-\frac{\ln 2}{2})\approx-3.7245326355744 + 13.8749129742688 i $で、このときの$y_2\approx 10.7467295259446 - 40.0345362814872 i$も実際に$y_2=\sqrt{2}^{y_2}$を満たします。
どれが無限冪の「真の収束値」を得るものでしょうか。
さきほどスルーした「ある一定の値$ y$に収束」の条件について、実はこのような条件が知られています1。
| $x$の値 | 不動点の値 | 不動点数 | 漸近時のふるまい |
|---|---|---|---|
| $ x>e^{1/e}$ | - | 0 | $+\infty$に発散 |
| $x=e^{1/e}$ | $y=e$ | 1 | $y$に収束 |
| $1< x< e^{1/e} $ | $ 1< y< e$ | 2($W_0$と$W_{-1}$に1つづつ) | $W_0$の安定解$y$に収束 |
| $ x=1$ | $y=1$ | 1 | ずっと$1$ |
| $e^{-e}< x<1$ | $1/e< y< e$ | 1 | 振動して$y$に収束 |
| $x=e^{-e}$ | $y=1/e$ | 1 | 振動して$y$に収束 |
| $0< x< e^{-e}$ | $0< y_1<1/e< y_2<1$ | 不安定な1(2サイクル) | 2サイクルに収束 |
| $x\to 0^{+} $ | $y_1\to0, y_2\to1$ | 不安定な1(2サイクル) | 2サイクルに収束 |
$e\approx2.71828$$e^{1/e}\approx1.44467$$1/e\approx0.367879$$e^{-e}\approx0.065988$
実際に確認してみれば、たしかに無限冪としての正しい収束値は1つめ(主枝$W_0$)を採用した$y=2$のほうであることがわかりますね。
$ \sqrt{2}^{\sqrt{2} ^{\sqrt{2} ^{{\cdot}^{{\cdot}^{\cdot}}}}}=2$
![!FORMULA[88][1762842122][0]の無限冪](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fsa9pKgKucMvR4alj0O4q.png?alt=media) $\sqrt2$の無限冪
$\sqrt2$の無限冪
![!FORMULA[89][1762842122][0]の無限冪](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F4DG5wbQRqhdFWcBbe5lV.png?alt=media) $\sqrt2$の無限冪
$\sqrt2$の無限冪
$$ x^{x^{x^{{\cdot}^{{\cdot}^{\cdot}}}}}$$
これが「ある一定の値yに収束した」とすると、
$$ x^{x^{x^{{\cdot}^{{\cdot}^{\cdot}}}}}=y$$
xの冪乗は無限に続いていくので、xのy乗もyであること、つまり、yイコールxのy乗が成り立ちます。
$$ y=x^y$$
「$ y $が方程式$ y=x^y $を満たす」は必要条件にすぎないということです。
$y=x^y$を満たすからといって安定収束な無限冪の極限になるわけではありません。$y$はあくまで候補(不動点)です。
ほかの無限冪も見てみましょう。
0.5の無限冪なら、同様にして、その収束値はおよそ0.6412くらいになります。
$$ 0.5^{0.5^{0.5^{{\cdot}^{{\cdot}^{\cdot}}}}}=-\frac{W(-\ln 0.5)}{\ln 0.5}\approx 0.64118574450498598448$$
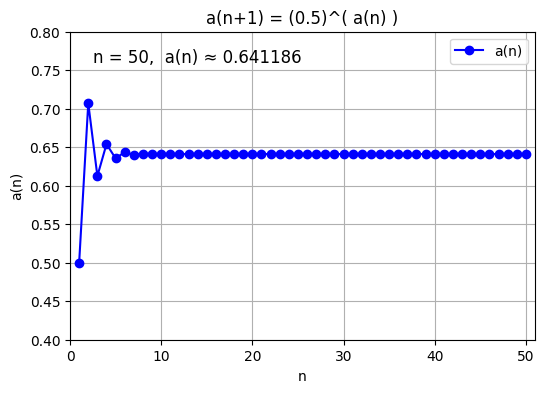 0.5無限冪
0.5無限冪
0.05なら、2サイクル(周期2軌道)で振動=2点を行き来する収束をします。
$$ 0.05^{0.05^{0.05^{{\cdot}^{{\cdot}^{\cdot}}}}}$$
その収束値は
$$ y=-\frac{W(-\ln 0.05)}{\ln 0.05}\approx 0.350224852743194$$
ではなく
$y=0.05^{0.05^y}$すなわち$\ln y=0.05^y\ln 0.05$
の解のうち適切な2つの実数解$y_1,y_2$が2サイクルの収束値になります。(例の公式$ y=-\frac{W(-\ln x)}{\ln x}$は1サイクル用で、いま、不安定な1サイクルは消滅する:周期倍分岐period-doubling bifurcation →2サイクルが安定になる)
具体的には、反復が奇数回のとき$y_1\approx 0.137359395737956 $に、奇数回のとき$y_2\approx 0.662660838900548 $に収束します。
$$ \underbrace{0.05^{0.05^{0.05^{{\cdot}^{{\cdot}^{\cdot}}}}}}_{反復がm回}=\begin{eqnarray}
\left\{
\begin{array}{l}
\mathrm{if}\;m \equiv1\:(\mathrm{mod}\: 2) \:y_1\approx 0.137359395737956 \\
\mathrm{if}\;m \equiv0\:(\mathrm{mod}\: 2) \:y_2\approx 0.662660838900548
\end{array}
\right.
\end{eqnarray}$$
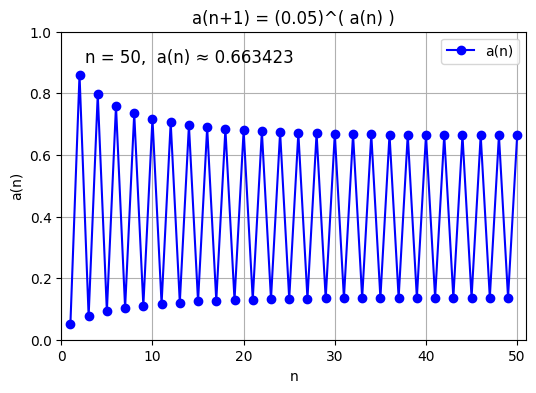 0.05無限冪
0.05無限冪
厳密解を示したかったら新しく関数を定義する必要がありますね。
$$ W^{(2)}(z)e^{W^{(2)}(z)e^{W^{(2)}(z)}}=z $$みたいな?
ほかの問題
余談ですが、ランベルトのW関数を使えば、$ y=e^x$と$y=x+2 $の交点も求めることができますね
$$ x+2=e^x$$
$$(x+2)e^{-x}=1$$
$$(x+2)e^{-(x+2)}=e^{-2}$$
$$-(x+2)e^{-(x+2)}=-e^{-2}$$
$$-(x+2)=W\left(-e^{-2}\right) $$
$$x=-W\left(-e^{-2}\right)-2$$
これが厳密解です。近似解は
$$x\approx-1.84141,\:1.14619$$
($W_{0}$と$W_{-1}$)
![!FORMULA[119][-805828929][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FpdHfAMmg1gZ6oSMmzle0.png?alt=media) $ x+2=e^x$
$ x+2=e^x$
iの無限冪
では、本題の「iの無限冪」に戻りましょう。
正の実数$x$のとき$\ln x$は一価でしたが、複素対数では$ \ln i$が以下のような多価関数になります。
$$ \ln i=\ln|i|+i \arg i=i\left(\frac{\pi}{2}+2\pi k\right)$$
よって冪乗$i^y$は
$$ i^y=e^{y \ln i}=e^{iy (\frac{\pi}{2}+2\pi k)}$$
です。$ k \in \mathbb{Z}$によって無限個の値を持ちます。
だから、もし$i $の無限冪が収束して一定値$y$をとるのなら、実数の時と同様の議論を通して、
$$ y=-\frac{W(-\ln i)}{\ln i}$$
$$ y=-\frac{W(-i(\frac{\pi}{2}+2\pi k))}{i(\frac{\pi}{2}+2\pi k)}$$
の解を得ることになります。
(変形)
$$ y=\frac{iW\left(-i(\frac{\pi}{2}+2\pi k)\right)}{\frac{\pi}{2}+2\pi k} $$
対数の主値をとるなら$ k=0$として
$$ y=\frac{iW\left(-\frac{\pi i}{2}\right)}{\frac{\pi}{2}} $$
$$ y=\frac{2iW(-\frac{\pi i}{2})}{\pi} $$
です。
Wも多価関数でした。ここでさらにWの主枝(主値の分枝)$W_0$をとるなら
$$ W_0\left(-\frac{\pi i}{2}\right)\approx0.566417330285464 - 0.688453227107702 i$$
よって
$$ y\approx 0.438282936727032 + 0.360592471871385 i$$
つまり、主値をとりつづけたとき、
$$ i^{i^{i^{{\cdot}^{{\cdot}^{\cdot}}}}} \approx 0.438282936727032 + 0.360592471871385 i$$
が収束値の候補です。(ほかの分枝をとれば値は変わる、無限個ある)
ただ、まだ$y=i^y$の解が無限個求まっただけです。本当に主値をとった場合に収束していくのかはわかりません。複素数無限冪の収束性は複雑で、そもそも$y$に相当する極限値が存在しないだとか、途中で分枝の飛び越えなどが発生する(引数が範囲から飛び出してしまったとか)だとかも全然あり得る挙動の範囲内です。
数値実験で実際に確認してみましょう。
 iの無限冪
iの無限冪
 iの無限冪
iの無限冪
それっぽいですね。
それっぽいですが、まだ「確からしい不動点の候補が明確に極限値であることの証明」はできていません。
吸引的不動点の性質$|f'(y_0)|<1$を用いて安定性を解析します。
$$f(y)=i^y=e^{y\ln i}\overset{主値}{=}e^{y\frac{i\pi}{2}}$$
$$f'(y)=\frac{d}{dy}\left(e^{y\frac{i\pi}{2}}\right)=\frac{i\pi}{2}e^{y\frac{i\pi}{2}}=\frac{i\pi}{2}i^y$$
$$|f'(y)|=\left|\frac{i\pi}{2}e^{y\frac{i\pi}{2}}\right| $$
($y=y_0$を代入)
$$|f'(y_0)|=\left|\frac{i\pi}{2}i^{y_0}\right| $$
($ y_0=i^{y_0}$)
$$|f'(y_0)|=\left|\frac{i\pi}{2}y_0\right|=\frac{\pi}{2}|y_0|$$
($|y_0|\approx|0.4382829367 + 0.3605924719 i|\approx0.5675551633$
$\frac{\pi}{2}|y_0|\approx 0.891513565$から)
$$|f'(y_0)|=\frac{\pi}{2}|y_0|<\frac{\pi}{2} \cdot0.56756<0.89152<1$$
したがって、$$y_0=\frac{2iW_0(-\frac{\pi i}{2})}{\pi}\approx0.4382829367 + 0.3605924719 i$$は$|f'(y_0)|<1$を満たす正しい収束値である。といえます。
🆗
というわけで、$i$の無限冪
$$ i^{i^{i^{{\cdot}^{{\cdot}^{\cdot}}}}}$$
は「主値をとれば」安定的な不動点
$$ \frac{2iW_0(-\frac{\pi i}{2})}{\pi} $$
へ収束し(いま他の候補値はない)、その大体の値は
$$ i^{i^{i^{{\cdot}^{{\cdot}^{\cdot}}}}} \approx 0.438282936727032 + 0.360592471871385 i$$
ということがわかりました。
おしまい。(数値計算ライブラリが対数計算の過程で主値を採用しているなどするため、数値実験でこの値になったからといって一般にそうとは言えない、別の分枝の値をとる計算機なら別の収束値を得る)
おまけ
複素数の無限冪の収束条件について、
収束するなら黒、発散するなら白でプロットしてみたらこんな感じになりました。
![収束テスト:「パラメータ!FORMULA[158][38414][0]によって定まる反復写像
!FORMULA[159][-1170660869][0] が収束・発散する領域を可視化したもの」](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FCrmQHgbHoN0ranQpvcmm.png?alt=media) 収束テスト:「パラメータ$z$によって定まる反復写像
収束テスト:「パラメータ$z$によって定まる反復写像
$w_{n+1}=z^{w_n}$ が収束・発散する領域を可視化したもの」
「頭部」っぽくていいね
おまけ2
逆に、無限に冪乗した結果が$ i$になる$x$について考える
$$ x^{x^{x^{{\cdot}^{{\cdot}^{\cdot}}}}}=y$$
収束先の一定値$y$が存在するなら
$y=x^y$$ i.e.$$x=y^{1/y}$
だから主値をとれば
$$x=i^{1/i}=e^{-i \ln i}=e^{ (\frac{\pi}{2}+2\pi k)}=e^{\pi/2}$$
よって
$$ (e^{\pi/2})^{(e^{\pi/2})^{(e^{\pi/2})^{{\cdot}^{{\cdot}^{\cdot}}}}}=i$$
おや?実数の実数乗が(実数でない)複素数になってしまいました
主値をとらずとも$e^{ (\frac{\pi}{2}+2\pi k)}$で実数
($e^{\pi/2}\approx 4.81047738 $で、$y=x^y$に置き換えるときの「収束先$y$の存在」を満たしていない)
これ「-1/12」っぽくて良くないですか?
