【和訳】Fontene's Theorems の主張と証明

246

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

　8割くらい自分用の備忘録みたいなものです．

　タイトルより多い情報は載っていません．
　エアプなのでいろいろ汚いと思います．
　必要知識はないです（船旅1~4章？）

第一フォントネーの定理

Fontene's First Theorem

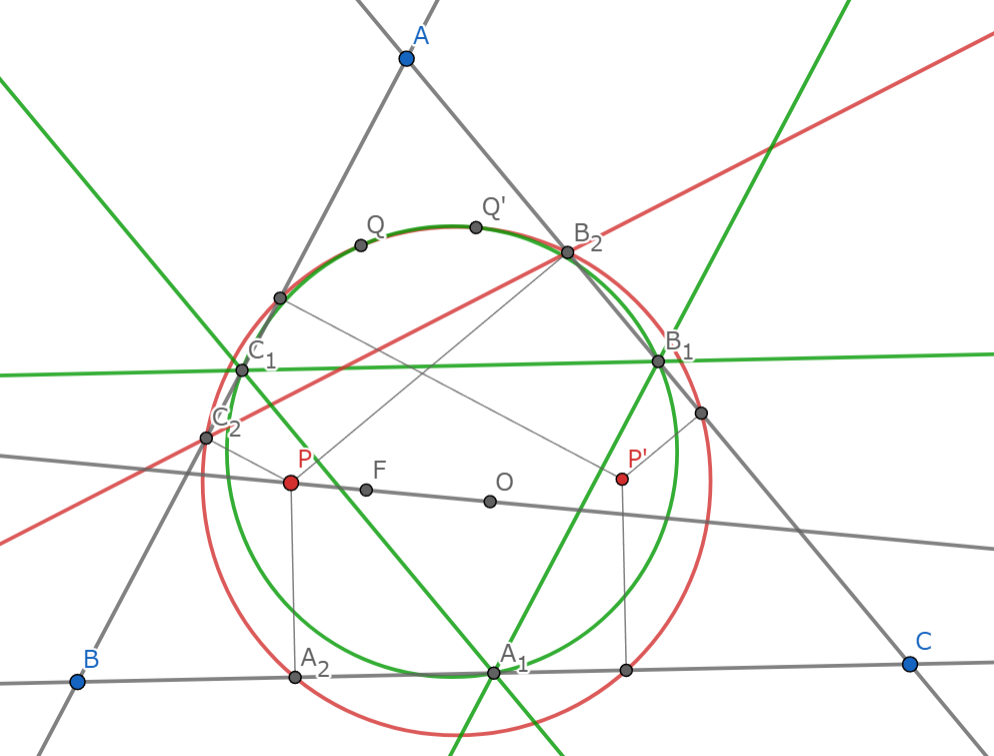
　三角形$ABC$と点$P$について，その中点三角形を$\triangle A_1B_1C_1$とし，$P$の垂足三角形を$\triangle A_2B_2C_2$とする．直線$B_1C_1$と直線$B_2C_2$の交点を$X$，直線$A_1C_1$と直線$A_2C_2$の交点を$Y$，直線$A_1B_1$と直線$A_2B_2$の交点を$Z$とすると，3直線$A_2X,B_2Y,C_2Z$および2円$(A_1B_1C_1),(A_2B_2C_2)$は1点で交わる．

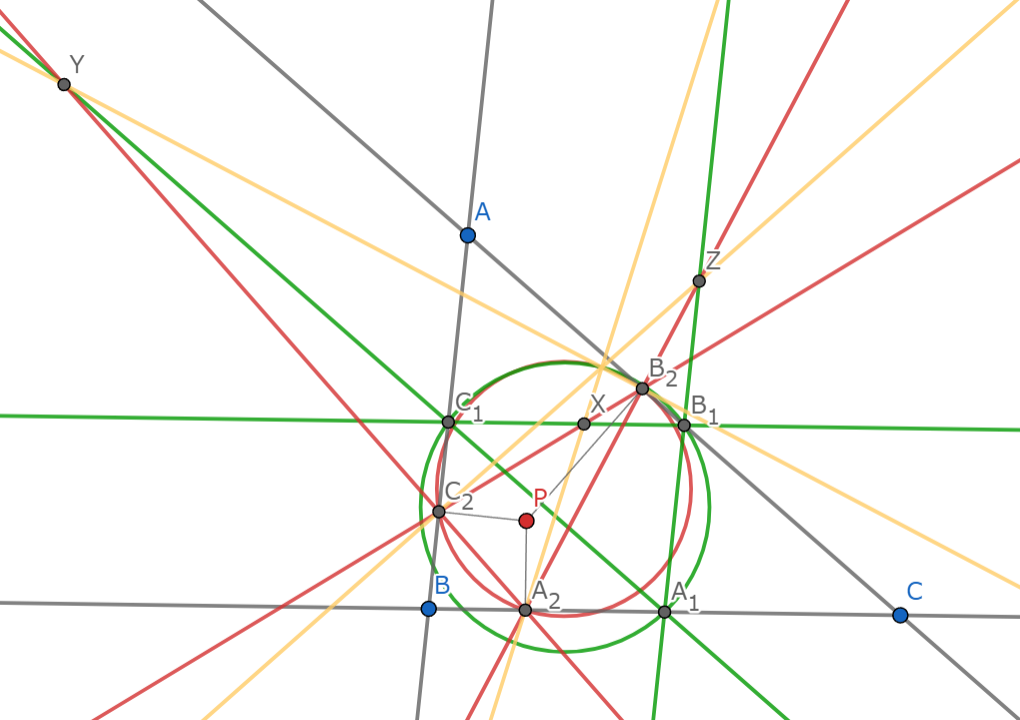主張は黄の共点

　$(ABC),(A_1B_1C_1),(A_2B_2C_2)$の中心をそれぞれ$O,E,O'$とする．

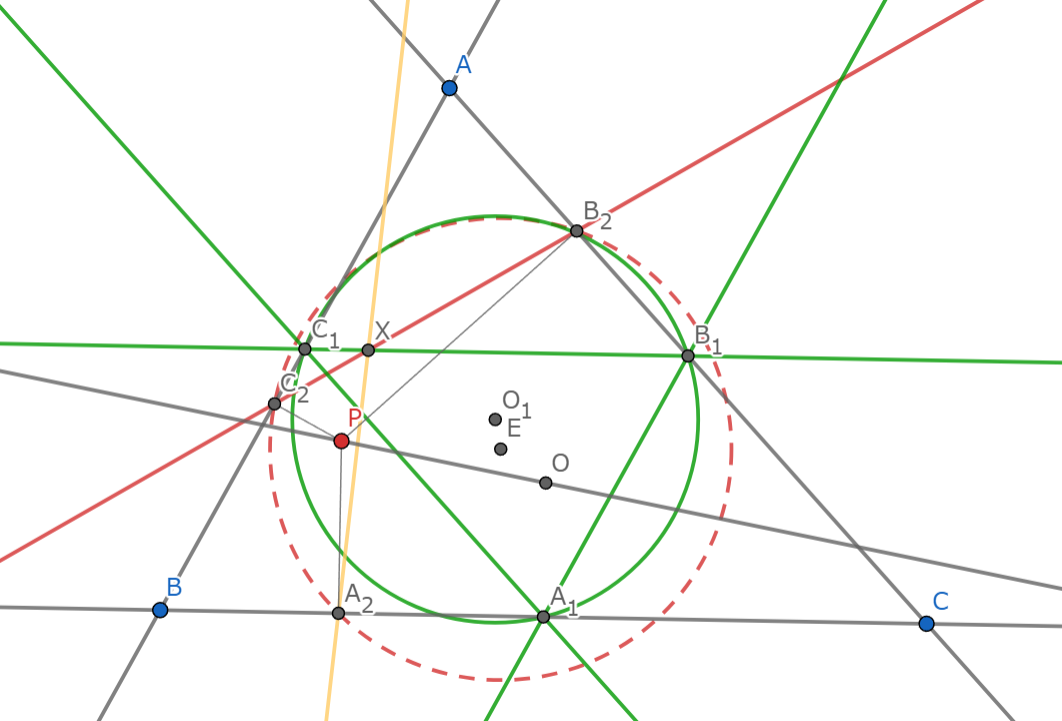
　$A$から直線$OP$に降ろした垂線の足を$F$とし，$A_2$を$B_1C_1$に関し対称移動した点を$L$とする．

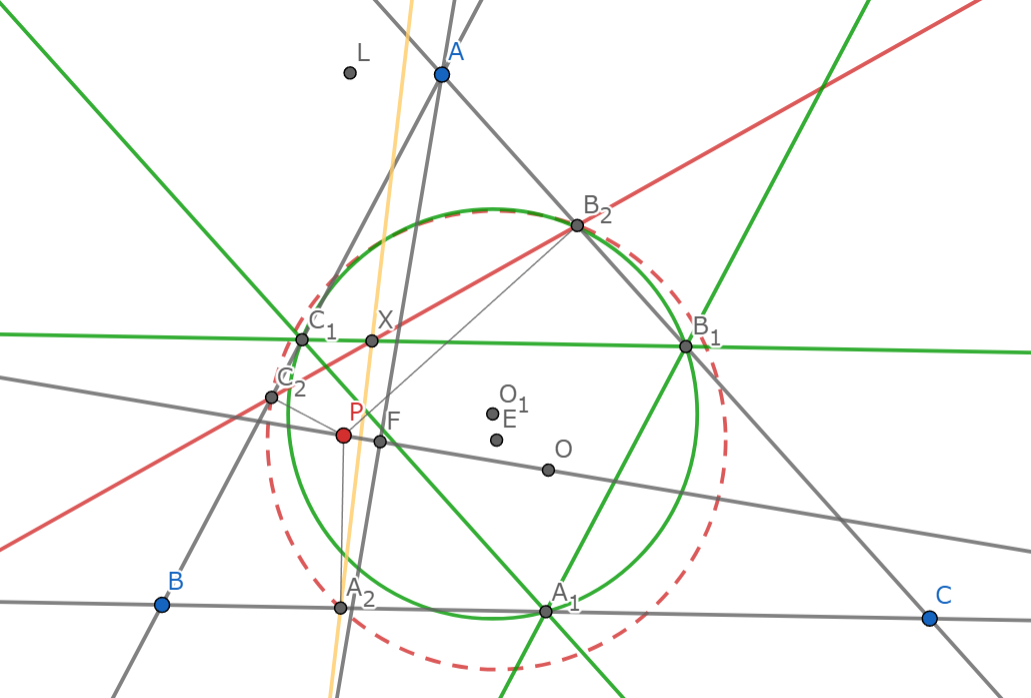
　いま明らかに$AL\parallel BC$であるから，$\angle ALP=90^\circ$である．

　$A,C_2,P,F,B_2$は$(AP)$上にあり，$A,C_1,F,O,B_1$は$(AO)$上にあるから，$\angle FC_1X=\angle FAB_1=\angle B_2C_2F=\angle XC_2F$ が得られ，$C_1,X,F,C_2$は共円．

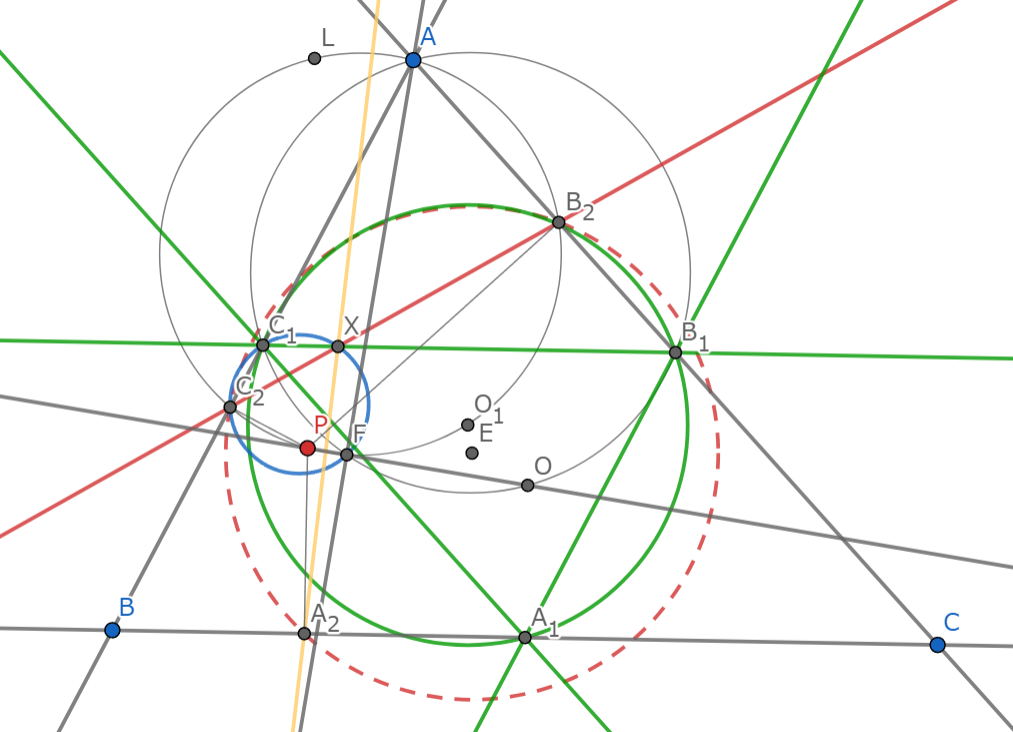
　直線$FX$と$(AP)$の交点を$L'$とするとReimの定理（aminoの補題）から$AL'\parallel B_1C_1$がわかるから$L=L'$，すなわち$L,X,F$は共線．

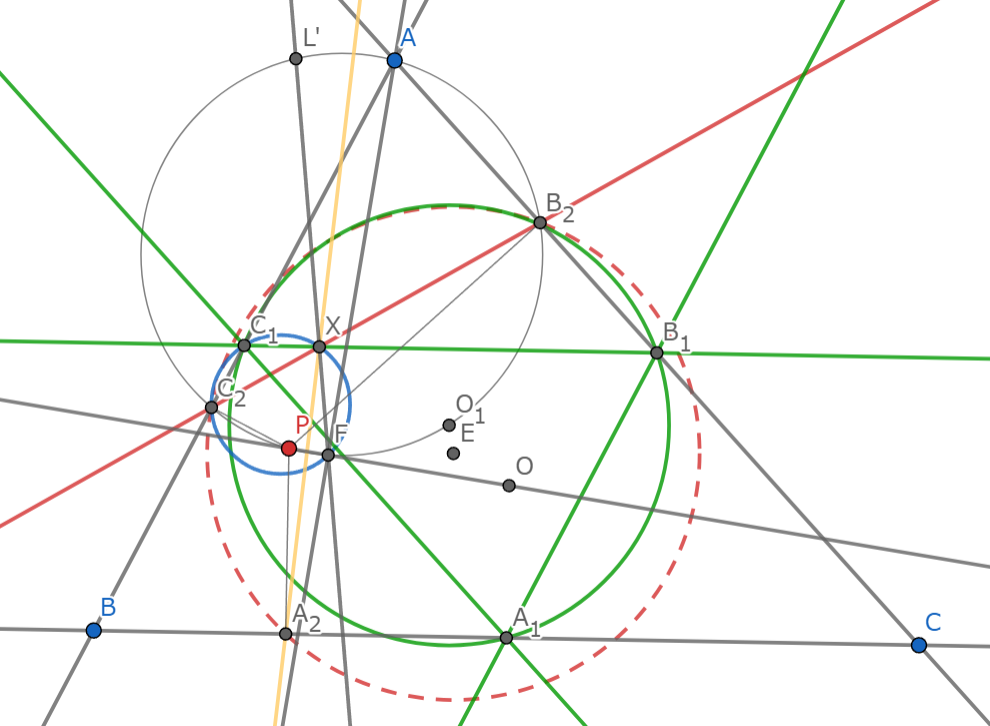
　直線$A_2X$と$(A_1B_1C_1)$の交点を$Q$し，$Q$を直線$B_1C_1$に関し対称移動した点を$F'$とする．直線$B_1C_1$に関する対称変換を$S_{B_1C_1}$とする．いま$S_{B_1C_1}$で$A$は$A$から$BC$に降ろした垂線の足にうつるが，これは$\triangle ABC$の九点円$(A_1B_1C_1)$上にある．したがって$F$は$(AO)$上にあるとわかる．

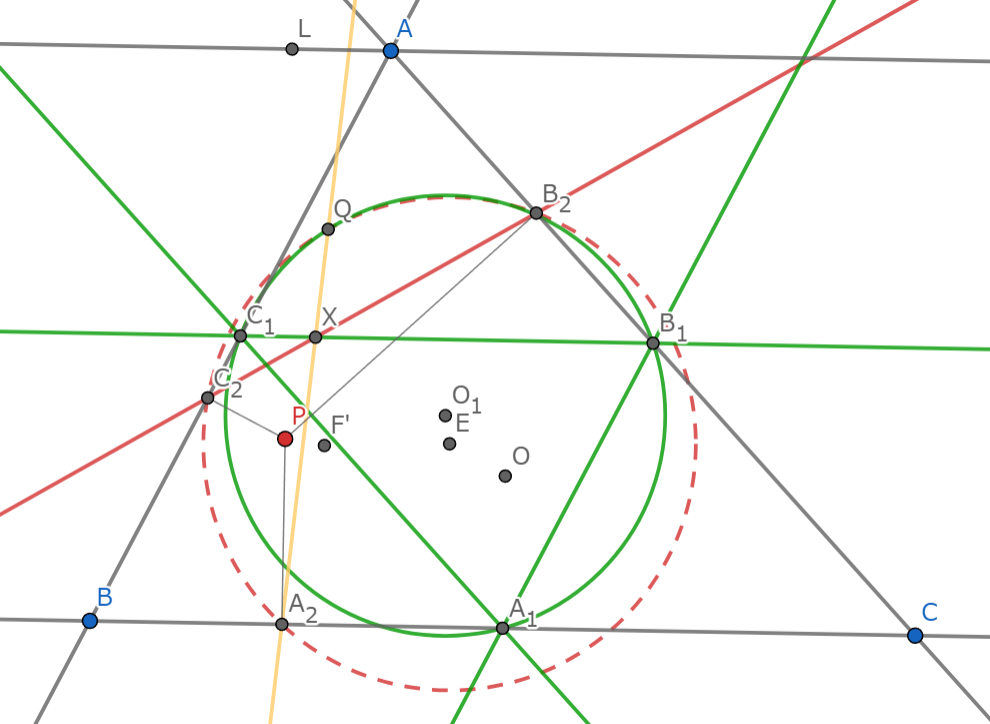
　さらに$S_{B_1C_1}$は$A_2$を$L$にうつす．これと$A_2,X,Q$の共線をあわせ$L,X,F'$の共線がわかる．以上より$F=F'$であるとわかる．したがって$XL\times XF=XQ\times XA_2=XB_2\times XC_2$であるから$Q$は$(A_2B_2C_2)$上にある．よって示された．

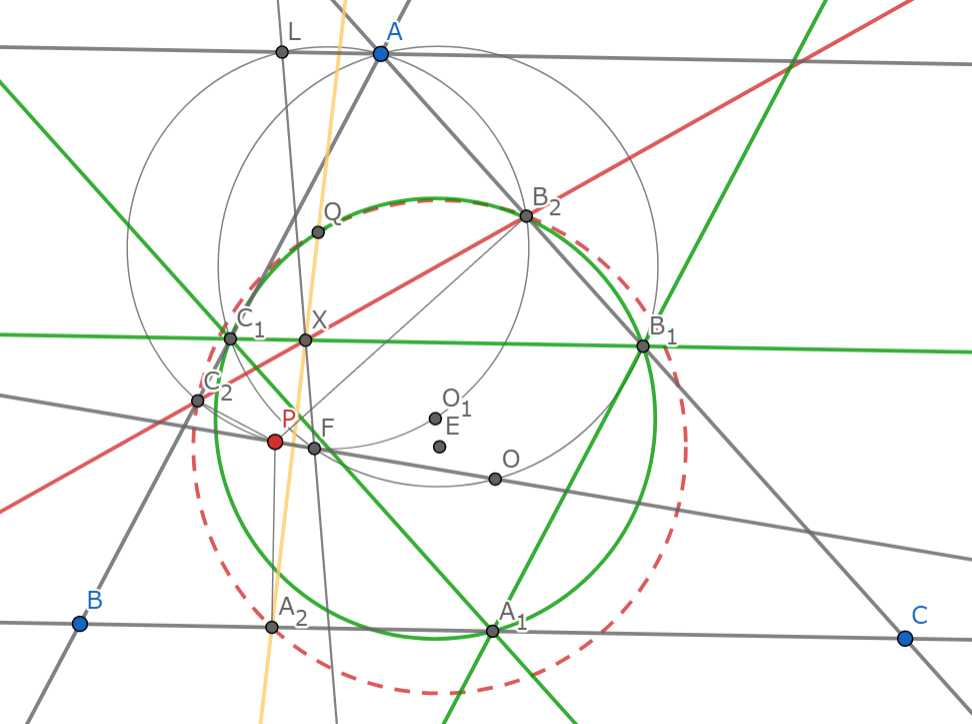
第二フォントネーの定理（直線の方）

Fontene's Second Theorem（直線の方）

　三角形$ABC$とその外心$O$を通る定直線$d$に対し，$d$上を点$P$が動くとき，$P$の垂足円は九点円上の定点を通る．

!FORMULA[69][37112][0]が青線上を動くとき!FORMULA[70][37143][0]が定点 $P$が青線上を動くとき$Q$が定点

　上の証明（$Q$と$F$が$B_1C_1$に関し対称）と，$O$が$\triangle A_1B_1C_1$の垂心であることをあわせて$Q$は$d$の九点円に対する反シュタイナー点である．特にこれは定点であるから示された．

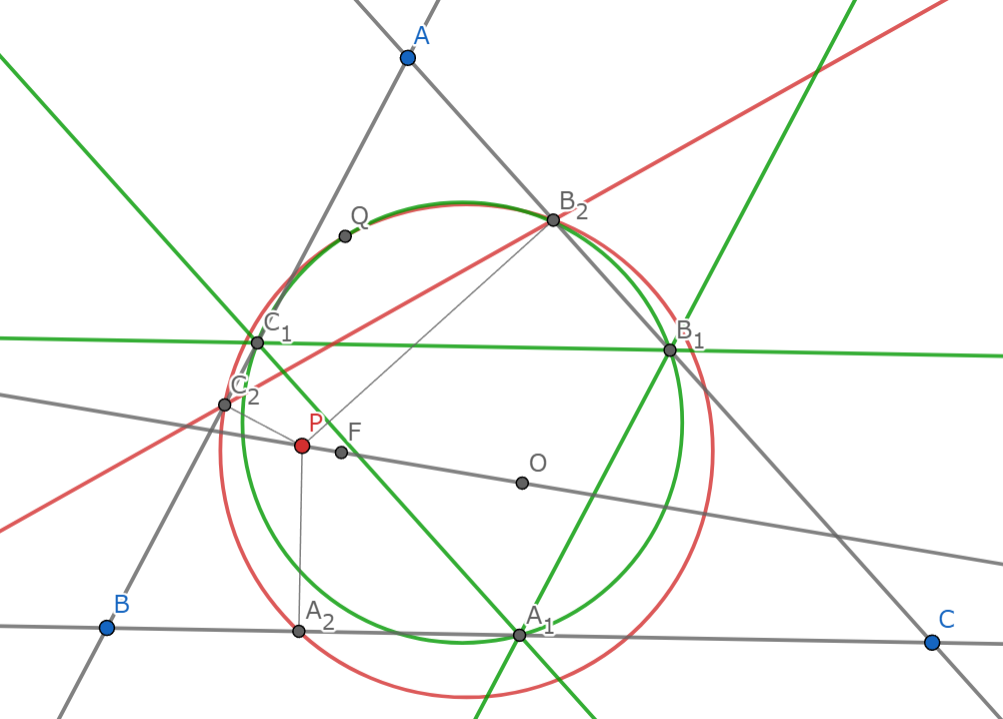
第二フォントネーの定理（強化版）

Fontene's Second Theorem（強化版）

　三角形$ABC$とその外心$O$を通る定直線$d$に対し，$\mathcal{H}$を$d$の三角形$ABC$での等角共役の像とすると，$d$または$\mathcal{H}$上を点$P$が動くとき，$P$の垂足円は$\mathcal{H}$の中心（特にこれは九点円上の定点）を通る．

$\mathcal{H}$上で動く点を$P'$とし，その等角共役点（$d$上を動く）を$P$とします．他の点の名前は定理2から引き継ぎます．

　$P$と$P'$は垂足円を共有するから，$\mathcal{H}$の中心が$Q$であることを示せば良い．todo：書く

第三フォントネーの定理

Fontene's Third Theorem

　三角形$ABC$と点$P$について，$P_0$を$P$の等角共役点とすると，$P$の垂足円が九点円と接することは$O,P,P_0$が共線であることと同値．

　$(A_1B_1C_1)$と$(A_2B_2C_2)$が再び交わる点を$Q'$とすると，$Q'$は$OP_0$の反シュタイナー点であることがわかる．いま$Q=Q'$であることは2直線$OP,OP_0$が一致することと同値であるから示された．

演習問題

　三角形$ABC$について，その中点三角形を$\triangle A_1B_1C_1$とし，（$H$の）垂足三角形を$\triangle DEF$とし，3点$X,Y,Z$を$X=EF\cup B_1C_1,Y=DF\cup A_1C_1,Z=DE\cup A_1B_1$と定める．
　このとき3直線$DX,EY,FZ$は九点円上の一点で交わる．また，3直線$A_1X,B_1Y,C_1Z$も九点円上の一点で交わる．

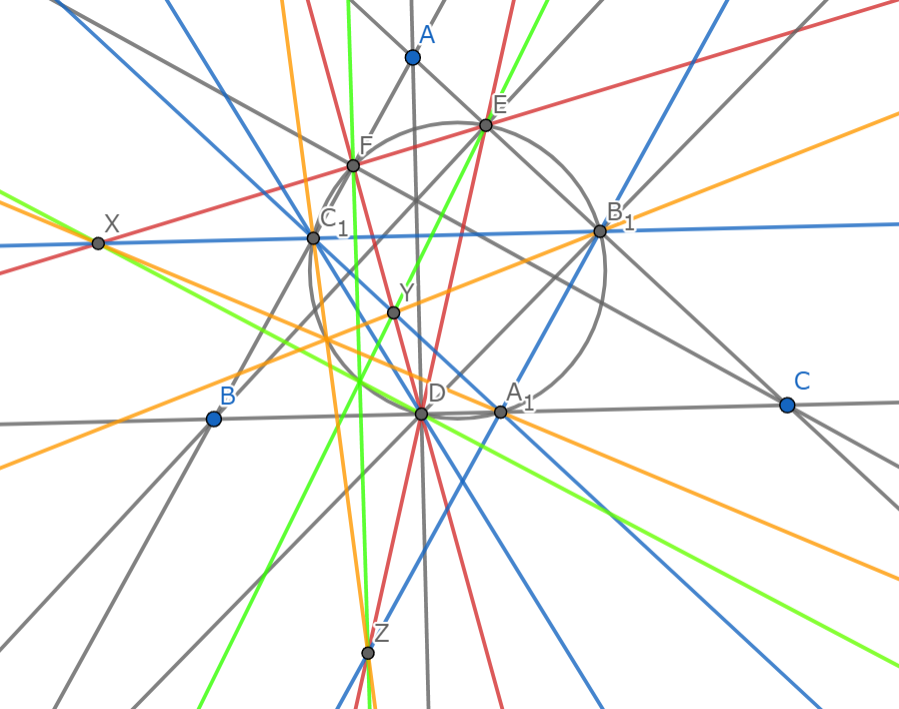
　Fontene's First Theorem より明らか．

(問題1の一般化)

　三角形$ABC$とオイラー線上の点$P$について，その中点三角形を$\triangle A_1B_1C_1$，$P$の垂足三角形を$\triangle DEF$とし，3点$X,Y,Z$を$X=EF\cup B_1C_1,Y=DF\cup A_1C_1,Z=DE\cup A_1B_1$と定める．
　このとき3直線$DX,EY,FZ$は九点円上の一点（特に問題1と同じ点）で交わる．

　オイラー線は外心を通るから，Fontene's First Theorem と Fontene's Second Theorem より明らか．

　三角形$ABC$について，その中点三角形を$\triangle A_1B_1C_1$とし，（$H$の）垂足三角形を$\triangle DEF$とし，3点$X,Y,Z$を$X=EF\cup B_1C_1,Y=DF\cup A_1C_1,Z=DE\cup A_1B_1$と定める．
　このとき，$(A_2B_2C_2)$の中心$O$は$\triangle XYZ$の垂心．