約数関数に関する予想
予想
次の不等式を満たす$2$以上の自然数$n$は$2,4,8,16$のみである.
$$\log_n(\sigma_1(n)) \geq \sigma_0(n)^{\frac{1}{2\Omega(n)}}$$
ここで,$\displaystyle{\sigma_x(n)=\sum_{d\vert n,0\lt d} d^x \ , \ \Omega(n)=\sum_{p^k\vert n\ ,\ p\in \mathbb{P}} 1 \ \ \ }$である.
つい先日ExcelのLAMBDA関数の存在を知りまして,『これでやっとちまちま計算して確認する苦労から解放される!』と意気込んで,数年ぶりにExcelを触りました.
Excelを用いて$n=10000$までは成立することを確かめています.
検証方法について
私が行ったExcelでの検証について紹介します.
関数$\sigma_x(n)$を
LAMBDA(a,b,SUM(POWER(UNIQUE(REDUCE(1,SEQUENCE(SQRT(a)),LAMBDA(c,d,IF(MOD(a,d),c,VSTACK(c,d,a/d))))),b)))(n,x)
で計算し,関数$\Omega(n)$を
LAMBDA(a,SUM(REDUCE(0,SEQUENCE(a),LAMBDA(c,d,IF(sigma(d,0)=2,VSTACK(c,IF(vp(a,d)>0,LAMBDA(a,d,MAX(REDUCE(0,SEQUENCE(LOG(a,d)),LAMBDA(e,f,IF(MOD(a,POWER(d,f)),e,VSTACK(e,f))))))(a,d),0)),c)))))(n)
で計算します.以降では簡略化のため,それぞれsigma(n,x) , omega(n) と書くことにして(『名前の定義』を使うとよいでしょう),予想の不等式を満たすx以下の自然数を配列として出力する計算式
=LAMBDA(n,UNIQUE(REDUCE(2,SEQUENCE(n-1)+1,LAMBDA(a,b,IF(LOG(sigma(b,1),b)-POWER(sigma(b,0),1/(2*omega(b)))>=0,VSTACK(a,b),a)))))(x)
のxにできるだけ大きな自然数を入れて結果を待ちましょう.
次の結果は x=10000 のときのものです.パソコンが悲鳴を上げ始めたのでここでやめてしまいました.
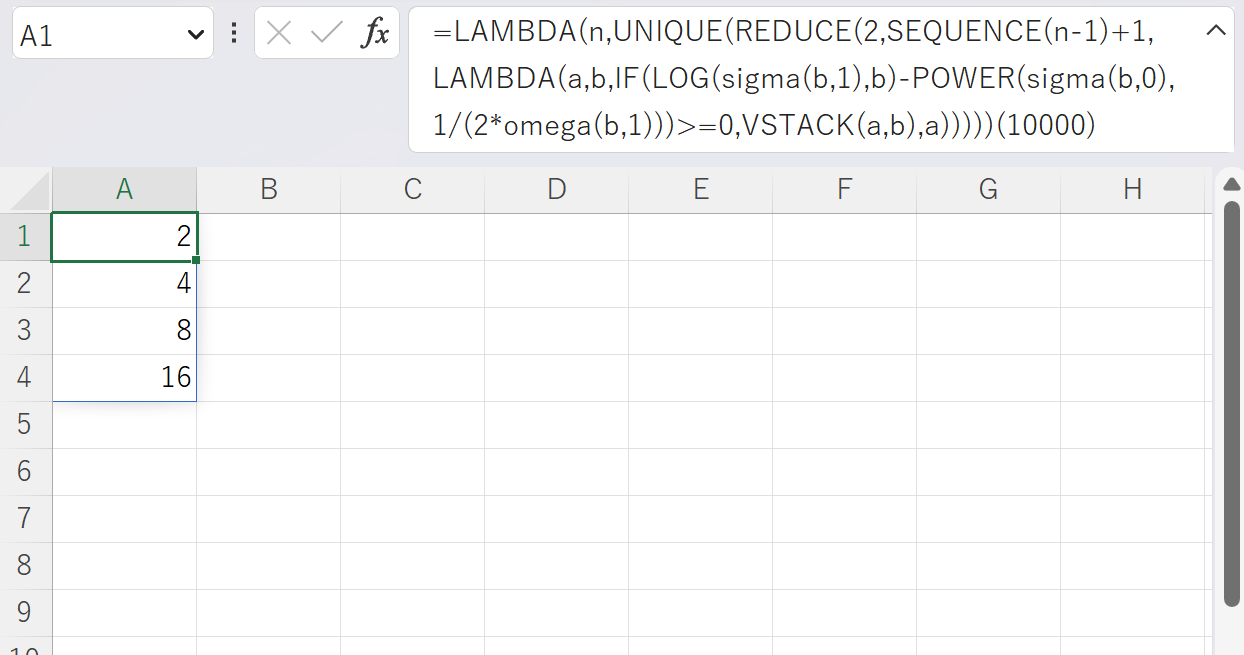 予想の検証(x=10000のとき)
予想の検証(x=10000のとき)
予想は正しそうだとわかります.予想と呼んでいるように,まだこの命題の真偽はわかっていません.とても悔しいことに今の私では証明できませんでした.ですので,この予想が証明(または反証)できたという方は私にご連絡ください.お待ちしております.
追記
式を改良し,$n=100000$までの自然数で予想が成立することを確認しました.
関数$\Omega(n)$を次のように改良しました.
=LAMBDA(x,IF(x>1,SUM(INDEX(REDUCE(VSTACK(0,0),SEQUENCE(x-1)+1,LAMBDA(a,b,IF(MOD(x,b),a,IF(REDUCE(0,SEQUENCE(SQRT(b)),LAMBDA(c,d,IF(MOD(b,d),c,c+1)))=1,HSTACK(a,VSTACK(REDUCE(0,SEQUENCE(LOG(x,b)),LAMBDA(e,f,IF(MOD(x,POWER(b,f)),e,e+1))),b)),a)))),1)),0))(n)
結局,素因数分解が速くなればいいので,素因数分解する式(図2)を改良して入れ込んだだけです.
これを『名前の定義』で「omega(n)」と書くことにします.
予想の不等式をみたすx以下の自然数を配列として出力する式を
=LAMBDA(n,UNIQUE(REDUCE(2,SEQUENCE(n-1)+1,LAMBDA(a,b,IF(LOG(SUM(UNIQUE(REDUCE(1,SEQUENCE(SQRT(b)),LAMBDA(c,d,IF(MOD(b,d),c,VSTACK(c,d,b/d)))))),b)-POWER(COUNT(UNIQUE(REDUCE(1,SEQUENCE(SQRT(b)),LAMBDA(c,d,IF(MOD(b,d),c,VSTACK(c,d,b/d)))))),1/(2*omega(b)))>=0,VSTACK(a,b),a)))))(x)
で計算します.xに100000を入れた結果,図3のようになりました.
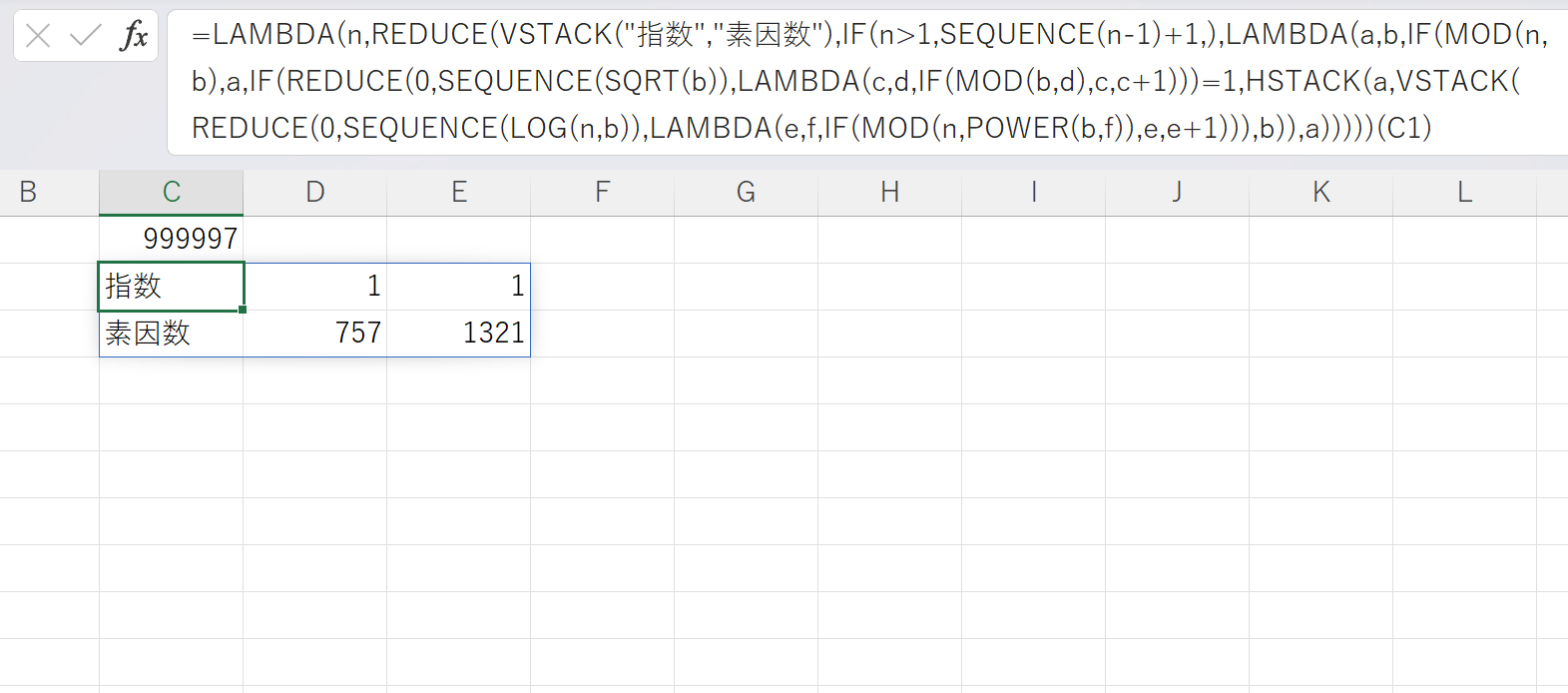 素因数分解の式(例:999997の場合)
素因数分解の式(例:999997の場合)
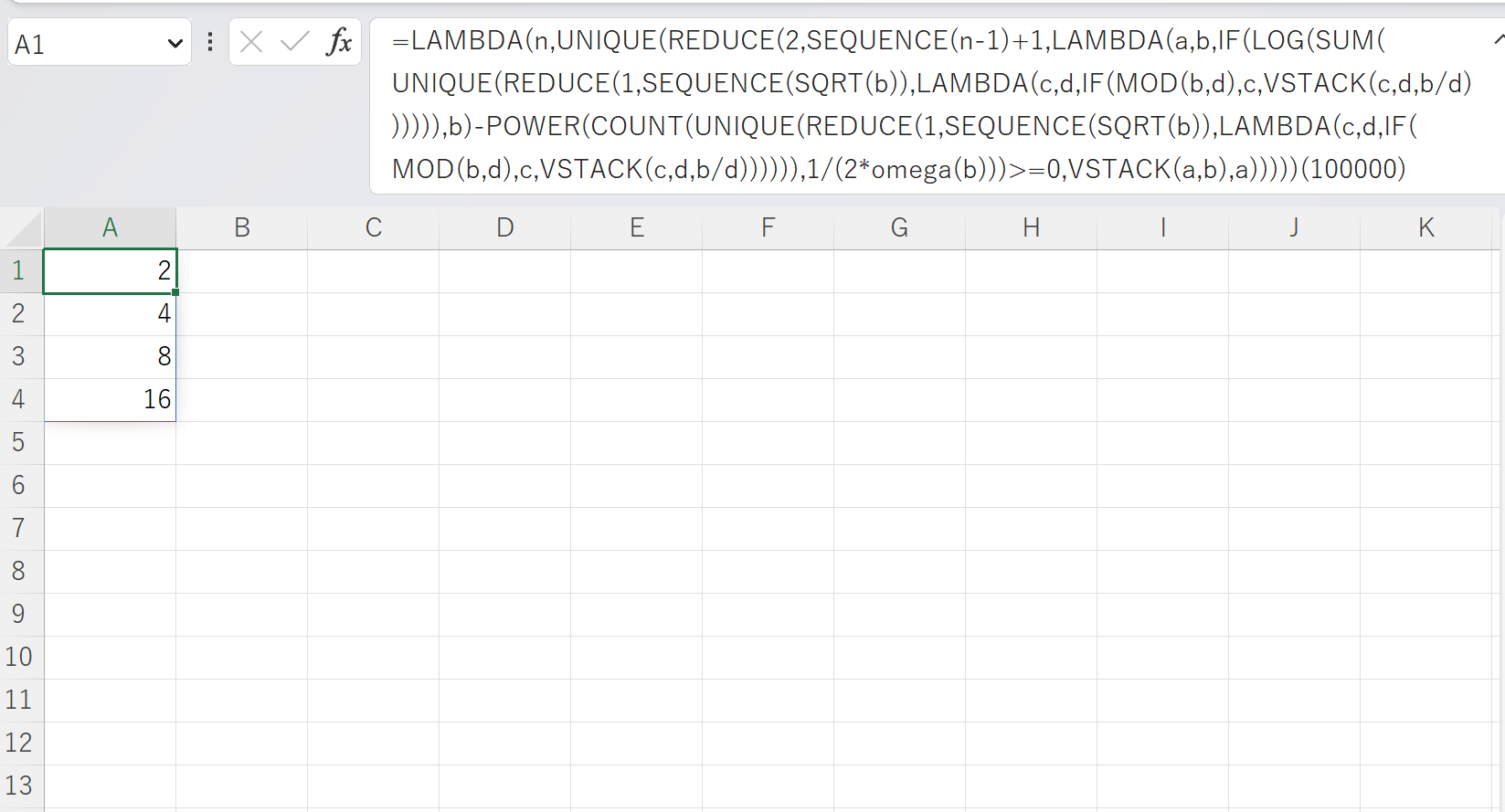 予想の検証(x=100000のとき)
予想の検証(x=100000のとき)
やはり予想は正しそうです.
