コラッツ予想の証明において、示した一般項の数列にすべての自然数が存在すればパスが一通りになるのか
コラッツの逆計算を表す、偶数・奇数の一般項を挙げ、その一般項が正しいかどうか、すなわちすべての自然数がこれらの数列に現れること・重複がないことを、数学的帰納法により証明することを考えました。
なぜ、それらの一般項ですべての自然数が表わせると、コラッツ予想の証明になるのかについて、考えを述べてみたいと思います。
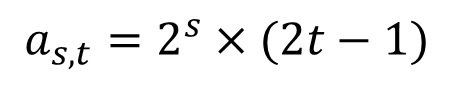偶数の一般項
偶数は、偶数の一般項において、もれも重複もなく表すことができ（数学的帰納法により証明可能）、その数列は奇数と奇数の間に存在するので、2で割り続けるとたどりつく奇数がどうならんでいるかについてを考えてみます。
その奇数の一般項は、2で割り続ける回数が偶数ならb_e,奇数ならb_oの式で示せます。
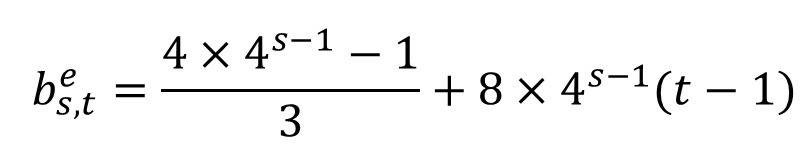奇数の一般項b_e
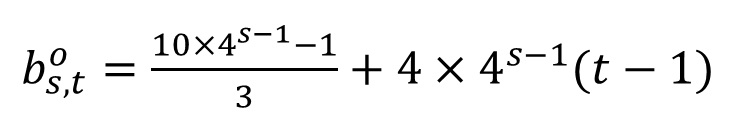奇数の一般項b_o
奇数の一般項において、tを定数としたときのb_eの数列、b_eの数列を考えます。
t=1のとき
b_e_t1(s)=1{1, 5, 21, 85, 341,…}
b_o_t1(s)=5{3, 13, 53, 213, 853,…}
t=2のとき
b_e_t2(s)=7{9, 37, 149, 597, 2389,…}
b_o_t2(s)=11{7, 29, 117, 469, 1877,…}
t=3のとき
b_e_t3(s)=13{17, 69, 277, 1109, 4437,…}
b_o_t3(s)=17{11, 45, 181, 725, 2901,…}
・
・
・
赤字の数は、連結する奇数で、その値は、
b_eのときは6t-5
b_oのときは6t-1
です。
これらの数列において、コラッツの計算をするとき、奇数だけに着目すると、{}の奇数から、赤字の奇数へ進みます。
b_e_t1(s)=1{1, 5, 21, 85, 341,…}
b_o_t1(s)=5{3, 13, 53, 213, 853,…}
の数列では、
1←1, 1←5, 1←21, 1←85, 1←341, …
5←3, 5←13, 5←53, 5←213, 5←853, …
のように参照できます。
s,tがすべての自然数をとるとき、{}にすべての正の奇数が現れるので、どんな自然数からコラッツ計算を始めても、つねに奇数←奇数の参照が存在し、それがずっと続きます。
同じ奇数は現れないわけですから、ループはありません。
いつも違う奇数が出現し、参照は繰り返されます。ただ一つ、1←1の参照のときのみ停止します。
なので、コラッツ計算を続けていくと、最後には1に到達します。
発散することもありません。
自然数の大きいところで発散するかもしれないと感じるかもしれませんが、ここで考える自然数全体では、すべて 奇数←奇数 の関係で数が並んでいます。
方向はいつも同じで、奇数（1つ）←奇数（多）で連結されていくのです。
連結されない系も存在しません。
すべての正の奇数が存在し、1←1のように同じ数を参照するのはこの1つのみだからです。
コラッツ計算のすべてが、この一般項の計算の数と数との関係に表われ、1方向に数をたどっていくことができます。計算が進むにつれて、計算結果に表われる可能性のある数は減っていきます。
例えば、b_o_t3(s)=17{11, 45, 181, 725, 2901,…}
では、17←45の参照をしたら、11, 181, 725, 2901,…の残りのb_o_t3(s)の数をもう通ることはありません。
どんどん通る可能性のある数は減っていき、1←1のように同じ数を参照するのはこの1つのみなので、1で終了することになります。
なので、コラッツの計算を施せば必ず1に到達すると言えると考えました。
