コラッツ予想を２進法で探求するための準備

はじめに

前の投稿、読んでくれた方々、ありがとうございます。
えどがわさんの投稿が新鮮な刺激になって、色々やってみたいことが増えてきました。
その前に、今までやってたことをちょっと整理してお伝えしたいと思います。

２進法モノクロ表示

個人的には『パンダ表示』という言葉を流行らせたいところです。
前の投稿でもお目にかけましたけど、直感的にわかりやすくていいです。

『２で割る』こと

何がいいかって、任意の自然数は２進法で表すことができますよね。んで、『２で割る』って操作は、１ビット右にずらす、『２をかける』って操作は、１ビット左にずらすことに相当します。例えば、
$28_{(10)}=11100_{(2)}$
$14_{(10)}=1110_{(2)}$
$7_{(10)}=111_{(2)}$
ここで、下付きの括弧の中の数字は、『何進法で表しているか』を表す数字です。
『２８』から始めて、２で２回割って『７』になる様子を、２進法モノクロ表示してみますね。
$28→14→7$

１個ずつ右にシフトしていく様子がわかりやすくて、よくないですか？

偶数は２進法で表すと必ず末尾が『０』になります。なので、『２で割る』という操作は、２進法では『末尾の０を取る』ことに相当します。コンピュータ科学を学ぶ方々には基本中の基本なんでしょうね。私も昔、アセンブラに関する初心者向けの本で読んで、『へー！』って思いました。考えてみれば、１０進法で表した自然数、１０の倍数なら末尾に『０』が付くし、『１０で割る』のは『末尾の０を取る』ってところ、一緒ですね。

『３倍して１を加える』という操作

すみません、無駄話が長くて。先を急ぎましょう。
『３倍して１を加える』という操作は、${ 3n+1=2n+n+1 }$なので、${ n }$を2進法で表したやつを１ビット左にずらしたビット列と、もとの${ n }$を２進法で表したビット列と足し算して、さらに最下位ビットを繰り上げることになりますね。（あー、言葉にすると、わかりにくいなー、ごめんなさい。）
具体的に見ていきましょう。
例えば、$n=9$として、${3 \times 9 +1 }$を、順番にやってみます。
まず、${3 \times 9 =9+9 \times 2=27}$、これを２進法のモノクロ表示（『パンダ表示』と呼びたい）しますよ。
9+9×2=27
１行目が $ \ 9_{(10)}=01001_{(2)}$
２行目が$18_{(10)}=10010_{(2)}$
３行目が$27_{(10)}=11011_{(2)}$
になってるのがわかるかな？
みんなー、このくらいは大丈夫だよね。
じゃぁ、ここに１を足しまーす。
27+1=28
１行目が$27_{(10)}=11011_{(2)}$
２行目が $1_{(10)}=00001_{(2)}$
３行目が$28_{(10)}=11100_{(2)}$
２回繰り上がって下２桁が０になってますね。

初期値９→２８→１４→７→…→１

普通のコラッツの手順で、初期値９で１になるまでをモノクロ(パンダ)表示してみます。
通常のコラッツ変換で初期値９から１になるまで
やっぱり２で割るの、まどろっこしいですよね。
ぜーんぶ右に詰めちゃえばいいじゃん、ってのが次のやつ。

『２で割れるだけ割ってみました』的な何か

初期値９から偶数を省略して、
９→７→１１→１７→１３→５→３→１
って数列をパンダさんにしてみると、
コラッツ変換偶数省略バージョン初期値９
んー、これはこれでスッキリはしてるんだけど、なんか大事なことが抜けてるような感じがするんですよね。それで考えたのが、『奇数に対応するビット列に対して、１ビット左にシフトしたやつを元のビット列に足して、最下位ビットを繰り上げる』って操作（要するに”3n+1”だね）を繰り返してったのが次のやつ。

『２進３倍繰上げルール』

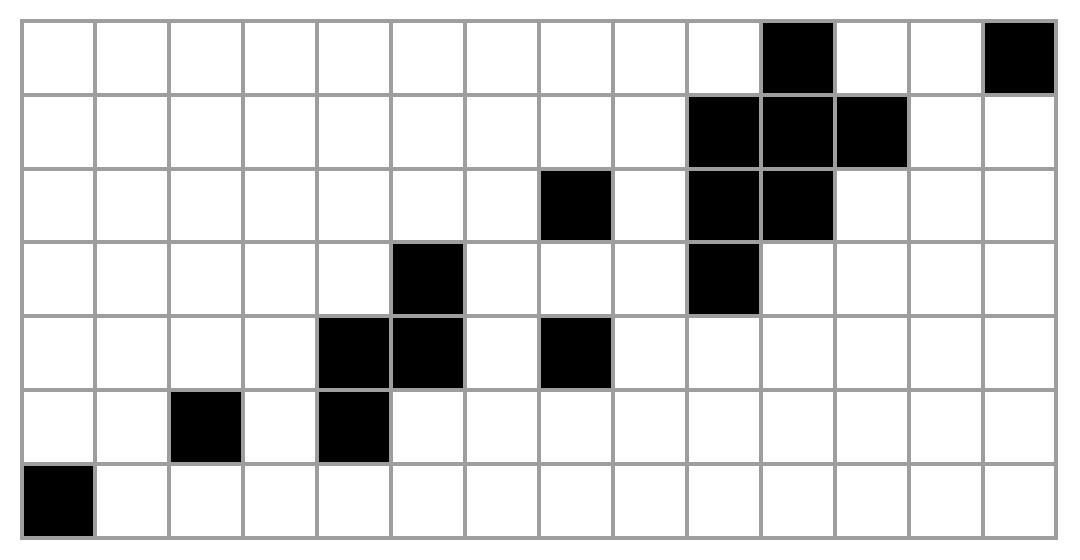『２進３倍繰上げルール』の初期値９で１になるまで
この表し方の何がいいかって、１回の”3n+1”の操作のあと、２で割らなきゃいけない回数が、最下位ビットのズレとして一目でわかることですかね。
さらにそのおかげで、図全体の長方形の縦と横の長さについて、次のことが言えます。
(縦の長さ)-1：初期値の奇数から最終値『１』になるまでの間に、何回”3n+1”の操作を施したか
(横の長さ)-1：同じく初期値の奇数から最終値『１』になるまでの間に、トータルで何回２で割ったか
ごめんなさい、ここで安易に『最終値』なんて言葉は使うべきでないかもしれないですよね。あくまでまだ『１にならないで繰り返す反例』が見つかってないだけですもんね。

結び

ここまで読んでくださったみなさん、ありがとうございました。
なんだかんだで前の投稿と大した違いはなかったですね。
お詫びに、これからいくつか画像を載っけます。
それらから読み取れること、コメント欄でお知らせいただけるとありがたいです。
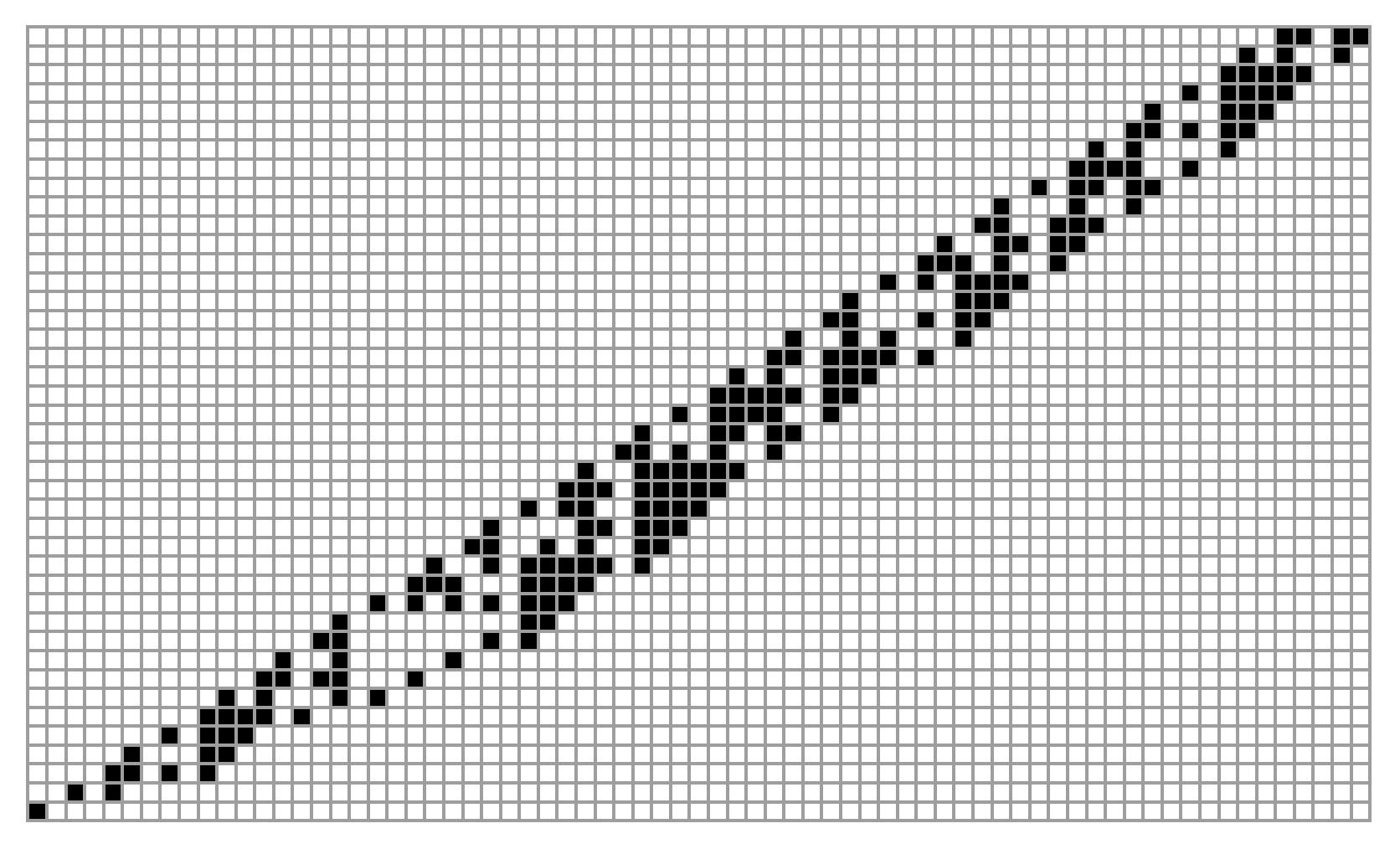悪名高き初期値２７
ビット列が一番長いのどーこだ？
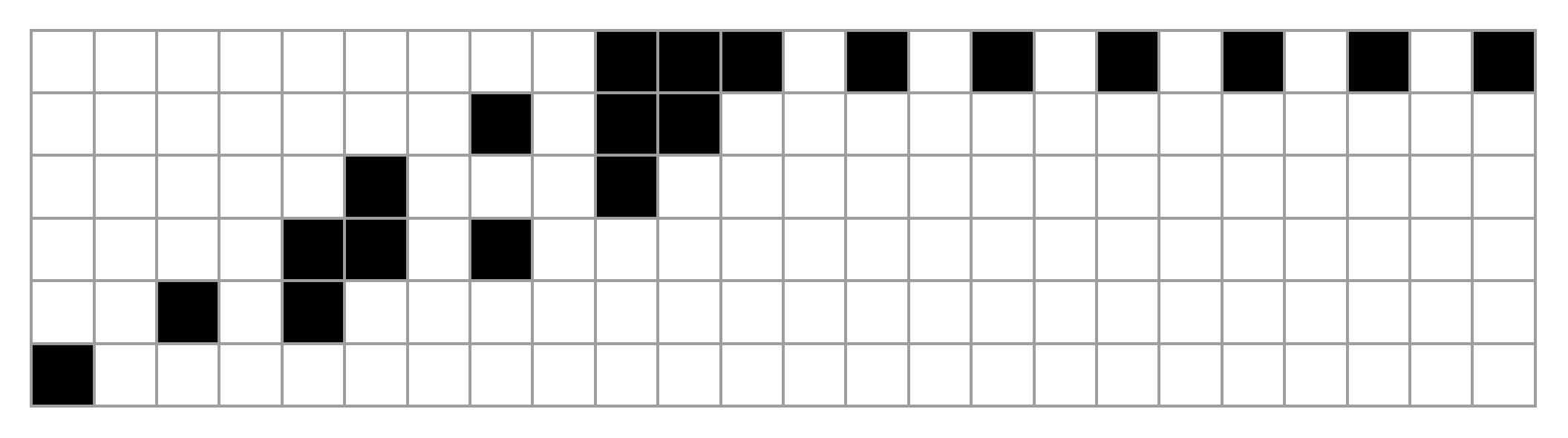『第１しましましっぽの定理』
初期値３００３７って初期値７といっしょやん！
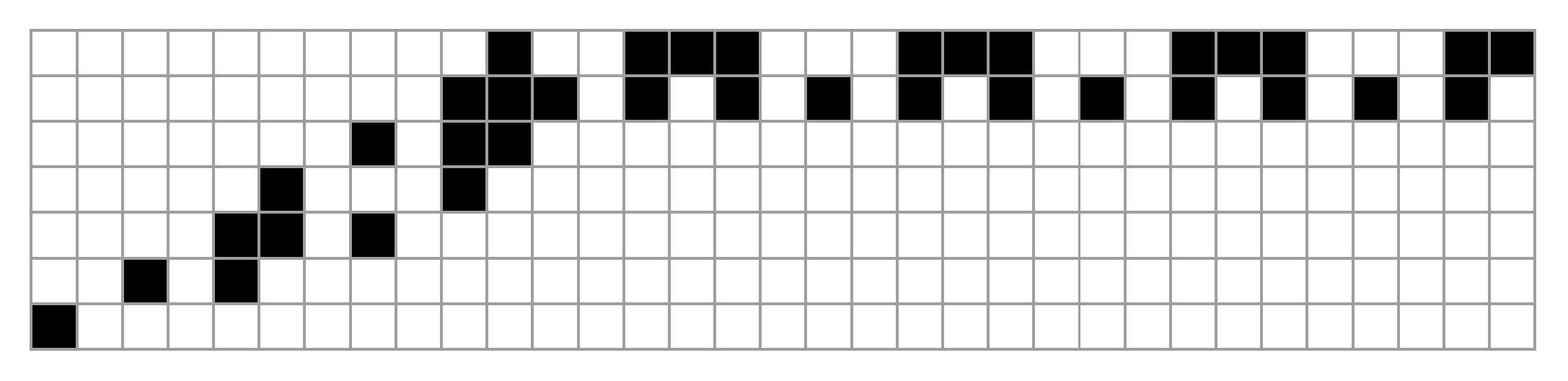『第２しましましっぽの定理』
初期値5126371ってまたすぐ初期値７と一緒になるやん！
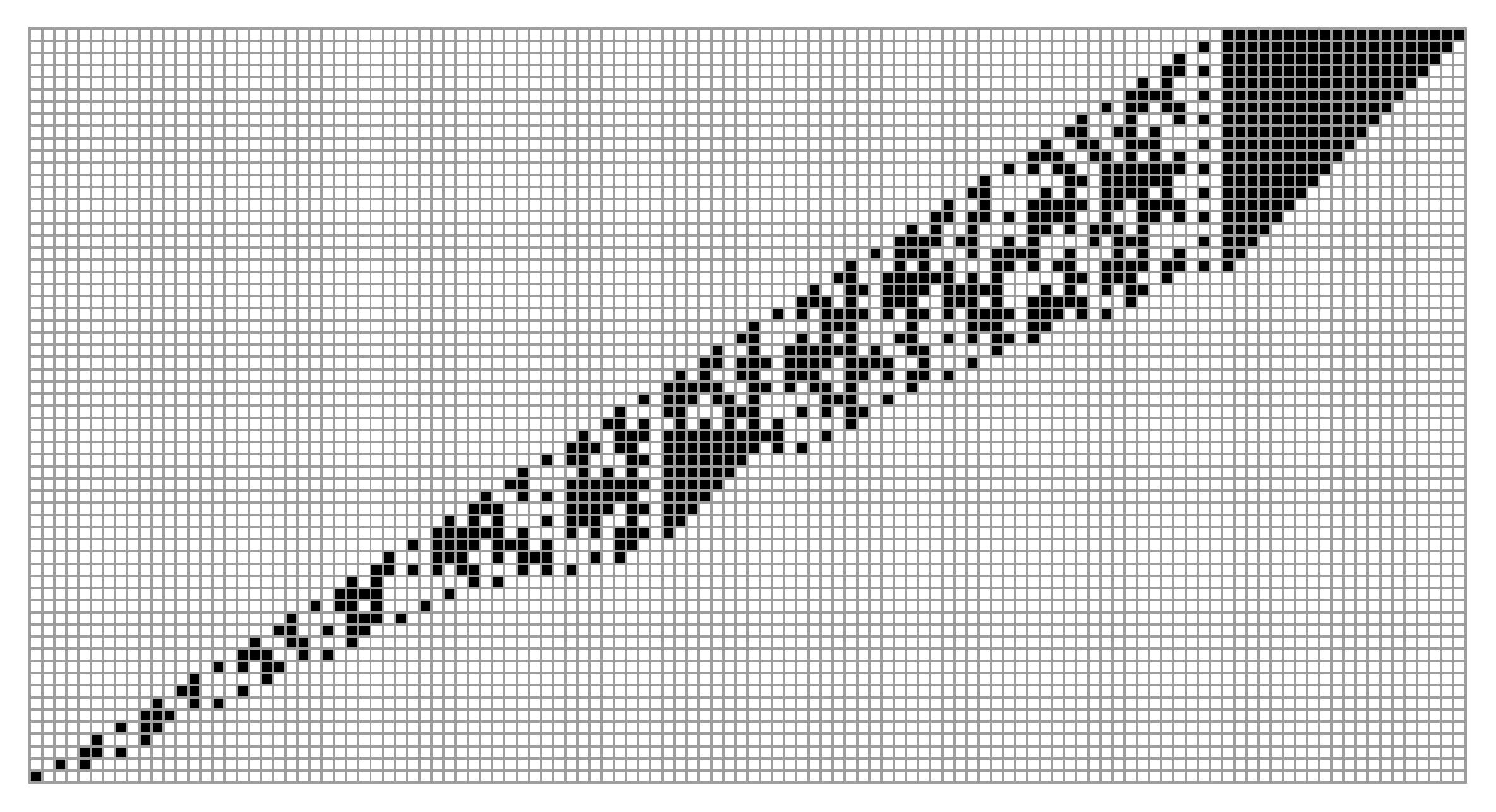『黒三角の定理』初期値2^20-1
ビット列が長くなるときってどういうときかわかりますねん
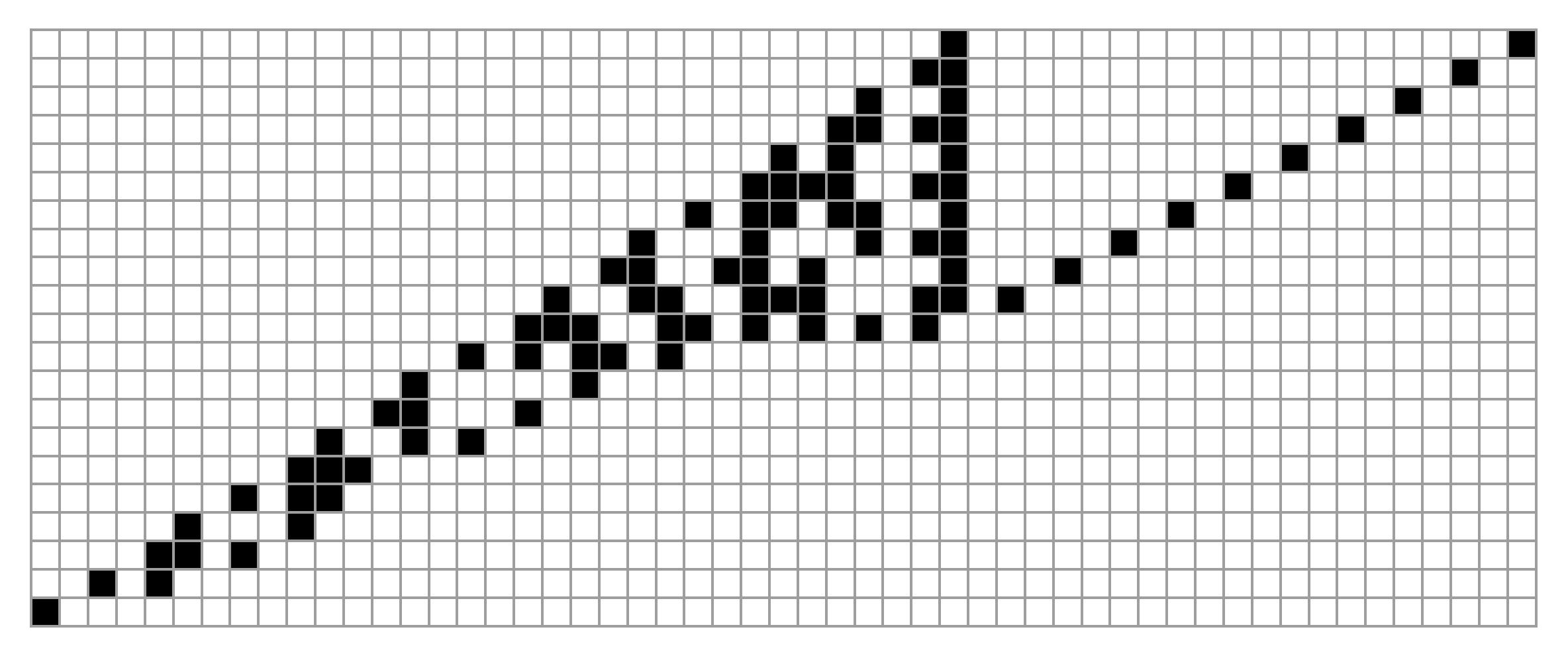『白三角の定理』初期値2^20+1
上位ビットは”３の累乗”やん！
以上、ご覧いただき、ありがとうございました。
コメント、お待ちしてます。
m(_ _)m