コラッツ予想と２進法：有限長ビット列の有理数化によるアプローチ

はじめに

　ご無沙汰してました。
　コラッツ予想を２進法で考え２０年ほど経過しました。
　２年ほど前に見つけたことを紹介します。
　興味を持っていただけると嬉しいです。

発想のきっかけ

　以前の記事で、コラッツの手順で出てくる奇数列を２進法で表すと、『３倍して、最下位のビットを繰り上げる』のと一緒、みたいな話を書きました。
　２年ほど前に『奇数と有限長ビット列が１対１対応するのはいいんだけど、奇数って、ほっとくと変にでかい数になったりするの、やだなー』と思い始めました。
　そこで考えたのが、『有限長ビット列を１以上２未満の有理数に１対１対応できねーかな』って発想でした。
　「なんで『０以上１未満』じゃねーの？」って？
　実は、以下の変換により、『最上位ビットを$2^0$の位にした方が良くね？』と思ったからです。

有限長ビット列の有理数化

　ここからちょっと数式で表します。
　ある奇数 $n_{odd}$ が長さ $l$ ビットの２進数で表されたとしますね。
　つまり、
　$n_{odd}$ $ = $ $\sum_{k=0}^{l-1}$ $a_{l-k}$ $2^{l-(k+1)}$
　ここで、$a$ の添字や$2$ の指数が変な感じがしますが、最上位ビットを $a_l$, 最下位ビットを $a_1$ として、最上位ビットから順に足していることにしてます。
　この $\lbrace a_l, a_{l-1}, \cdots ,a_1 \rbrace$ を、こんなふうに有理数 $r$ に直すことにします。
　$r$ $=$ $\sum_{k=0}^{l-1}$ $a_{l-k}$ $2^{-k}$
　（あらためて数式に表してみるとすっきりするー。）
　具体的な奇数でやってみますね。
　例えば、１０進法の『１９』って、２進法で表すと『１００１１』になりますよね。
　つまり、
　$19_{(10)}$ $=$ $10011_{(2)}$

　ここで出てきた $\lbrace 1,0,0,1,1 \rbrace$ を、
　$1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 $ $=$ $19_{(10)}$
　から、
　$1 \times 2^0 + 0 \times 2^{-1} + 0 \times 2^{-2} + 1 \times 2^{-3} + 1 \times 2^{-4} $ $=$ $1.1875_{(10)}$
　に変換する、ってことね。
　これだと任意の奇数を１以上２未満の有理数に１対１対応で変換できますよね。

『コラッツの奇数列の有理数化』の具体例

　例えば、初期値$9$ から始めて、コラッツの手順で変化させていくと、
　$\lbrace 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 \rbrace$
　ですよね。
　これを、奇数だけ引っ張り出すと、
　$\lbrace 9, 7, 11, 17, 13, 5, 1 \rbrace$
　ってなりますね。
　これをいつもの『２進３倍繰上げ』の『白黒表示』にするとこうなります。
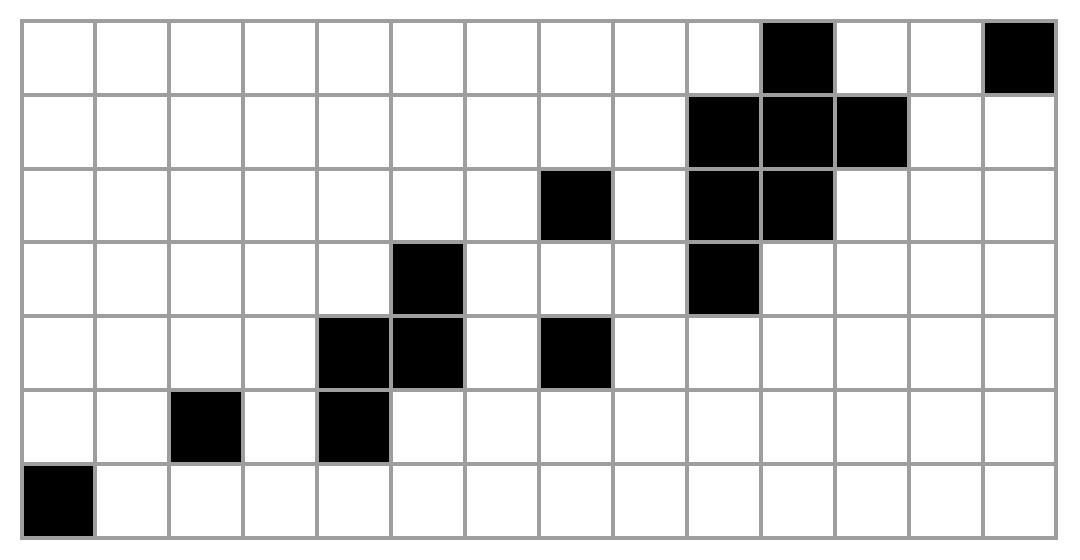『２進３倍繰上げルール』の初期値９で１になるまで
　この図は前に書いた記事からの流用です。
　これを、さっきの方法で有理数化してグラフにしたのがこちらです。
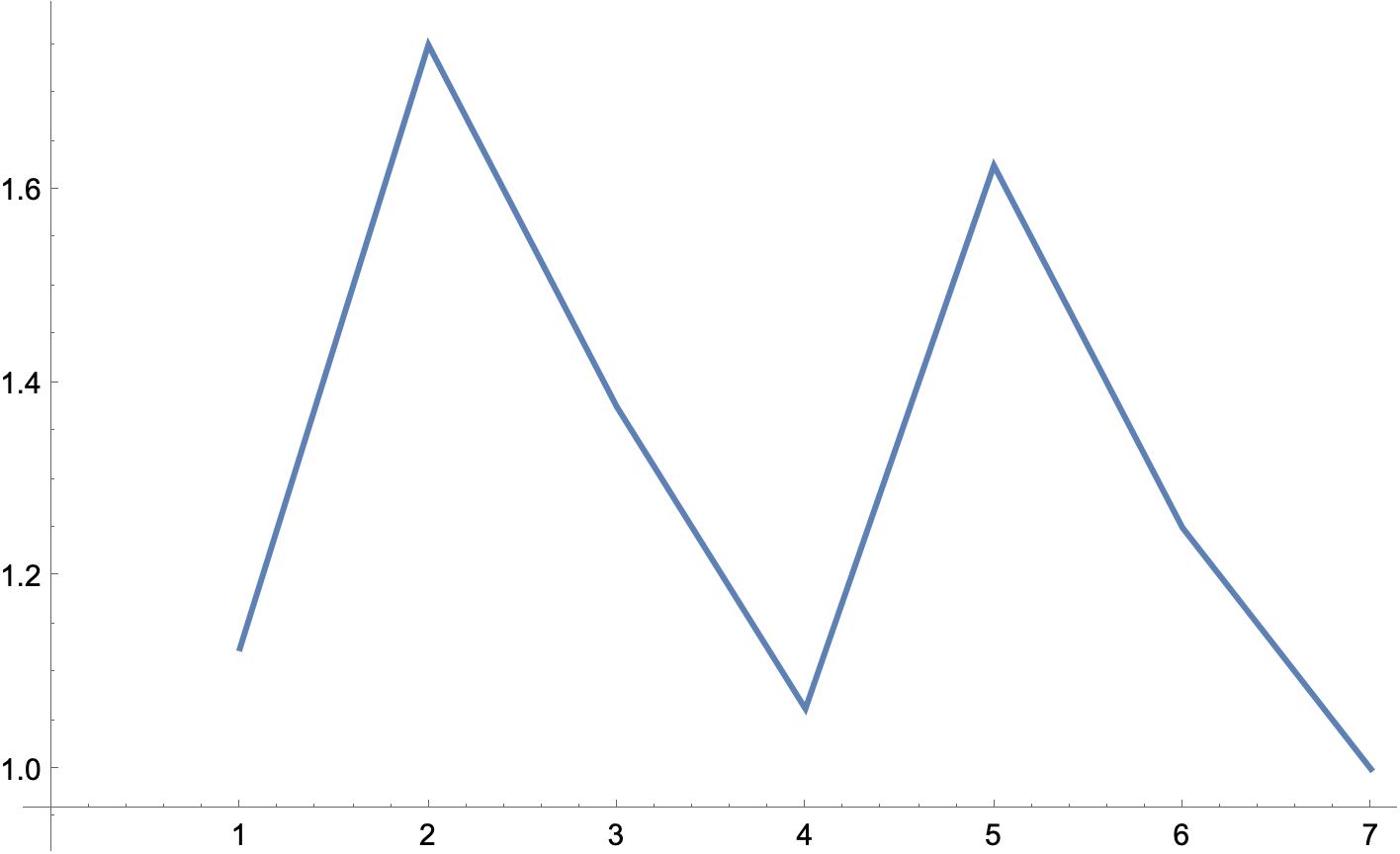初期値９でコラッツの奇数列を有理数化したグラフ
　これだけ見ても、『初期値９を有理数1.125に変換して、最後1.00になっとるだけやないけ』と言われそうですが、その通りです。
　びっくりしていただくのはここからです。

悪名高き『初期値２７』

　すでに何度か見ていただいているかと思いますが、初期値２７にすると、
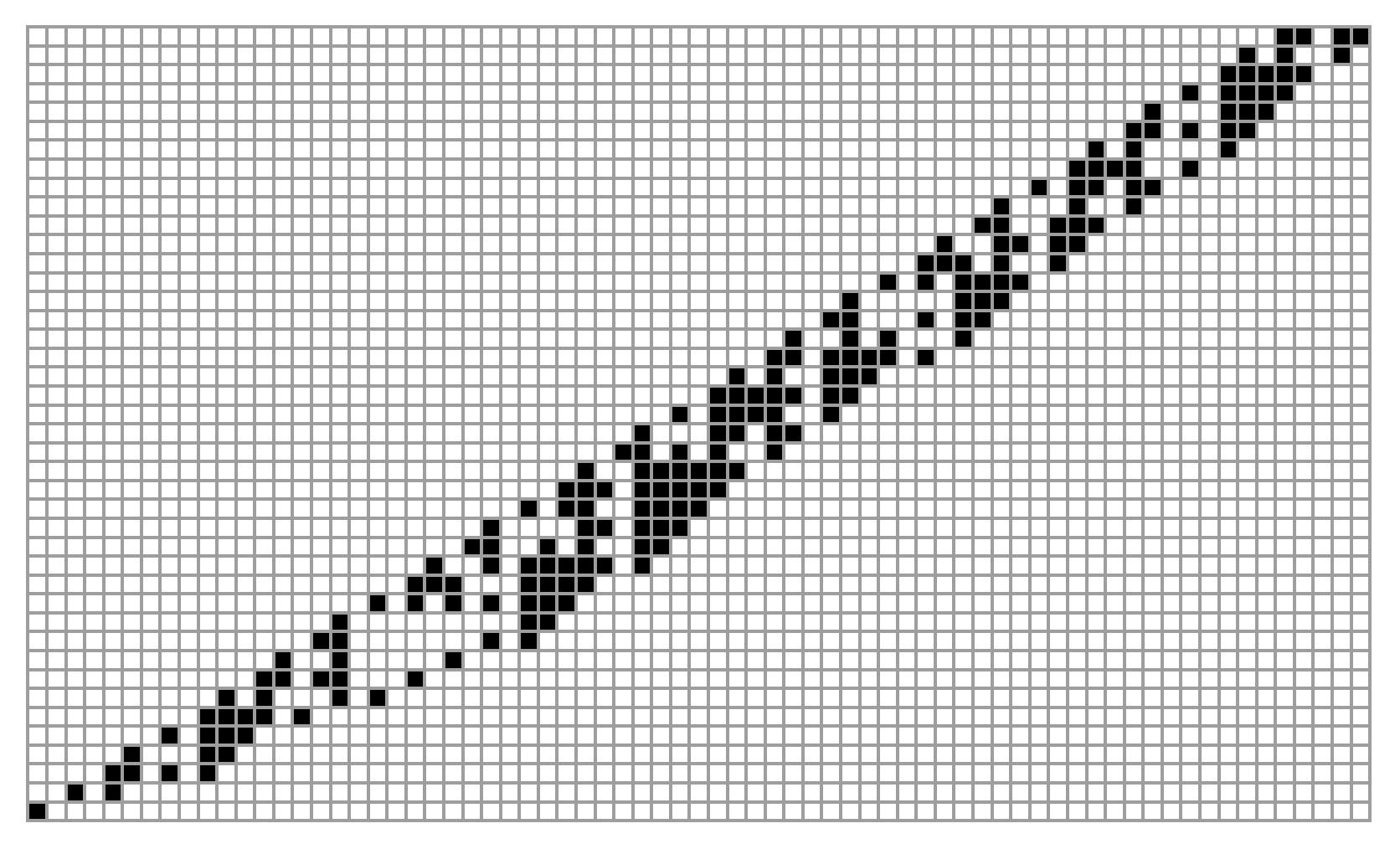悪名高き『初期値２７』
　これを有理数化してグラフにすると、こうなります。
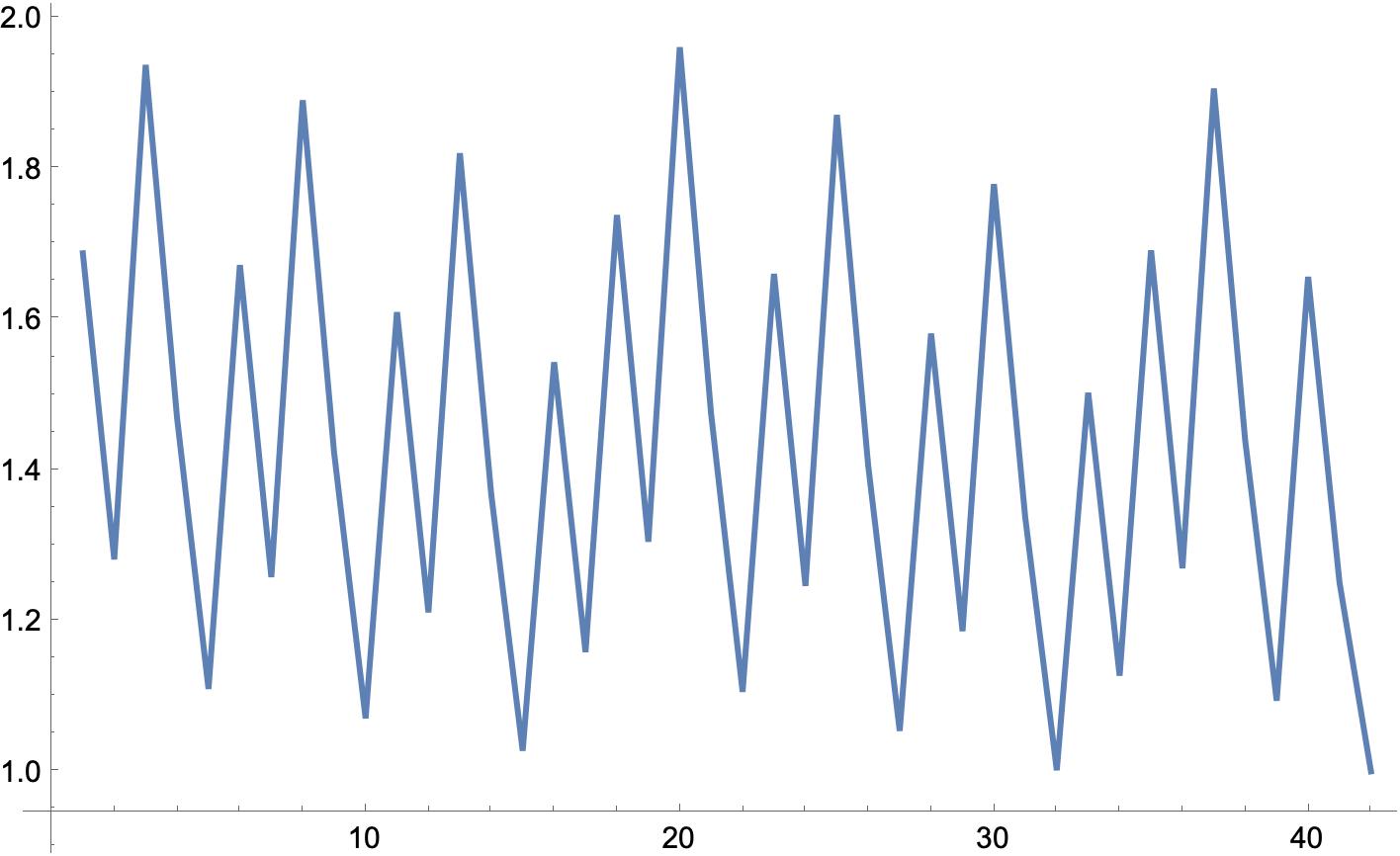『初期値２７』で奇数列を有理数化
　んー、まだまだ、『増えたり減ったりしてるだけ』にしか見えませんよね。
　ここで、線を消して、点だけにしてみます。
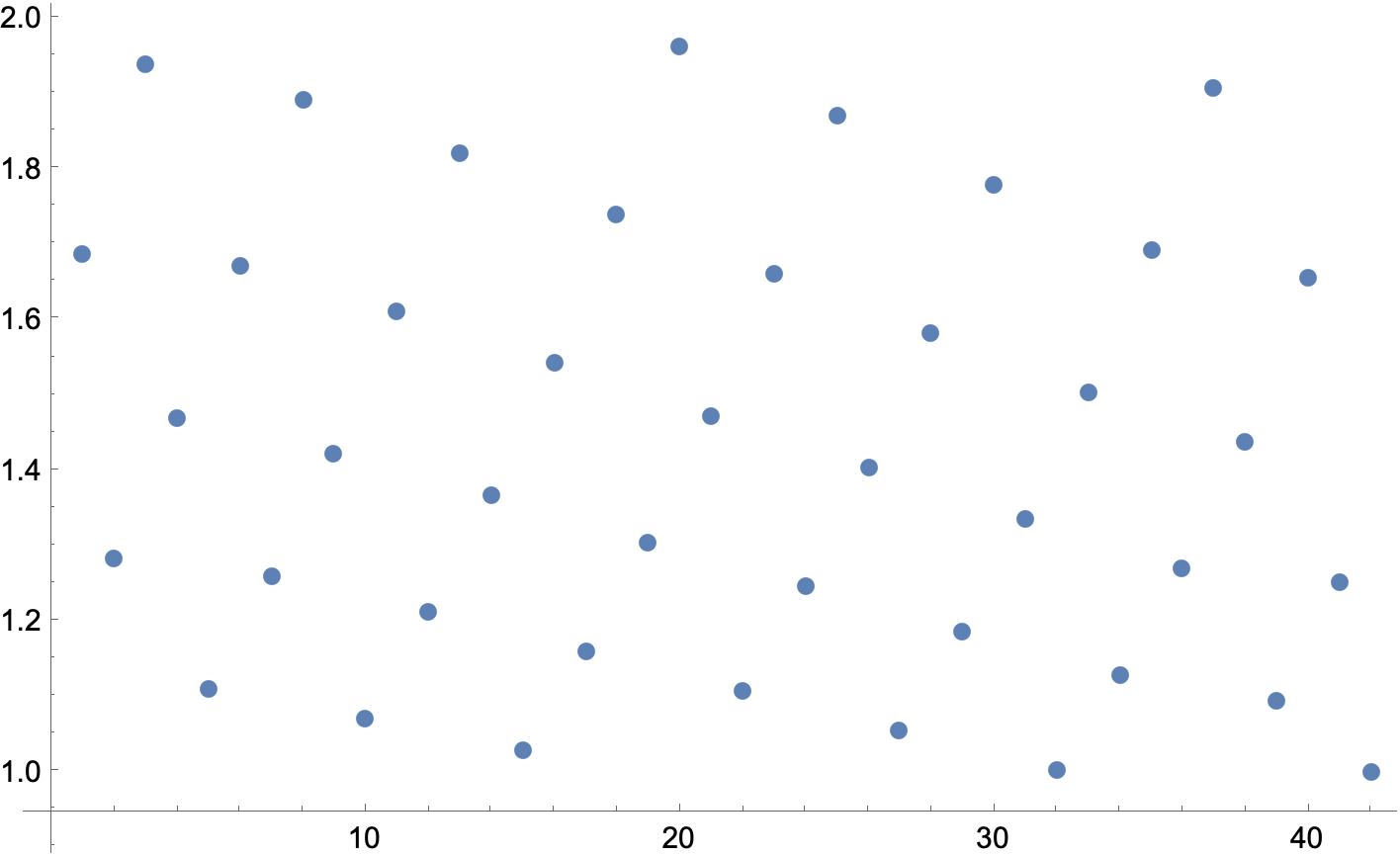『初期値２７』で奇数列を有理数化（線を消しました）
　いかがでしょう？
　点が綺麗に並んでる感じ、しますね。

初期値$2^{20}-1$

『初期値$2^{20}-1$』の『２進３倍繰上げルール』で白黒表示
　これをまた、有理数化して、点だけ打ってみます。
『初期値$2^{20}-1$』で得られる奇数列の有理数化

　点列が綺麗に曲線を描いていますね。
　最後の５or６個は曲線からずれている感じがします。
　これは、『最下位ビットからの繰上げの影響』だと思います。
　単純に、『３の累乗』を２進数表示して、さっきの方法で有理数化して点を打っていくと、綺麗な曲線が延々と続きます。

まとめ

　まとめというほどのお話にもなりませんが、２年ほど前にこの結果を得て、『コラッツ予想って結局のところ、奇数を３の累乗倍することと、最下位ビットを繰上げることの組み合わせなんだな』って、あらためて考えるようになりました。
　ここまで読んでいただいてありがとうございました。
　ご笑覧いただけてれば幸いです。(^_^)