オリジナル問題集No.1
あいさつ
んちゃ!
今回は色々な問題を作って遊ぶのだ!
問題のレベルを独断で分類しておくのだ。
⭐️・・・簡単
⭐️⭐️・・・普通
⭐️⭐️⭐️・・・難しい
【説明】
- 簡単専門的知識を要求しない問題なのだ
- 普通高校で習う程度の予備知識を要求する問題なのだ。
- 難しい専門的知識を要求しなおかつ、考察が必要な問題なのだ。
問題1 ⭐️
$|x|\lt 1$ならば、次の等式が成り立つ事を示せ。
\begin{equation}
\sum_{n=0}^{\infty}x^{n}=1+\sum_{n=1}^{\infty}x^{\frac{n(n+1)}{2}}\frac{1-x^{n+1}}{1-x}
\end{equation}
次の様に数を並べてみると良い。
各行について等比級数の公式を適用する事で直ちに本問題の等式が証明される。
| 0 | ||||
| 1 | 2 | |||
| 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | |
| 10 | 11 | 12 | 13 | 14 |
問題2⭐️
$x\neq 1$なる複素数に対して、以下の式が成り立つ事を示せ。
\begin{equation}
\sum_{m,n=1}^{N}x^{|m-n|}=N+2\frac{x^{N+1}-x^{2}}{(x-1)^{2}}-2(N-1)\frac{x}{x-1}
\end{equation}
| ■ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 |
| 3 | 2 | 1 | 0 | 1 | 2 |
| 4 | 3 | 2 | 1 | 0 | 1 |
| 5 | 4 | 3 | 2 | 1 | 0 |
\begin{eqnarray} \sum_{m,n=0}^{N}x^{|m-n|}&=&N+2\sum_{k=1}^{N-1}(N-k)x^{k}\\ &=&N+2\sum_{k=1}^{N-1}kx^{N-k}\\ &=&N+2x^{N}\sum_{k=1}^{N-1}kx^{-k}\\ &=&N+2x^{N}\frac{1}{1-x^{-1}}(\sum_{k=1}^{N-1}x^{-k}-(N-1)x^{-N})\\ &=&N+2x^{N}\frac{x^{-1}-x^{-N}}{(1-x^{-1})^{2}}-2(N-1)\frac{1}{1-x^{-1}}\\ &=&N+2\frac{x^{N+1}-x^{2}}{(x-1)^{2}}-2(N-1)\frac{x}{x-1} \end{eqnarray}
問題3⭐️⭐️
以下の式を証明せよ。
\begin{equation}
\int_{0}^{a}dx_{1}\int_{0}^{b}dx_{2}f(x_{1})f(x_{2})dx=\int_{0}^{a}dx_{1}\int_{0}^{\frac{b}{a}x_{1}}dx_{2}f(x_{1})f(x_{2})+\int_{0}^{b}dx_{2}\int_{0}^{\frac{a}{b}x_{2}}dx_{1}f(x_{1})f(x_{2})
\end{equation}
下の様に積分領域を分割する。
すると与えられた積分は下記の様に書ける。
\begin{equation}
\int_{0}^{a}dx_{1}\int_{0}^{b}dx_{2}f(x_{1})f(x_{2})dx=\int_{0}^{a}dx_{1}\int_{0}^{\frac{b}{a}x_{1}}dx_{2}f(x_{1})f(x_{2})+\int_{0}^{b}dx_{2}\int_{0}^{\frac{a}{b}x_{2}}dx_{1}f(x_{1})f(x_{2})
\end{equation}
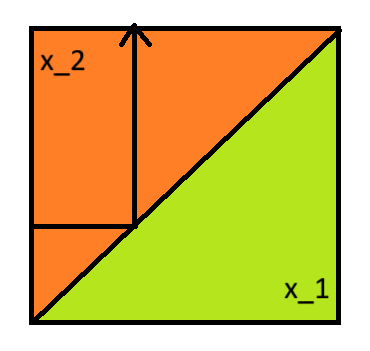 積分領域
積分領域
上記で特に$a=b$とすると以下の式が成り立つ。
\begin{equation} \{\int_{0}^{a}dxf(x)\}^{2}=2\int_{0}^{a}dx_{1}f(x_{1})\int_{0}^{x_{1}}dx_{2}f(x_{2}) \end{equation}
問題4⭐️⭐️
\begin{equation}
\int_{0}^{1}dx\frac{\log^{4}{x}\log{(1-x)}}{1-x}=12\zeta(3)^{3}-18\zeta(6)
\end{equation}
以下の式を証明せよ。
\begin{equation}
\zeta(2,4)=\frac{2}{3}\zeta(3)^{2}-\frac{4}{3}\zeta(6)
\end{equation}
また、$\zeta(2)\zeta(4)=\zeta(2,4)+\zeta(4,2)+\zeta(6)$より
\begin{equation}
\zeta(4,2)=\zeta(2)\zeta(4)-\frac{2}{3}\zeta(3)^{2}+\frac{1}{3}\zeta(6)
\end{equation}
を証明せよ。
[1]まずは前提になる式を書きます。
\begin{equation}
\int_{0}^{1}\frac{(\log{x})^{m}}{1-x}dx=(-1)^{m}m!\zeta(m+1)
\end{equation}
この式の証明は簡単なので省略いたします。
[2]次に$m=2$として二乗を計算します。
\begin{eqnarray}
\{\int_{0}^{1}\frac{(\log{x})^{2}}{1-x}dx\}^{2}&=&4\zeta(3)^{2}\\
&=&2\int_{0}^{1}\frac{(\log{x})^{2}}{1-x}dx\int_{0}^{x}\frac{(\log{y})^{2}}{1-y}dy\quad(z=\frac{y}{x})\\
&=&2\int_{0}^{1}\frac{x(\log{x})^{2}}{1-x}dx\int_{0}^{1}\frac{(\log{xz})^{2}}{1-xz}dz\\
&=&2\int_{0}^{1}\frac{x(\log{x})^{4}}{1-x}dx\int_{0}^{1}\frac{1}{1-xz}dz+4\int_{0}^{1}\frac{x(\log{x})^{3}}{1-x}dx\int_{0}^{1}\frac{\log{z}}{1-xz}dz+2\int_{0}^{1}\frac{x(\log{x})^{2}}{1-x}dx\int_{0}^{1}\frac{(\log{z})^{2}}{1-xz}dz\\
&=&-2\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx+4\sum_{n=0}^{\infty}\int_{0}^{1}\frac{x^{n+1}(\log{x})^{3}}{1-x}dx\int_{0}^{1}z^{n}\log{z}dz+2\sum_{n=0}^{\infty}\int_{0}^{1}\frac{x^{n+1}(\log{x})^{2}}{1-x}dx\int_{0}^{1}z^{n}(\log{z})^{2}dz\\
&=&-2\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx-4\sum_{n=0}^{\infty}\frac{1}{(n+1)^{2}}\int_{0}^{1}\frac{x^{n+1}(\log{x})^{3}}{1-x}dx+4\sum_{n=0}^{\infty}\frac{1}{(n+1)^{3}}\int_{0}^{1}\frac{x^{n+1}(\log{x})^{2}}{1-x}dx\\
&=&-2\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx+24\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\frac{1}{(m+n+2)^{4}(n+1)^{2}}+8\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\frac{1}{(m+n+2)^{3}(n+1)^{3}}\\
&=&-2\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx+24\sum_{m=1}^{\infty}\sum_{n=1}^{\infty}\frac{1}{(m+n)^{4}n^{2}}+8\sum_{m=1}^{\infty}\sum_{n=1}^{\infty}\frac{1}{(m+n)^{3}n^{3}}\\
&=&-2\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx+24\zeta(2,4)+8\zeta(3,3)
\end{eqnarray}
[3]ゆえに、以下の式を得る。
\begin{eqnarray}
\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx&=&12\zeta(2,4)+4\zeta(3,3)+2\zeta(3)^{2}\quad(\zeta(3,3)=\frac{1}{2}\{\zeta(3)^{2}-\zeta(6)\})\\
&=&12\zeta(2,4)+4\zeta(3)^{2}-2\zeta(6)
\end{eqnarray}
[4]実はまめひげさんの記事の定理7を参考にすると以下の式を得る。
\begin{eqnarray}
\int_{0}^{1}\frac{(\log{x})^{4}\log{(1-x)}}{1-x}dx&=&-60\zeta(6)+12\{\zeta(2)\zeta(4)+\zeta(3)\zeta(3)+\zeta(4)\zeta(2)\}\\
&=&24\zeta(2)\zeta(4)+12\zeta(3)^{2}-60\zeta(6)
\end{eqnarray}
ゆえに、以下の式を証明すればいい。
[5]$24\zeta(2)\zeta(4)-60\zeta(6)=-18\zeta(6)$
\begin{eqnarray}
\left\{
\begin{array}{l}
\zeta(2)=\frac{\pi^{2}}{6}\\
\zeta(4)=\frac{\pi^{4}}{90}\\
\zeta(6)=\frac{\pi^{6}}{945}\\
\zeta(2)\zeta(4)=\frac{7}{4}\zeta(6)
\end{array}
\right.
\end{eqnarray}
を用いると
\begin{eqnarray}
24\zeta(2)\zeta(4)-60\zeta(6)&=&42\zeta(6)-60\zeta(6)\\
&=&-18\zeta(6)
\end{eqnarray}
[6]以上をまとめると
\begin{eqnarray}
\left\{
\begin{array}{l}
\zeta(2,4)=\frac{2}{3}\zeta(3)^{2}-\frac{4}{3}\zeta(6)\\
\zeta(4,2)=\zeta(2)\zeta(4)-\frac{2}{3}\zeta(3)^{2}+\frac{1}{3}\zeta(6)
\end{array}
\right.
\end{eqnarray}
問題5⭐️⭐️
次の式が成り立つ事を示せ。
\begin{equation}
\{\frac{1}{(m+n-1)\begin{pmatrix}m+n-1\\m-1\end{pmatrix}}\}^{2}=2\sum_{k=0}^{n-1}(-1)^{k}\frac{\begin{pmatrix}n-1\\k\end{pmatrix}}{(k+m)(k+2m+n-1)\begin{pmatrix}k+2m+n-2\\n-1\end{pmatrix}}
\end{equation}
\begin{eqnarray} (\int_{0}^{1}x^{m-1}(1-x)^{n-1}dx)^{2}&=&2\int_{0}^{1}dx\int_{0}^{x}dy(xy)^{m-1}\{(1-x)(1-y)\}^{n-1}\quad(\frac{y}{x}=z)\\ &=&2\int_{0}^{1}dxx^{2m-1}(1-x)^{n-1}\int_{0}^{1}dzz^{m-1}(1-zx)^{n-1}\\ &=&2\sum_{k=0}^{n-1}(-1)^{k}\begin{pmatrix}n-1\\k\end{pmatrix}\int_{0}^{1}dxx^{k+2m-1}(1-x)^{n-1}\int_{0}^{1}dzz^{k+m-1}\\ &=&2\sum_{k=0}^{n-1}(-1)^{k}\frac{\begin{pmatrix}n-1\\k\end{pmatrix}}{k+m}B(k+2m,n)\\ &=&2\sum_{k=0}^{n-1}(-1)^{k}\frac{\begin{pmatrix}n-1\\k\end{pmatrix}}{k+m}\frac{(k+2m-1)!(n-1)!}{(k+2m+n-1)!}\\ &=&2\sum_{k=0}^{n-1}(-1)^{k}\frac{\begin{pmatrix}n-1\\k\end{pmatrix}}{(k+m)(k+2m+n-1)\begin{pmatrix}k+2m+n-2\\n-1\end{pmatrix}}\\ &=&\{\frac{1}{(m+n-1)\begin{pmatrix}m+n-1\\m-1\end{pmatrix}}\}^{2} \end{eqnarray}
問題6⭐️⭐️⭐️
テータ関数の類似物として次の様な関数を考える。
\begin{eqnarray}
\left\{
\begin{array}{l}
\vartheta_{3}({q})=\sum_{n\in\mathbb{Z}}q^{n^{3}}\\
\vartheta_{4,k}({q})=\sum_{n\in\mathbb{Z}}\omega^{kn} q^{n^{3}}\quad(k=1,2)
\end{array}
\right.
\end{eqnarray}
この様な関数を考えた時、以下の式を$\vartheta_{3}({q}),\vartheta_{4,k}({q})\quad(k=1,2)$で表せ。
\begin{equation}
\vartheta_{3}^{2}(q)+\vartheta_{4,1}^{2}(q)+\vartheta_{4,2}^{2}(q)
\end{equation}
ただし、$\omega$は$1$の三乗根とする。
[1]
以下$3$を法として計算した結果を羅列する。
\begin{eqnarray}
\left\{
\begin{array}{l}
0^{3}\equiv 0\\
1^{3}\equiv 1\\
2^{3}\equiv 2
\end{array}
\right.
\end{eqnarray}
この結果を用いると以下の式を得る。
\begin{eqnarray}
\left\{
\begin{array}{l}
\vartheta_{3}(\omega q)=\vartheta_{4,1}(q)\\
\vartheta_{3}(\omega^{2} q)=\vartheta_{4,2}(q)\\
\vartheta_{3}(q)+\vartheta_{4,1}(q)+\vartheta_{4,2}(q)=3\vartheta_{3}(q^{27})\\
\cdots
\end{array}
\right.
\end{eqnarray}
[2]以下次の様に記号を定める。
\begin{equation}
r_{3}(n)=\#\{(k,l)\in\mathbb{N}^{2}|k^{3}+l^{3}=n\}
\end{equation}
\begin{eqnarray}
\vartheta_{3}^{2}(q)=1+\sum_{n=1}^{\infty}r_{3}(n)q^{n}
\end{eqnarray}
これから、$q\rightarrow \omega q,q\rightarrow \omega^{2}q$として足し合わせる事で、以下の式を得る。
\begin{equation}
\vartheta_{3}^{2}(q)+\vartheta_{4,1}^{2}(q)+\vartheta_{4,2}^{2}(q)=3\{1+\sum_{n\in\mathbb{N}}r_{3}(3n)(q^{3n}+q^{-3n})\}
\end{equation}
また、次の恒等式:
\begin{equation}
(k+l)^{3}+(k+\omega l)^{3}+(k+\omega^{2}l)^{3}=3(k^{3}+l^{3})
\end{equation}
を用いたいところだが...
[3]
$k+\omega,k+\omega^{2} l\not\in\mathbb{N}$なので、$r_{3}(n)\neq r_{3}(3n)$。ゆえに、通常のテータ関数と同じ議論を行う事は出来ない。
そこで、別の方法を考える。
[1]の結果を用いると二つの自然数を用意し、それらの三乗の和を計算して$3$の倍数になるのは$3$を法として一方が$1$他方が$2$となる場合だけだと分かるので、$k,l$の入れ替えを考慮して以下の式を得る。
\begin{equation}
r_{3}(3n)=2\#\{(k,l)\in\mathbb{N}^{2}|(3k-2)^{3}+(3l-1)^{3}\}
\end{equation}
[4]
実は少し考察してみると以下の式が成り立つ事が分かる。
\begin{eqnarray}
\left\{
\begin{array}{l}
\vartheta_{3}(q)+\omega\vartheta_{4,1}(q)+\omega^{2}\vartheta_{4,2}(q)=3\sum_{n\in\mathbb{Z}}q^{(3k-1)^{3}}\\
\vartheta_{3}(q)+\omega^{2}\vartheta_{4,1}(q)+\omega\vartheta_{4,2}(q)=3\sum_{n\in\mathbb{Z}}q^{(3k-2)^{3}}\\
\end{array}
\right.
\end{eqnarray}
ゆえに、
\begin{eqnarray}
3\sum_{n\in\mathbb{Z}}r_{3}(3n)q^{3n}&=&\frac{2}{3}\{\vartheta_{3}(q)+\omega\vartheta_{4,1}(q)+\omega^{2}\vartheta_{4,2}(q)\}\{\vartheta_{3}(q)+\omega^{2}\vartheta_{4,1}(q)+\omega\vartheta_{4,2}(q)\}\\
&=&\frac{2}{3}[\vartheta_{3}^{2}(q)+\vartheta_{4,1}^{2}(q)+\vartheta_{4,2}^{2}(q)-\{\vartheta_{3}(q)\vartheta_{4,1}(q)+\vartheta_{4,1}(q)\vartheta_{4,2}(q)+\vartheta_{4,2}(q)\vartheta_{3}(q)\}]
\end{eqnarray}
[5]結論
\begin{equation}
\vartheta_{3}^{2}(q)+\vartheta_{4,1}^{2}(q)+\vartheta_{4,2}^{2}(q)=9-2\{\vartheta_{3}(q)\vartheta_{4,1}(q)+\vartheta_{4,1}(q)\vartheta_{4,2}(q)+\vartheta_{4,2}(q)\vartheta_{3}(q)\}
\end{equation}
