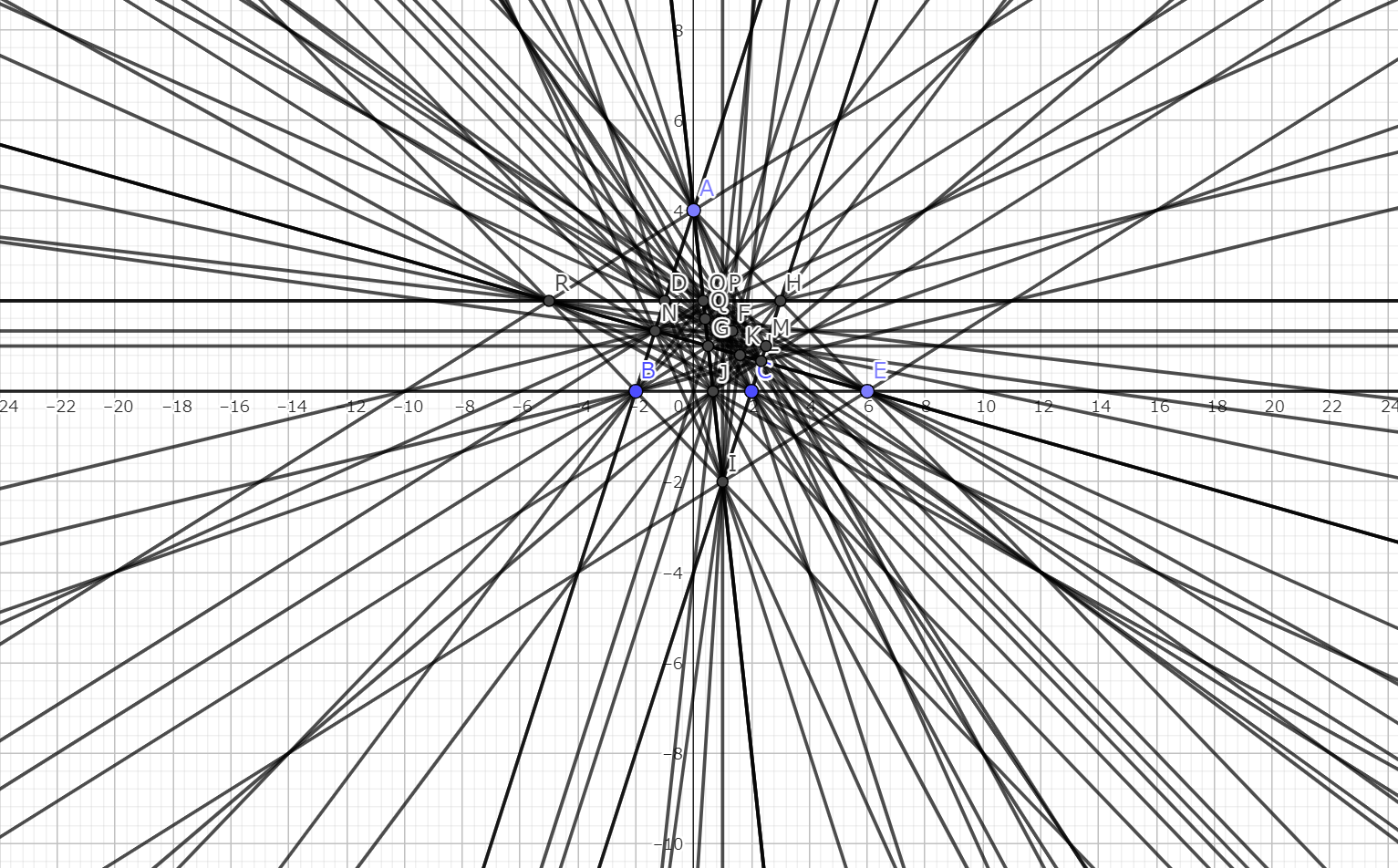
Kobon TriangleをMenelausとつなげる
藤村の三角形問題 の考察をしている際に、気づいたことがあったのでまとめます。
導入
平面上に k 本の直線を引くときに重なり合わずに作ることのできる三角形の最大数は何個か
この問題の解を一般化することなどは未解決であるが、部分的には証明されているものがある。(以下例)
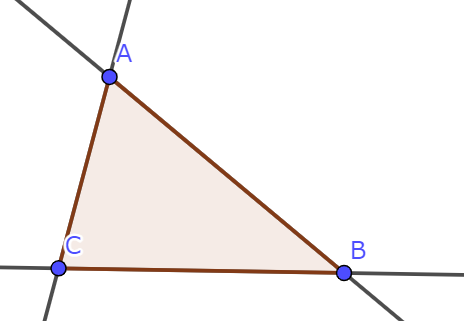 k=3のとき
k=3のとき
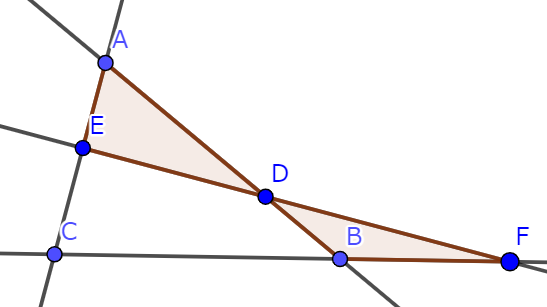 k=4のとき
k=4のとき
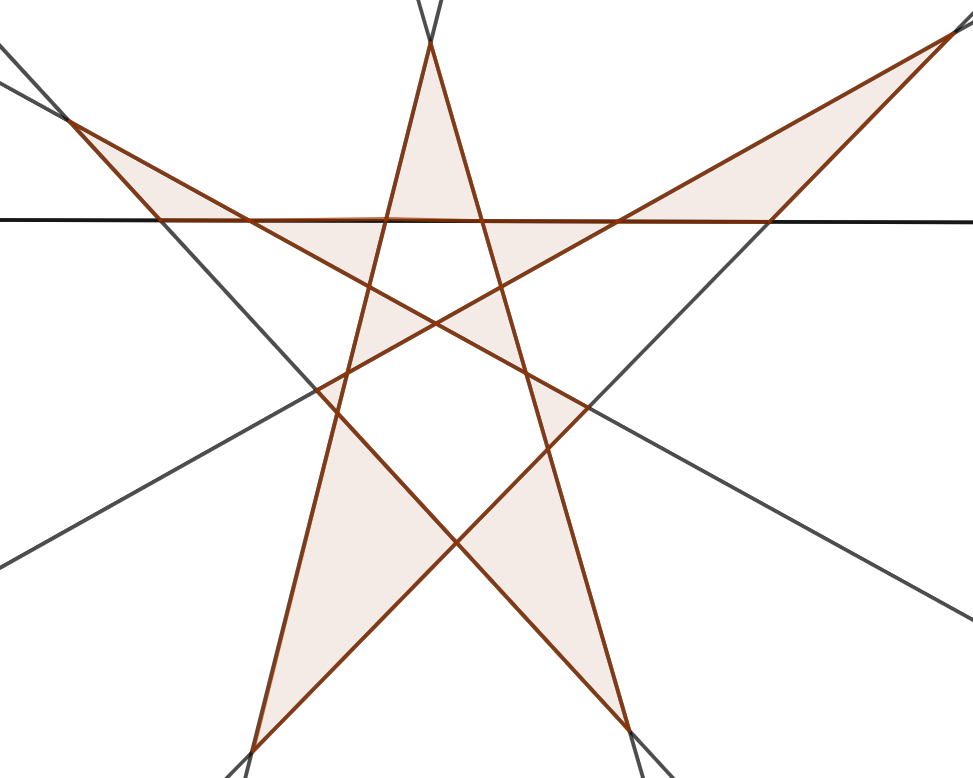 k=7のとき
k=7のとき
※詳しく知りたい方は こちら を参考にしてください。
(座標)平面上で、n本の直線に囲まれて出来る図形。ただし、今回は図5においての内部領域を三角形ADC内とする
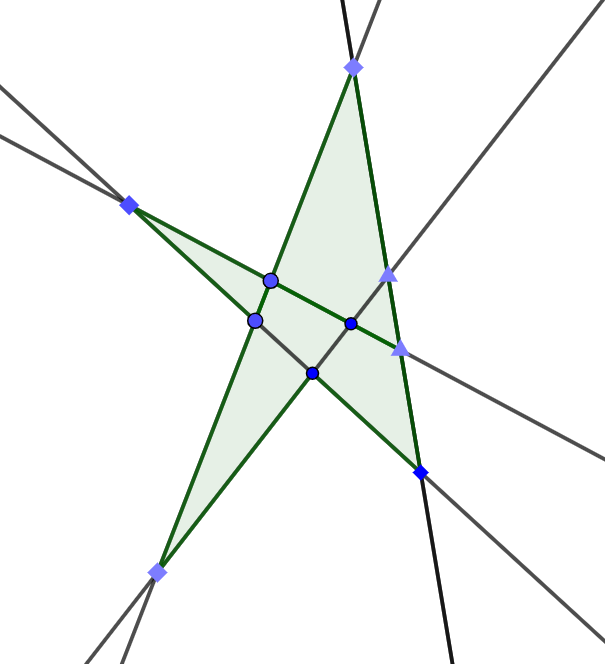 内部領域
内部領域
本題
この問題について、様々な図形を描いていた時にk=4の形がMenelausの定理を思い出させるような形をしているなと思い関係性があるのか気になった。そこで、以下の操作について考えることにした。(言葉だけではわかりにくいので枠組みの下に図を載せます)
Menelaus Rule
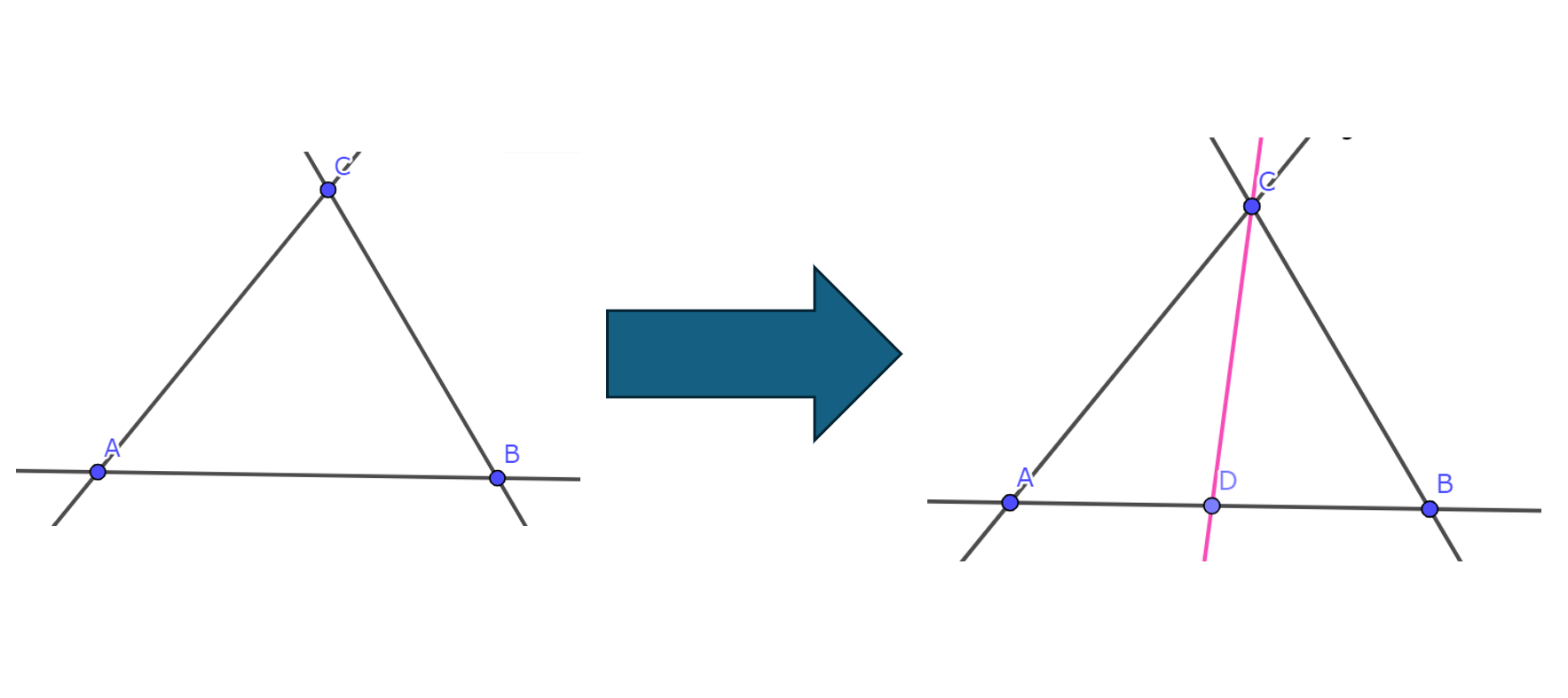
操作1:Menelausの定理が成り立つ図形を書く(線分を直線にする)
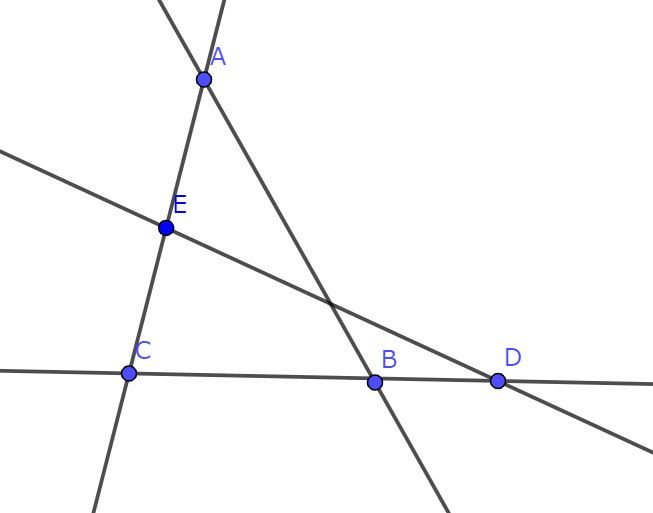 操作1
操作1
操作2:操作1において三角形ABC及び線分ADとの交点(法則性がより難しくなるためにDも含む)から点A,B,Cに向かって直線を引く。
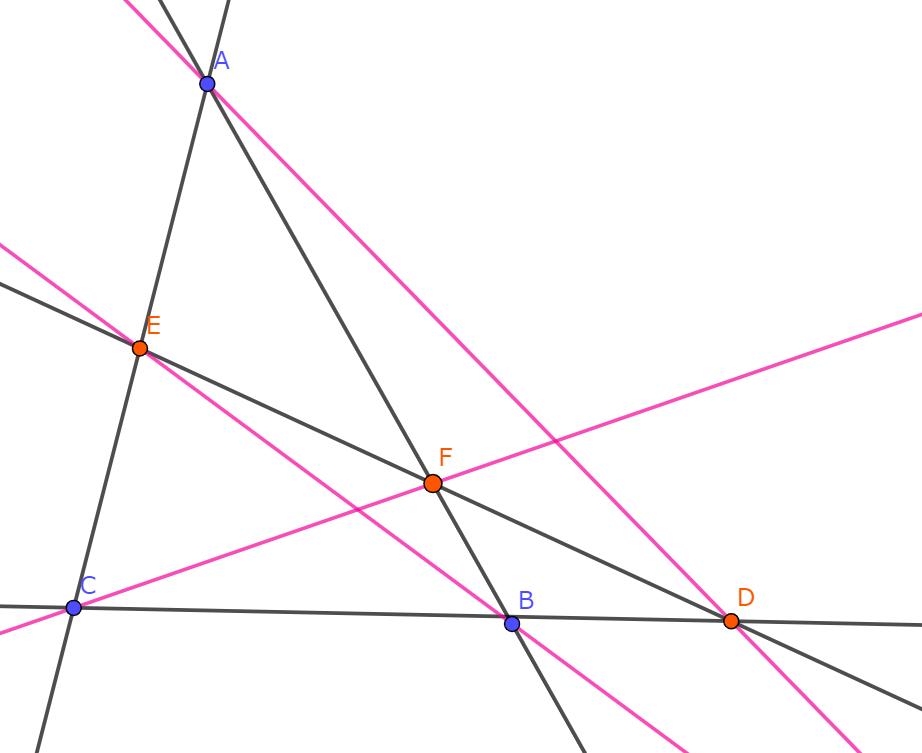 操作2
操作2
操作3:新たにできた交点(内部領域内における)から操作2と同じ操作をする。
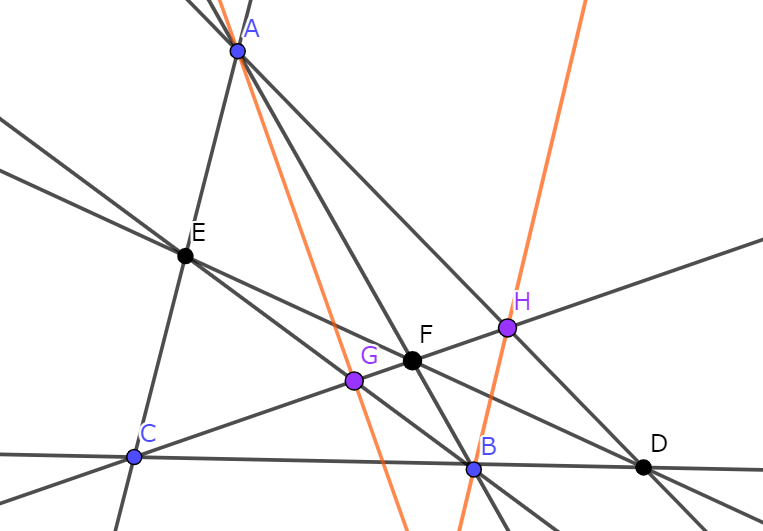 操作3
操作3
操作4:以上を繰り返す
この操作をすることで、内部領域内で生成される図形がほとんど三角形である!!
最初に図7の図形を見たとき私は以下の予想を立てた。
以上の操作において生成される図形はすべて三角形である。
実際は操作4において反例が現れるのでこの予想は正しくないことが分かった。しかし、これだけ三角形が生成されるのには何か性質があるのではないかと思い研究することにした。
この図形の中には藤村の三角形において最適解を示すものが存在する。
k=4のとき満たすことが分かっている。
それ以外ではどうか?
おそらく、K>4では得られないと考えられる。
具体的に考えるために、図7から考察していると
のようにピンク色の線によって三角形が2分割されているものが多くみられることが分かった。
このとき、内部領域的には線分を一本損することになり、別の三角形に使われる場合と比べても、総線分数的にも損する。[1]
つまり、perfect configurationに比べて、これは三角形の個数も少なくなる。
以上より、k>4の場合においてはこれが最適解となることは存在しにくいということが言える。
(厳密な証明ではないけれども感覚的にはこのように解釈しました)
最適解について考えるうえで一部の例外を除くと基本的には、3直線が1点で交わらない、どの2直線も平行でないという環境下で検出されている。(無駄なく三角形を生成できるため)そのため、今回のように3直線が1点で交わるということを許容したものでは、三角形を作るための特別な状態で考えていることになるのでたくさん出てきたのではないか?
実験
Menelausの定理のように操作1の段階において比を変えることによって新たな性質が見えるようになる。
以下、geogebraを用いて具体的に考察をしてみた。
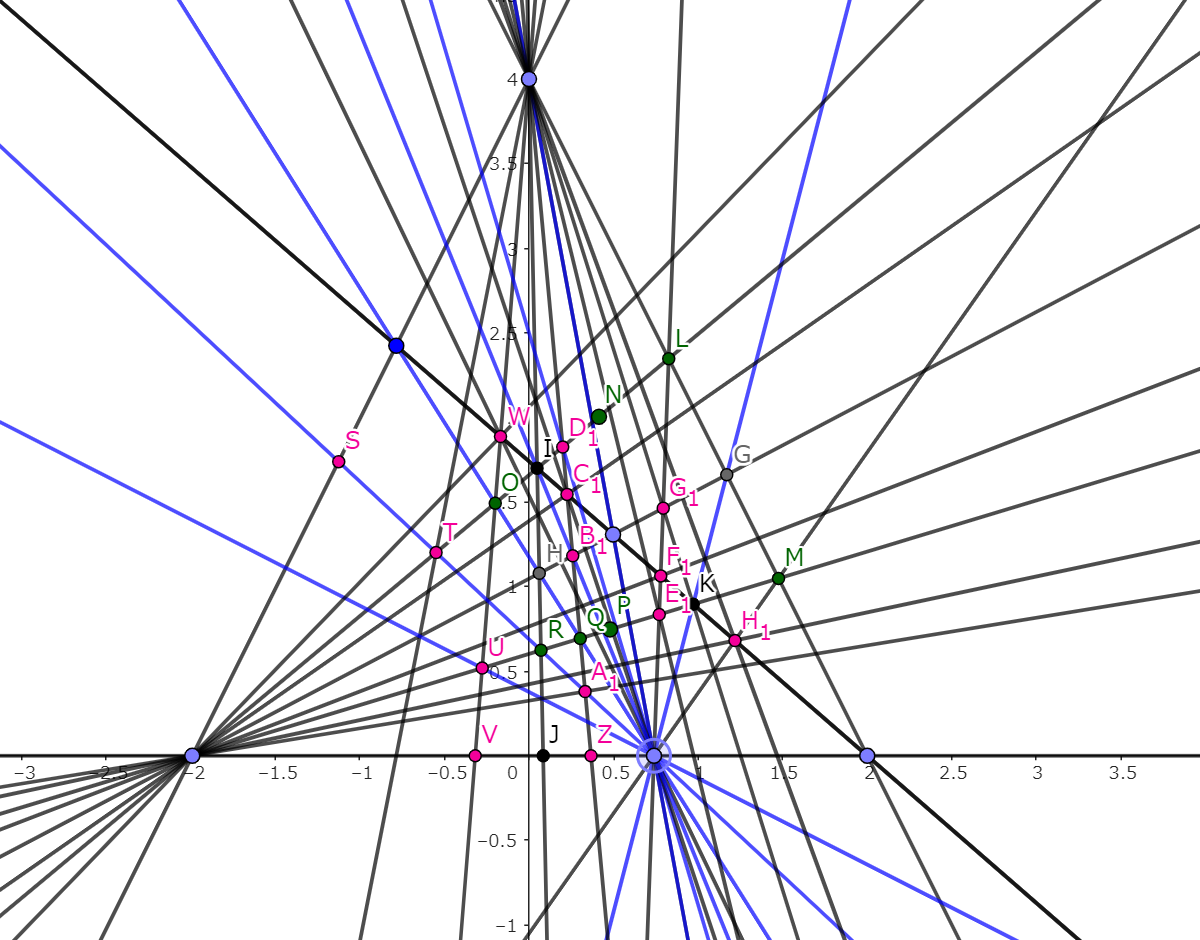
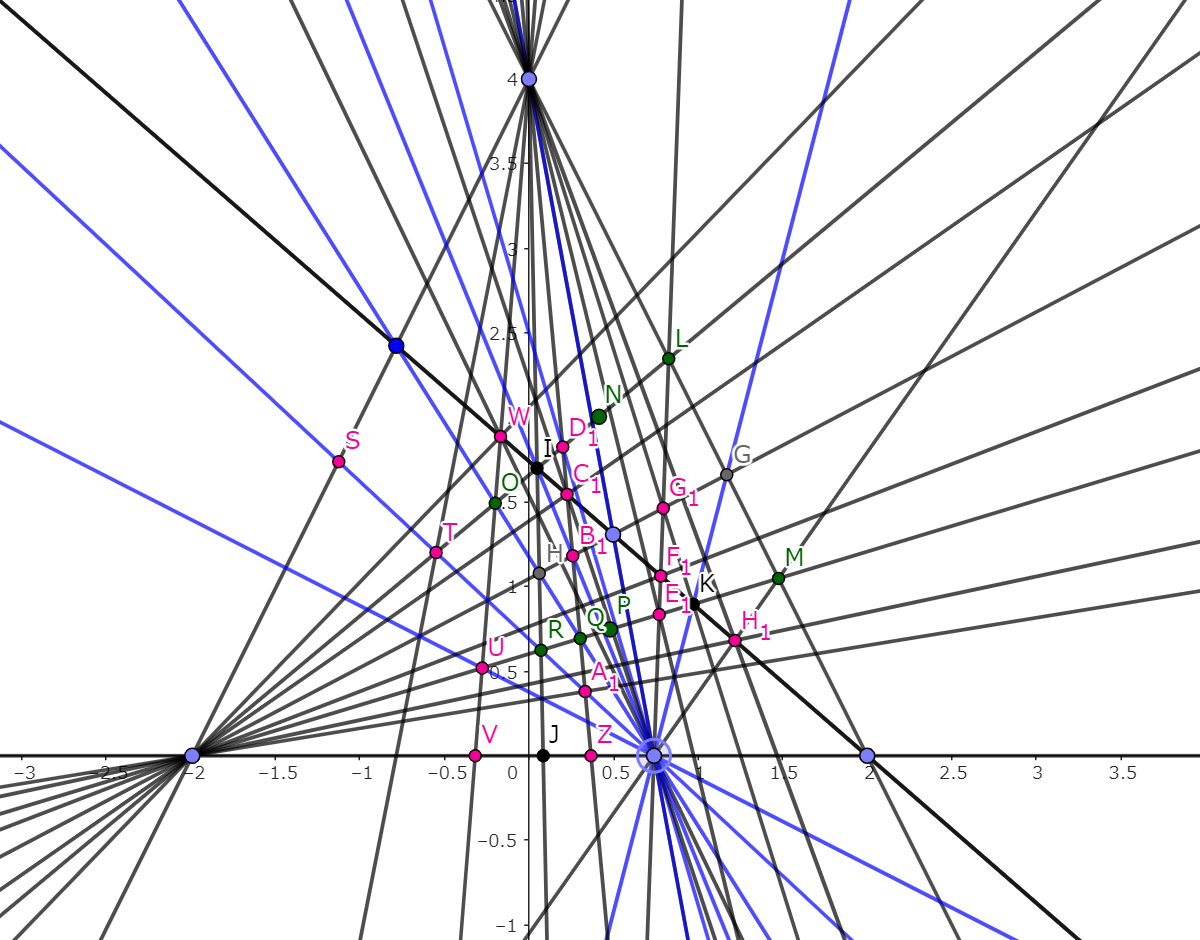
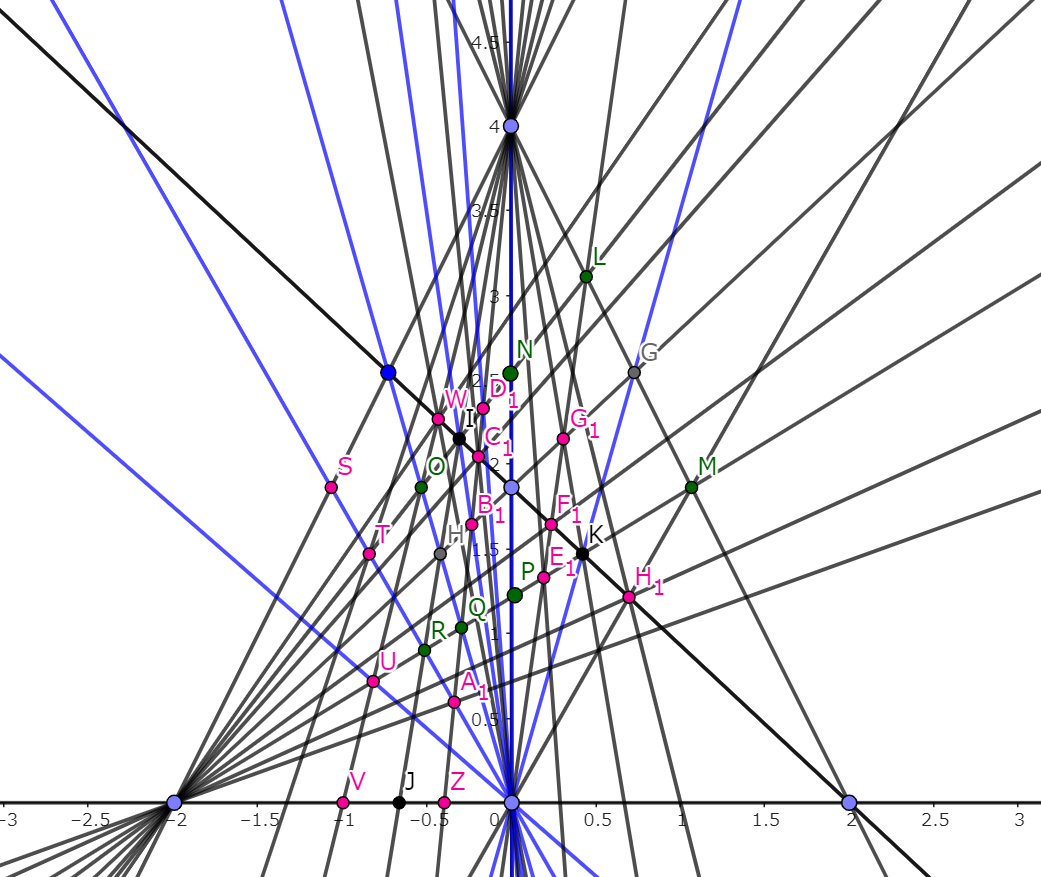
以上のように、いずれの場合においても現れる図形はどの場合においても同じであり、個数も同じである。(つまり図形の形が多少変わるくらいしか変化が起こらない!)
これがなぜ起こるのかというと、もともとこの図形において動点となるのはおおもとの三角形のみであり、それ以外の点は定点となることで線分比を変えたとしても、図形としての情報(三角形、四角形など)は失われることはないからである。
つまり、以下の補題が成り立つといえる(自明な部分はあるため性質として気づいたもの)。
動点からあるルールに従って引かれたものは、定点となり図形としての一般性は失われない
この補題を活用することによって要旨集にもあるような下界をより厳密なものにすることができると予想した。
※私のプロフィールのアイコンはMenelausRuleの操作を繰り返していたときに現れたものです。