文献あり

Hydra(6)<BH(3)<Hydra(7)の証明

きっかけ
ブーフホルツのヒドラ -巨大数学wikiによると、
こうかかれてある。
勘違いしうる文脈
この内容から、BH(3)はTREE(3)やSCG(3)を超えるように思えるが、実際はそんなことはない。
ブーフホルツのヒドラはこのように定義される。

① 用語の定義
用語の定義

②ルール
ターンごとに、ヘラクレスはヒドラの首を1つ選び、それを切り落とす (グラフから除去する)。現在のターン数をnとして、選んだヒドラの首と現在のターン数に応じて、ヒドラは以下の規則に応じて変形する。
切った頭のラベルが0である場合。この時はヒドラゲームと同様にする。すなわち,
切った首の根本が根である場合、首は生えてこない。
切った首の根本が根でない場合、親首から上側のコピーが、親首の根本から本新たに生える。

切った頭のラベルが0でない自然数u+1である場合。
ラベルがu以下である、切った頭から根に向かって最初の頂点をpとする。また、頂点pのラベルをvとする。
ヒドラのpから上の部分をSとする。Sでpにあたる頂点のラベルをuにして、切った首が生えていた場所にラベルが0の頭を生やしたものを、元のヒドラの切った首の根本から生やす。

切った頭のラベルがωである場合、切った首の根本からラベルがn+1である頭が生える。

③関数の定義
+、0、ω、ω…ωのように、ラベルのついたn個の頂点が並んだ木について、右端から首を切断していき、全ての首を切断するのにかかるターン数をBH(n)とする。また、+、0、0、0…0のように、ラベルのついたn+1個の頂点が並んだ木について、右端から首を切断していき、全ての首を切断するのにかかるターン数をHydra(n)とする。
小さい値を列挙すると、
BH(1)=Hydra(0)=0
BH(2)=Hydra(1)=1
Hydra(2)=3
Hydra(3)=37
となる。ここで、Hydra(n)関数は急増化関数を用いて、Hydra(n)∽fε_0(n)と評価される。
詳しくは、ふぃっしゅ数バージョン5を参照すること。

ある木の構造Aについて、現在がnターン目のときに、首を全て切り落とすのがA(n)となるように、A(n)を定義する。

単調性

ある木AとBについて、AがBを含むならば、A(n)>=B(n)

A=Bのときは自明だから、A≠Bの場合を証明する。
A,Bを順に切断した際、AとBの構造が異なる部分を切断する時AはBよりも多く切断し、
その後AはBと一致する。そのためA(n)>B(n)が成立し、証明完了。

上位変換

ラベルが0のある頭について、そこから伸びる頭のうちもっと左のものがラベルが1のもの単体で、それ以外が
全てラベル0の頭のみで構成されるとき、そのラベル1の頭をラベル0の2連続に変換した後の木をB,ラベル0の2連続と1連続の2つに変換した後の木をCとして、
C(n)>A(n)>B(n)となる。
特に、その頭が全体の最も右端のとき、
A(n)=B(n+1)

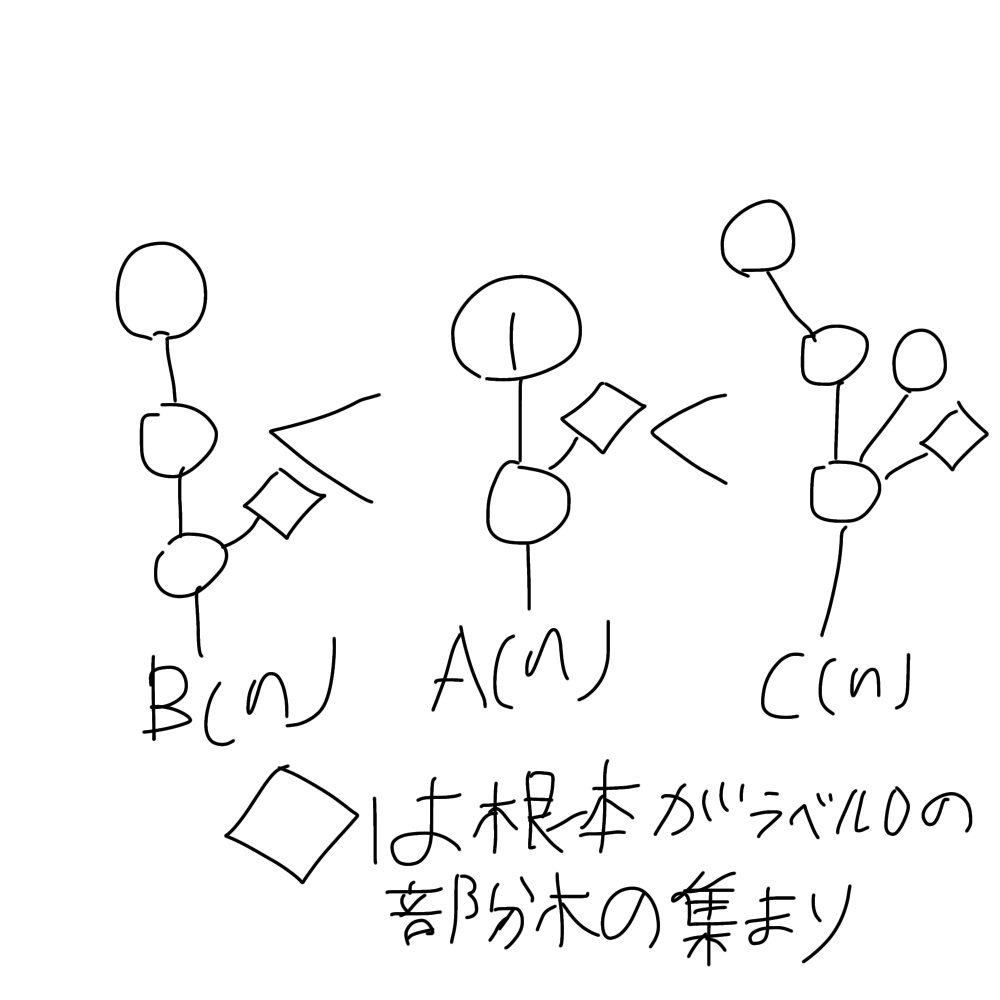主張

A,B,Cを順番に切断すると、構造が異なる部分を切断する際
切断回数が変わるのが、図と補題1より分かる。ひし形の意味についてだが、ひし形の根元が1の場合、この構造が複製されるので、
ひし形は、この構造が複製されないなら何でも良い。この場合、ひし形がない形複数個に帰着でき、帰納的に証明可能だ。
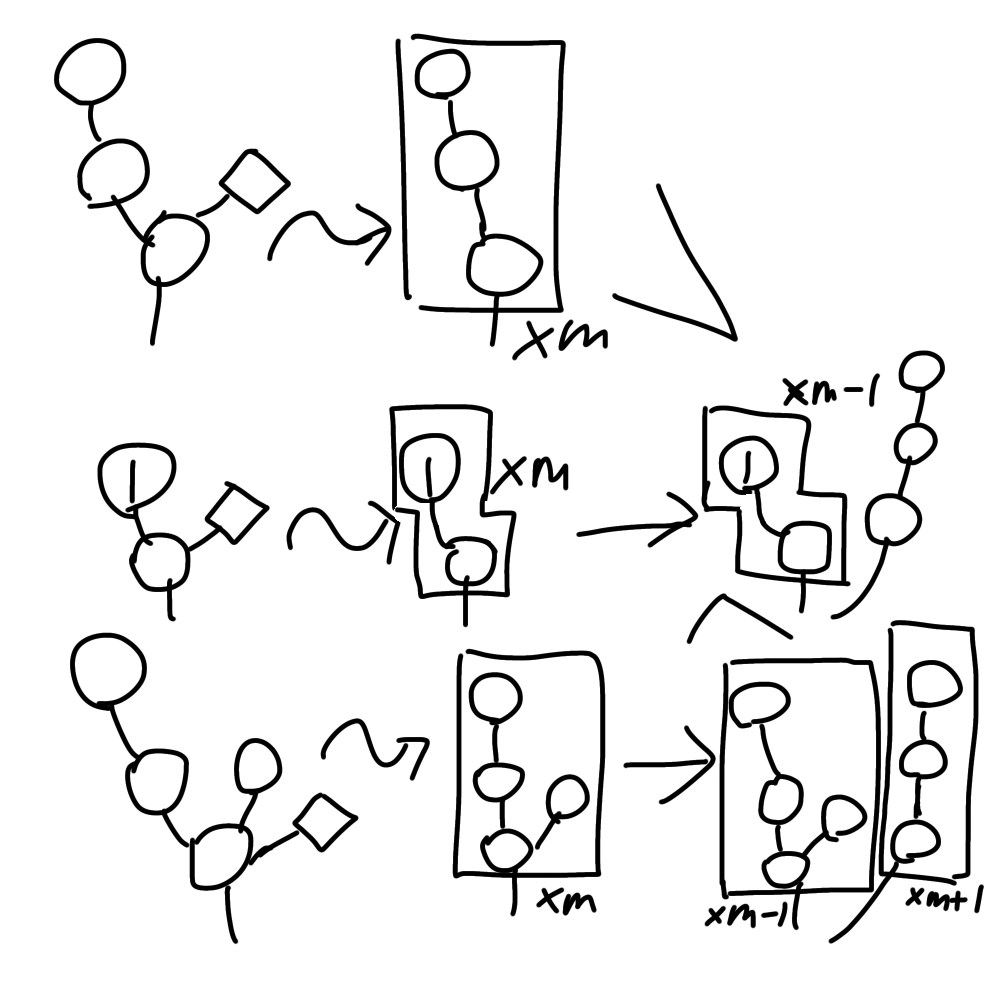証明

図5の通り
証明の流れは補題2と同じ。

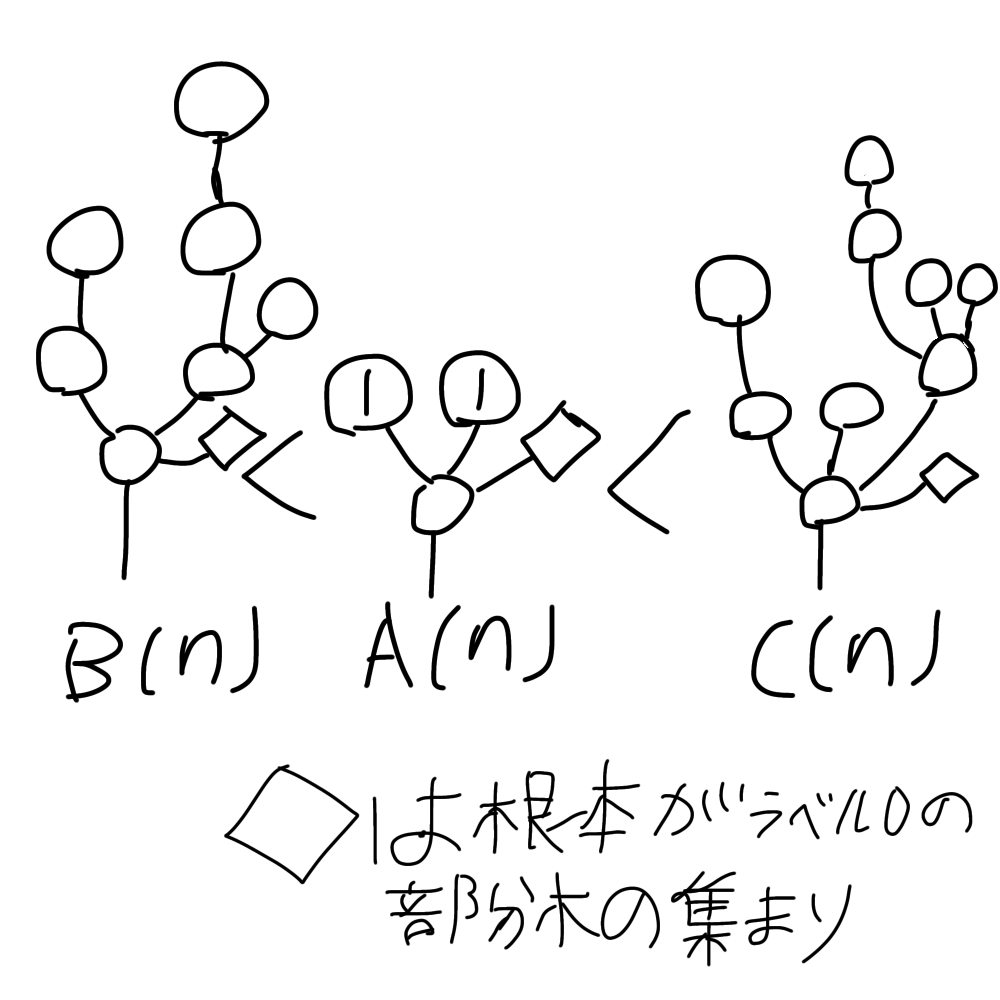主張

図6の通り
証明の流れは補題2と同じ。

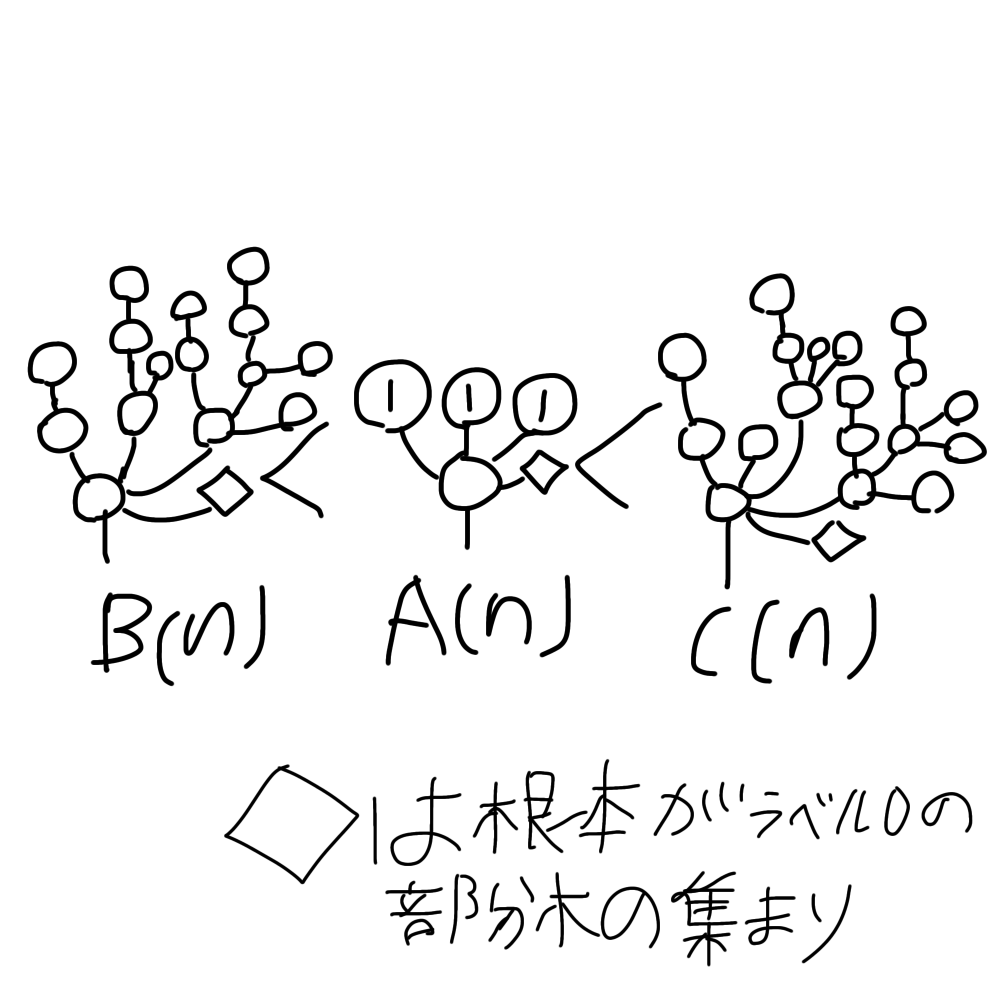主張

ここから本題に入る。
構造を上から、C,B,AとしてC(n)>B(n)>A(n)が補題1,4より分かる。
ここでHydra(6)の初期配置をAは含むため(青枠)、補題1よりBH(3)>Hydra(6)
Hydra(7)の初期配置を変形していくと、どこかでCを含むため、
補題1よりBH(3)<Hydra(7)
題義は示された。

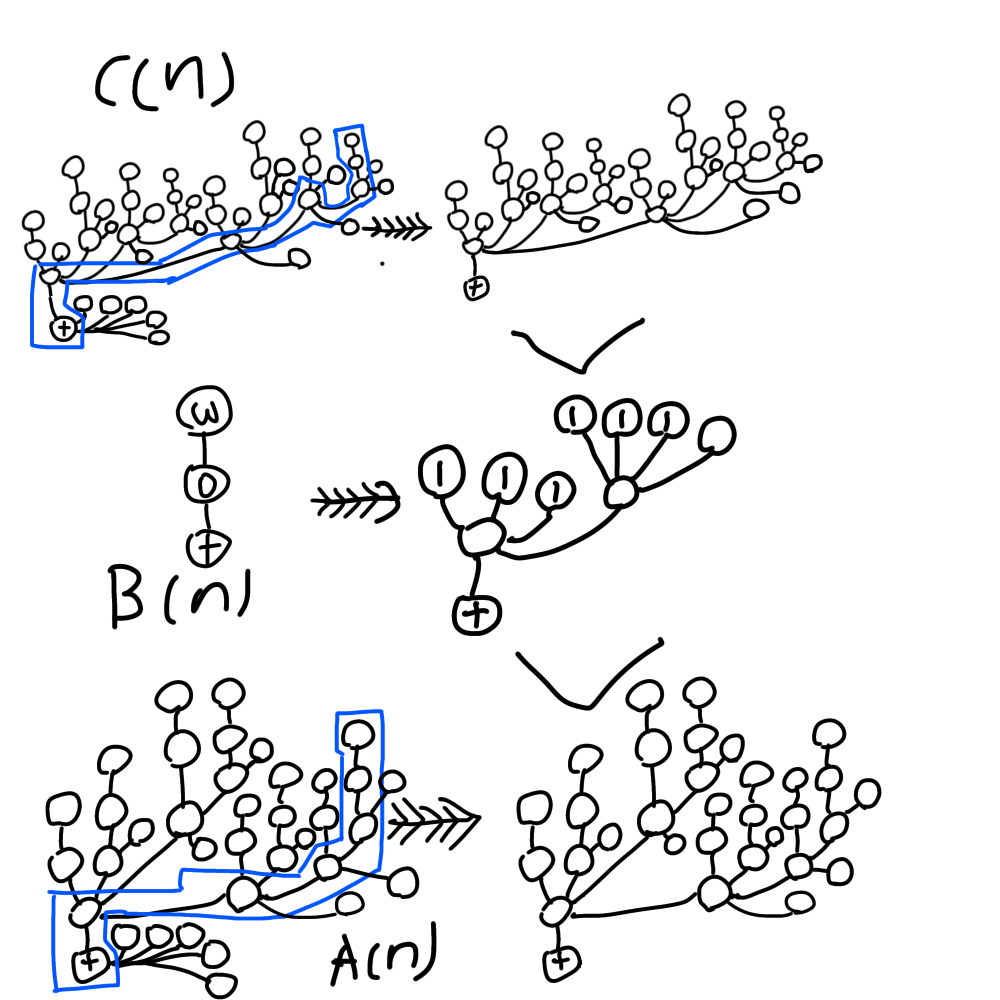証明の流れ

BH(3)の評価
fを急増加関数とする。
図6について、AとCでは、Aの方が近似精度が高い。このとき青枠部分が支配的であり、
その左側はほとんど無視できる。Hydra(6)はふぃっしゅ数バージョン5に登場するm(n)変換で高い精度で下から抑えることができ、
それは(m(4))^4(m(5))^2m(4)m(3)m(2)f(5)と表せ、正確にf_ω^ω^(ω*2-4)(5)と一致する。(Hydra(6)を初期局面から3回変形してこの評価を得る。)
Aはもう少し強い近似によって、
m(2)m(3)m(4)m(6)m(5)m(4)m(3)m(2)f(7)が得られる。
これは正確にf_ω^(ω^(ω^ω+1)+1)+1(7)である。
BANを用いて近似すると、{7,7,2[2[2]2]1,2}
これが、求めていたBH(3)の近似値だ。