とある自作問題の解説

はじめに

　こんにちは。今回は先日の柏陽祭に寄贈させていただいた問題の解説をしていきます。図から作った問題なので，割と再現性のある解法になっていると思います。

問題

　図はこんな感じです。
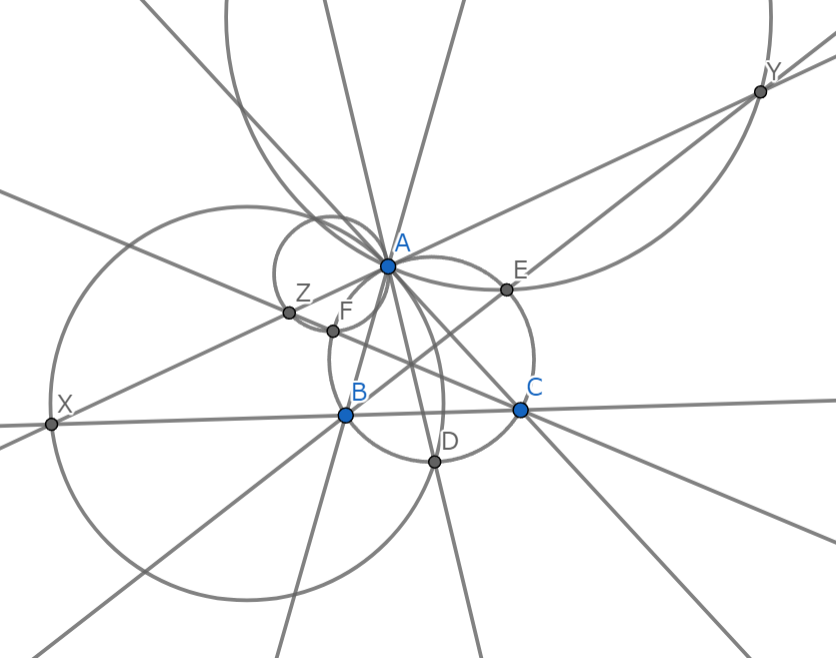問題図

$$ \text{― ネタバレ防止用空白 ―}$$
$$ \text{解説は例によって位置関係の議論がガバガバです}$$

解答

　"共軸である～" をわざわざ "外心が同一直線上にある～" って書く文化嫌じゃないですか？私は嫌です。

　対称性のつき方的に円$AEY$と円$AFZ$の交点を$P$とし，これが円$ADX$上にあることを示すのがよさそうです。

解法1.（writer解）

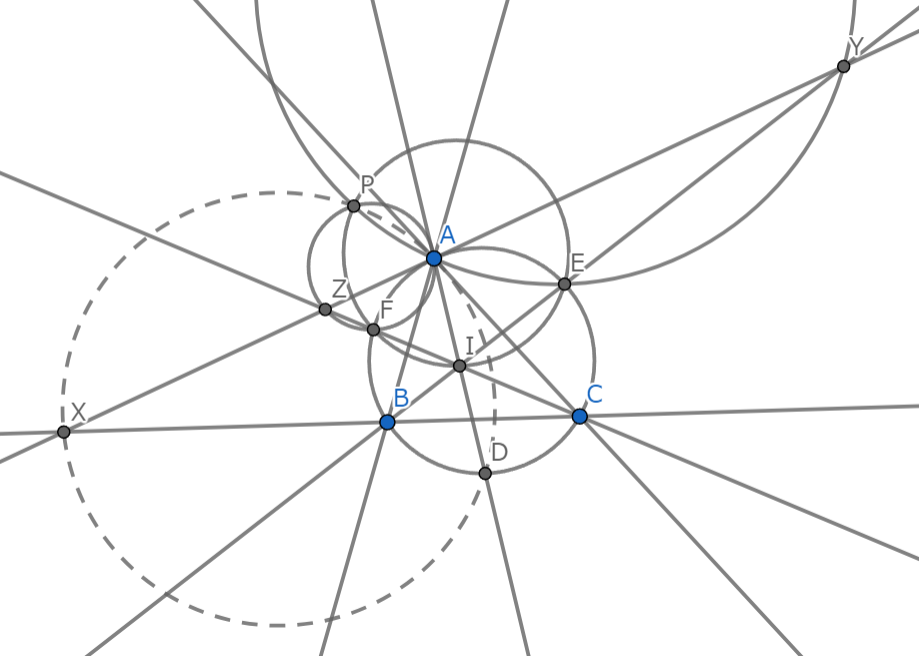解説図1-1

　まず，$\triangle ABC$の内心を$I$とすると
$$ \angle EPF=\angle EPA+\angle APF=\angle IYA+\angle AZI=180^\circ-\angle EIF$$
から$I,E,F,P$が共円であることが分かります。

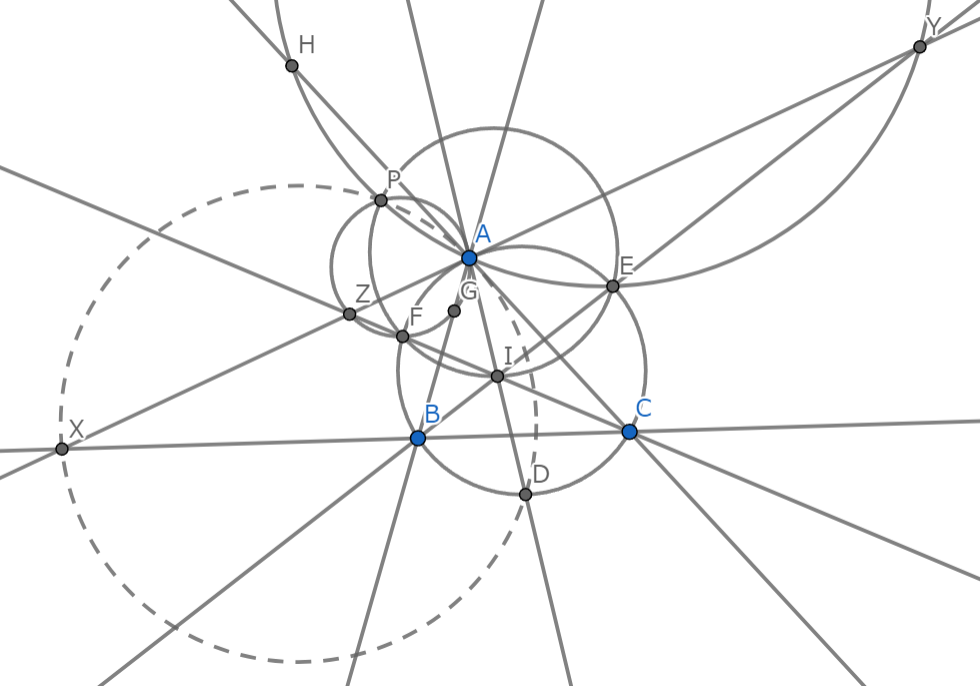解説図1-2

　また，円$AFZ$と$AB$の交点を$G$とすると，
$$ \angle AGZ=\angle AFZ=180^\circ-\angle AFC=180^\circ-\angle ABC=\angle ABX$$
であるから$GZ\parallel BC$であることが分かります。parallelの綴りは分かりませんでした

　同様に円$AEY$と$AC$の交点を$H$とすると$HY\parallel BC$であることが分かります。

　さて，図を眺めていると$H,P,G,I$が共線っぽいことに気づきます。これは非自明ですが，先ほどの$GZ\parallel HY\parallel BC$を使うモチベで考えると，
\begin{align} \angle APG&=\angle APZ-\angle GPZ \\ &=180^\circ-\angle AGZ-\angle GAZ \\ &=180^\circ-\angle ABX-\angle BAX \\ &=\angle ABC-\angle BCA \end{align}
および
\begin{align} \angle API&=\angle APF-\angle IPF \\ &=\angle AZI-\angle BCI \\ &=180^\circ-\angle IAX-\angle AIZ-\angle BCI \\ &=180^\circ-\left(\angle ACB+\frac12\angle BAC\right)-\left(\frac12 \angle BAC+\frac12\angle ACB\right)-\frac12\angle ACB \\ &=180^\circ-2\angle BCA-\angle BAC\\ &=\angle ABC-\angle BCA \end{align}
より$G$が$IP$上にあることがわかり，同様のことが$H$についてもいえるので示されます。（上の角度計算はもっと簡潔にできそうです）

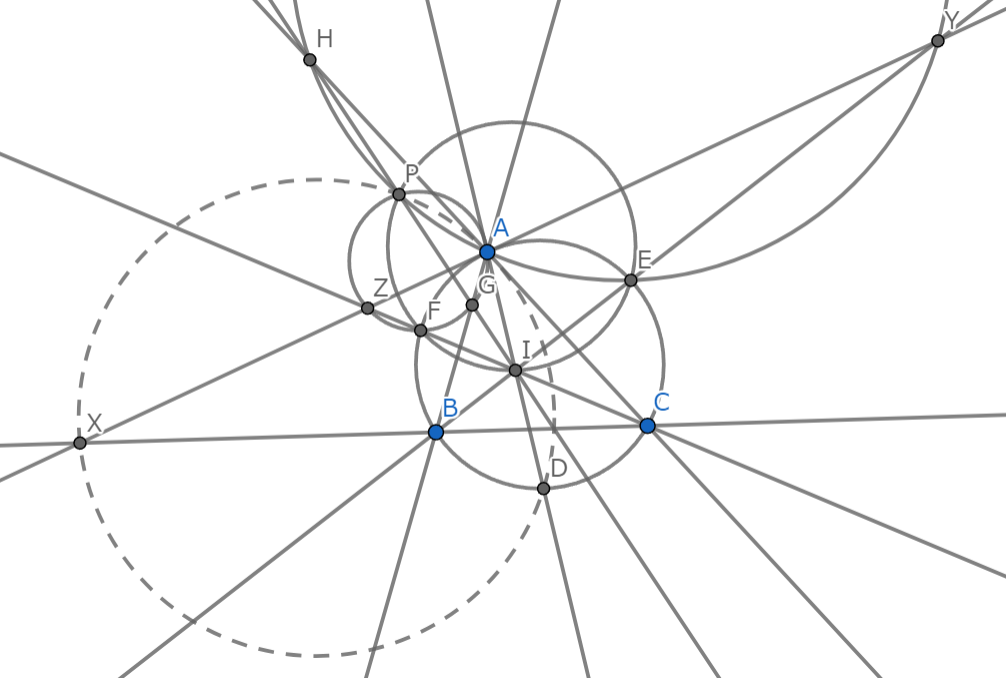解説図1-3
　さて，直線$HPGI$を図に書いてみました。なんか$BC$と$HPGI$の交点も点線の円上にありそうに見えませんか？

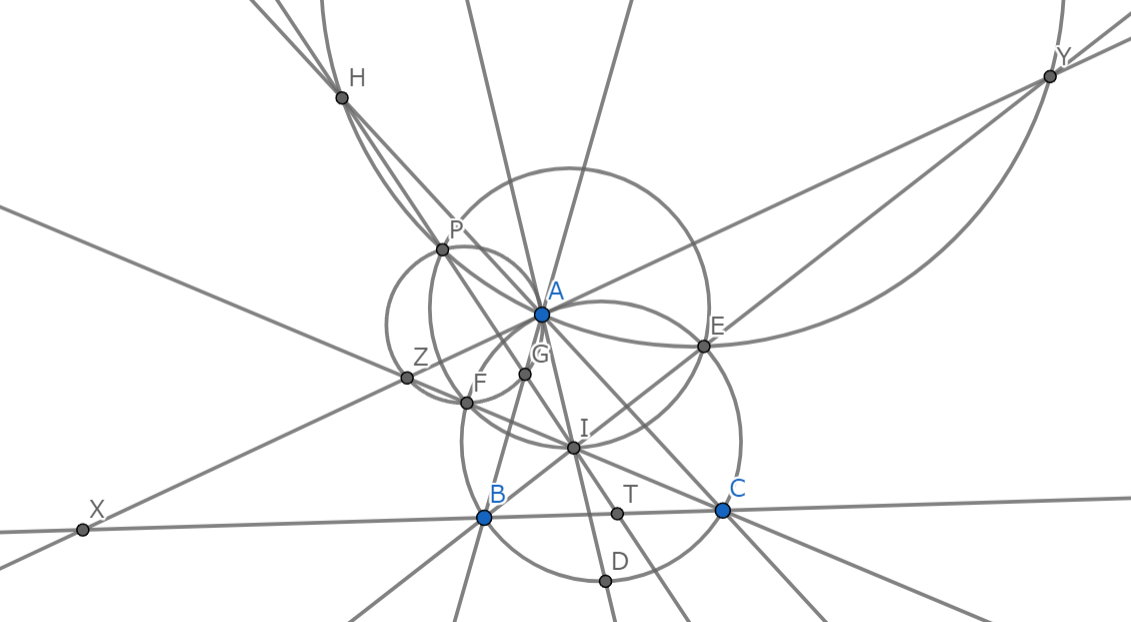解説図1-4
　ということでこの点を$T$として，$A,P,X,D,T$が共円であることを示していきましょう。

　ここで$\angle APT=\angle AZG=\angle AXT$より$A,P,X,T$が共円だとわかります（これが$T$を取った嬉しさ）。ですから（示しやすそうな）$A,X,T,D$の共円をいうことを考えます。

　ところで$AI$と$BC$の交点を$Q$とすると，$XA=XQ$が成り立ちます（典型です，簡単な角度計算で示せます）。ということは$DQ=DT$を示せば良いです。

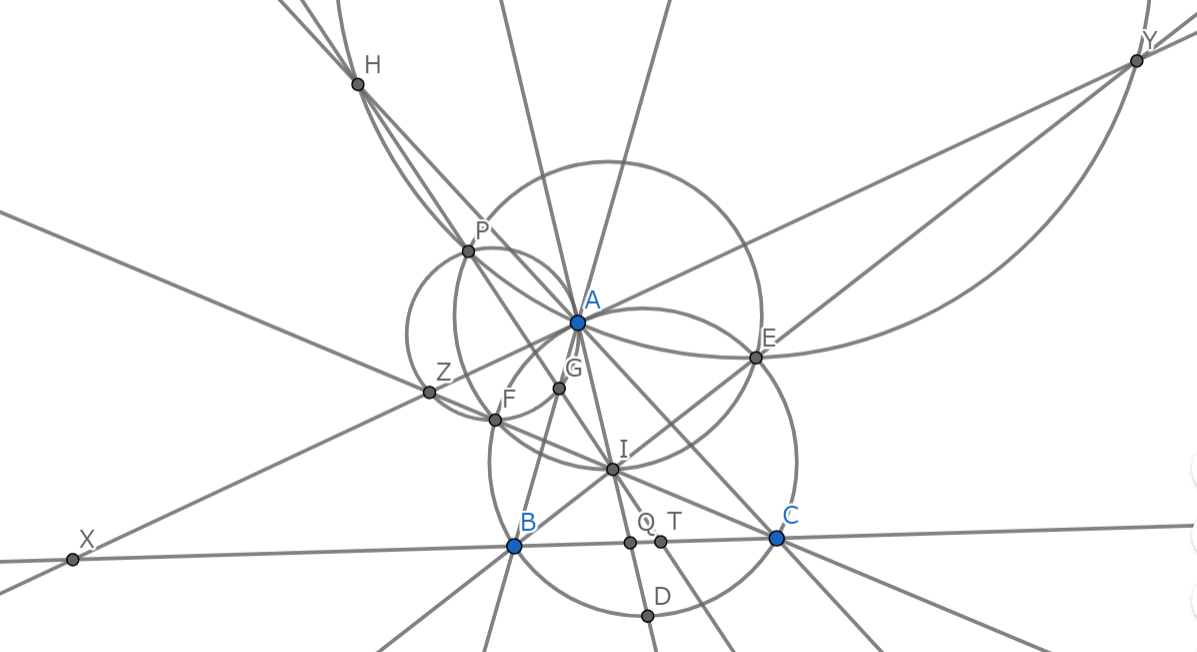解説図1-5

　$D$は弧$BC$の中点ですからこれは$BQ=CT$と同値です。対称性が微妙になくて気持ち悪いので$BT:TC=CQ:QB$を示します。$CQ:QB=AC:AB$ですし，共点とか平行とかが無限にあるので適当に計算すれば行けそうですね，やります。

　まず
$$ BT=YH\times\frac{TI}{IH}=XC\times\frac{HA}{AC}\times\frac{TI}{IH}=XC\times\frac{TQ}{QC}$$
がわかり（最後はメネラウスです），同様に$CT=XB\times\dfrac{TQ}{QB}$が分かります。よって$BT:CT=XC\times BQ:XB\times CQ$です。これが$CQ:BQ$と等しいことをいえばいいですが，これは$\triangle XAB\sim \triangle XCA$より$XB:XC=AB^2:AC^2=BQ^2:CQ^2$であることから従います！

　というわけで解けました。やったぜ。

$$ \text{？？？「内心で反転したら一発やね」}$$

解法2.（tester解）

　内心で反転したら一発らしいです。やってみましょう。（いつか追記します） ※以下9/29追記

　まず内心で反転するとその内心は垂心と化すことが知られていますね。一応$AB>AC$になることに思いを馳せておくと図はこんな感じになります。

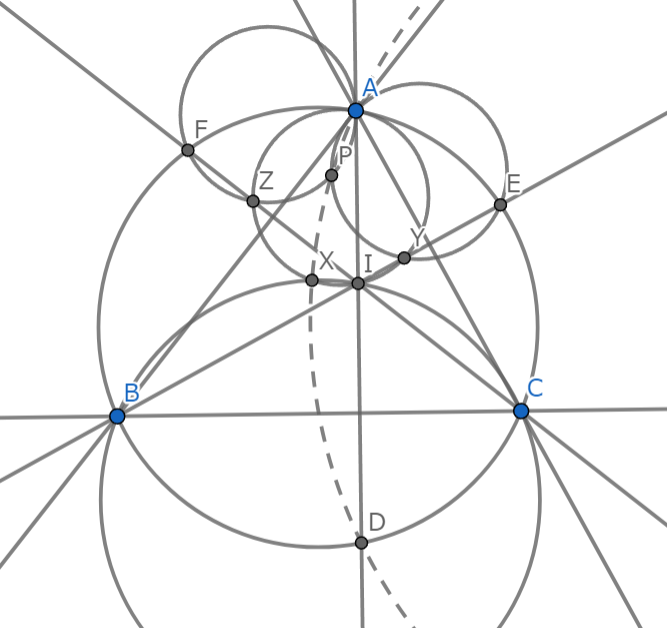解説図2-1

　まず，さっき$I,E,P,F$共円だったものが$E,P,F$共線に変わっているのでこれを示しておきましょう．$\angle EPA=\angle EYA=180^\circ-\angle AZF=180^\circ-\angle APF$なのでOKですね．

　$X$がめっちゃミケル点っぽい見た目だな～と思いながら図を見ていると，$\triangle BCD\sim \triangle YZP$で，その中心が$X$っぽい感じがします。というか，$ID$と円$IBC$の交点を$T\ (\neq I)$としたら$J$と$A$がこの相似に乗っていそうな気がしてきます。これを示したいです。

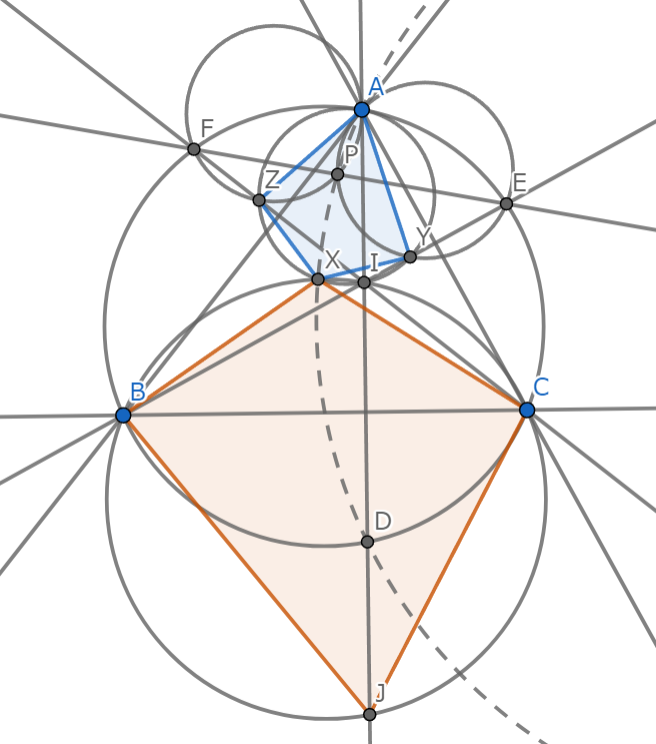解説図2-2

　とりあえず$P$が$\triangle AYZ$の垂心であることを示しましょうか。どう見ても雑に角度計算をしていけば行けそうな見た目をしているので，やります。

\begin{gather} \angle PAY=\angle PEY=\angle BCI=\angle DJB \\ \angle AYP=\angle AEF=\angle ACI=\angle IBA=\angle JBD \end{gather}

より$\triangle APY\sim\triangle JDB$が分かり，同様に$\triangle APZ\sim\triangle JDC$もいえるので示せました（厳密にはアウトですが有向角にすれば向きも言えます）。

　ということで次に$\triangle XBC\sim\triangle XYZ$を示します。これも適当にやれば行けそうな見た目をしていますね，

$$ \angle XYZ=\angle XIZ=\angle XBC$$

で，もう一つの方でも同じことが言えるのでOKです。

　これらをあわせて

「$\triangle BCD\sim \triangle YZP$で，その中心が$X$っぽい感じがします。というか，$ID$と円$IBC$の交点を$T\ (\neq I)$としたら$J$と$A$がこの相似に乗っていそう」

が正しいことが示せました。

　...最終的に示したかったのは$A,P,X,D$の共円ですよね，でもこれは↑から$\angle APX=\angle JDX$なので示せちゃってますね！

　めっちゃ楽に示せちゃいました。すごい。

おまけ（とある補題について）

　追記します