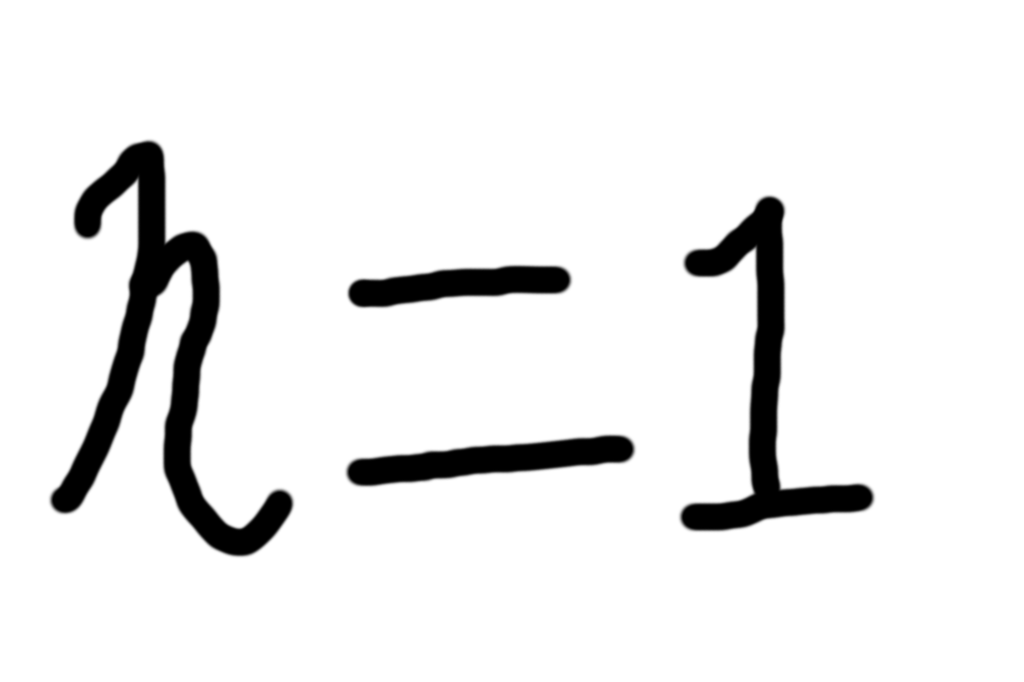x^x^x(xテトレーション3)の逆関数

はじめに

　こんにちは、久しぶりのn=1です。今回は$x^{(x^x)}$の逆関数、すなわち$^3x$(x テトレーション 3)の逆関数を求めていきます。

その前に

　$^3x$を求める前に、まず参考に$^2x$を求めます。これは、$W(x)$を ランベルトのw関数 として
$x^x=y$
$e^{x\ln(x)}=y$
$x\ln(x)=\ln(x)e^{\ln(x)}=y$
$W(\ln(x)e^{\ln(x)})=\ln(x)=W(\ln(y))$
$x=e^{W(\ln(y))}=\frac{\ln(y)}{W(\ln(y))} $
となります。また、$W(x)$は ラグランジュ反転定理 を使えば求められます。

本題

　それでは$^3x$を求めていきます。$^2x$の時と同じように求めると
$^3x=y$
$(\ln(x))e^{x\ln(x)}=(\ln(x))e^{(\ln(x))e^{\ln(x)}}=\ln(y)$
となります。そのため、$f(x)=xe^{xe^{x}}$として$f^{-1}(x)$分かれば良いと分かります。これも$f'(0)=((0+1)0e^{0}+1)e^{0e^0}=1\neq 0 $なので$W(x)$とおなじように ラグランジュ反転定理 で
$$f^{-1}(x)={\sum_{k=1}^{∞} \frac{(x-f(0))^k}{k!} \lim_{t \to 0} \frac{d^{k-1} }{dt^{k-1}}[(\frac{t}{f(t)-f(0)})^k] }= \sum_{k=1}^{∞} \frac{x^k}{k!} \lim_{t \to 0} \frac{d^{k-1} }{dt^{k-1}}e^{-kte^t}$$
となります。
　そのため、$ \frac{d^n}{dx^n} e^{\alpha xe^x}$を求めれば良いと分かります。これは、 ファー・ディ・ブルーノの公式 より、
$$\frac{d^n}{dx^n} e^{\alpha xe^x}=e^{\alpha xe^x}B_{n}((\alpha xe^x)',(\alpha xe^x)'', \cdots ,(\alpha xe^x)^{(n)})$$
で$\alpha xe^x$のn回微分は$\alpha (x+n)e^x$なので最終的に解をまとめると、
$^3x=y \Longleftrightarrow x( =\sqrt[3]{y}_{s})=e^{f^{-1}(\ln(y))}$ 　$(f(x)=xe^{xe^{x}})$
$$f^{-1}(x)=\sum_{k=1}^{∞} \frac{x^k}{k!} \lim_{t \to 0}e^{-kte^t}B_{k-1}(-k(t+1)e^t,-k(t+2)e^t,\cdots ,-k(t+k-1)e^t)$$
と分かります。なお、$B_{n}(x_1,\cdots ,x_n)$は、 n次完全ベル多項式 です。
　そして、この式を簡略化すると
$$f^{-1}(x)=\sum_{k=1}^{∞}\frac{x^k}{k!} \sum_{n=1}^{k-1} { k-1 \choose n }(-k)^{n}n^{k-n-1}=x-x^2+ \frac{1}{2}x^3+ \frac{5}{6}x^4- \frac{59}{24}x^5+ \cdots $$
にります。

最後に

　以上で今回の$^3x$の逆関数は終わりです。間違っている部分がありましたらご指摘のほどお願いします。投稿を見てくださりありがとうございました。