【Physics Lab. 2026】数理・計算物理班の紹介

【Physics Lab. 2026】数理・計算物理班の紹介

こんにちは！Physics Lab. 2026 数理・計算物理班 班長のなべです。
他の班の紹介記事も続々と上がっていますが、今回は私たちの班について紹介します。 名前からして「難しそう」「カタそう」と思われるかもしれませんが、やっていることは「物理をより深く（数学）、より具体的に（計算）理解しよう！」という、とてもシンプルなものです。

数理・計算物理班とは？

一言で言うと、「物理学」と「他の分野」の境界領域を楽しむ班です 。 具体的には、以下の2つのアプローチで物理に迫ります。

1. 数理物理（Mathematical Physics）

物理学と数学の境界領域です 。 物理法則を数学的に厳密に定式化したり、物理で使われる高度な数学（幾何学や関数解析など）そのものを学んだりします。「なんとなく」の理解で終わらせず、数式の背後にある数学的構造を追い求めます。

2. 量子情報（Quantum Information）

近年爆発的に発展している、量子力学と情報理論の融合分野です。 量子コンピュータのアルゴリズムや、量子もつれ（エンタングルメント）の数理、さらには「量子論とは何か？」という基礎論的な問いにもアプローチします。

3. 計算物理（Computational Physics）

物理学と計算機科学（Computer Science）の境界領域です 。 解析的に解けない複雑な物理の問題をシミュレーションで解いたり、あるいは機械学習の手法を物理に応用したりします 。最近は生成AIの発展もあり、プログラミングのハードルが下がっているので、個人的には一番アツい分野だと思っています 。

どんな本を読んでいるの？

ゼミでは、物理の教科書だけでなく、数学書や最先端の専門書も読みます。 今年度のラインナップを紹介します。かなり「攻めた」選書になっています！

【数理物理・基礎物理系】

『多様体の基礎』（松本幸夫）

ゲージ理論や一般相対性理論といった現代物理学を理解するうえで、幾何学はもはや必須の言葉です。本書はそんな幾何学の中の「多様体論」のバイブルです。わかりやすく丁寧な解説が好評です。

『Physics and Mathematics of Quantum Many-Body Systems』（Hal Tasaki）

田崎晴明先生による、量子多体系の数理物理に関する世界的名著です。量子スピン系や相転移の厳密な取り扱いについて、英語の原著でじっくり読み進めています。

『臨時別冊・数理科学 格子模型の数理物理』（南和彦）

可解格子模型（厳密に解ける模型）の入門書です。イジング模型から始まり、ベーテ仮説やヤン・バクスター方程式といった、数理物理ならではの美しい構造を学びます。

【量子情報・基礎論系】

『行列解析から学ぶ量子情報の数理』（日合文雄）

量子情報の基礎を行列解析（Matrix Analysis）の立場から厳密に展開する本です。量子エンタングルメントや量子通信路符号化などを、数学的に妥協なく学びたい人向けの一冊です。

『図式と操作的確率論による量子論』（中平健治）

量子論を「図式（Diagram）」と「操作的確率論」という現代的な視点から再構築する意欲作です。従来のブラケット記法とは全く異なるアプローチで、量子論の構造を直観的かつ論理的に捉え直します。

活動紹介：格子QCDシミュレーションに挑戦！

「本を読むだけじゃつまらない！手を動かしたい！」 ということで、ここでは私が実際に行った「格子QCD（量子色力学）」のシミュレーションを例として紹介します 。

QCD（量子色力学）とは？

原子核を構成する「陽子」や「中性子」、さらにその中にある「クォーク」や「グルーオン」の振る舞いを記述する理論です 。 この理論は非常に難解で、紙とペンだけ（摂動論など）では計算できない領域がたくさんあります。そこで登場するのが計算機シミュレーションです 。

空間を格子（Lattice）に切る

シミュレーションをするために、連続的な時空を離散的な「格子（グリッド）」に分割します 。

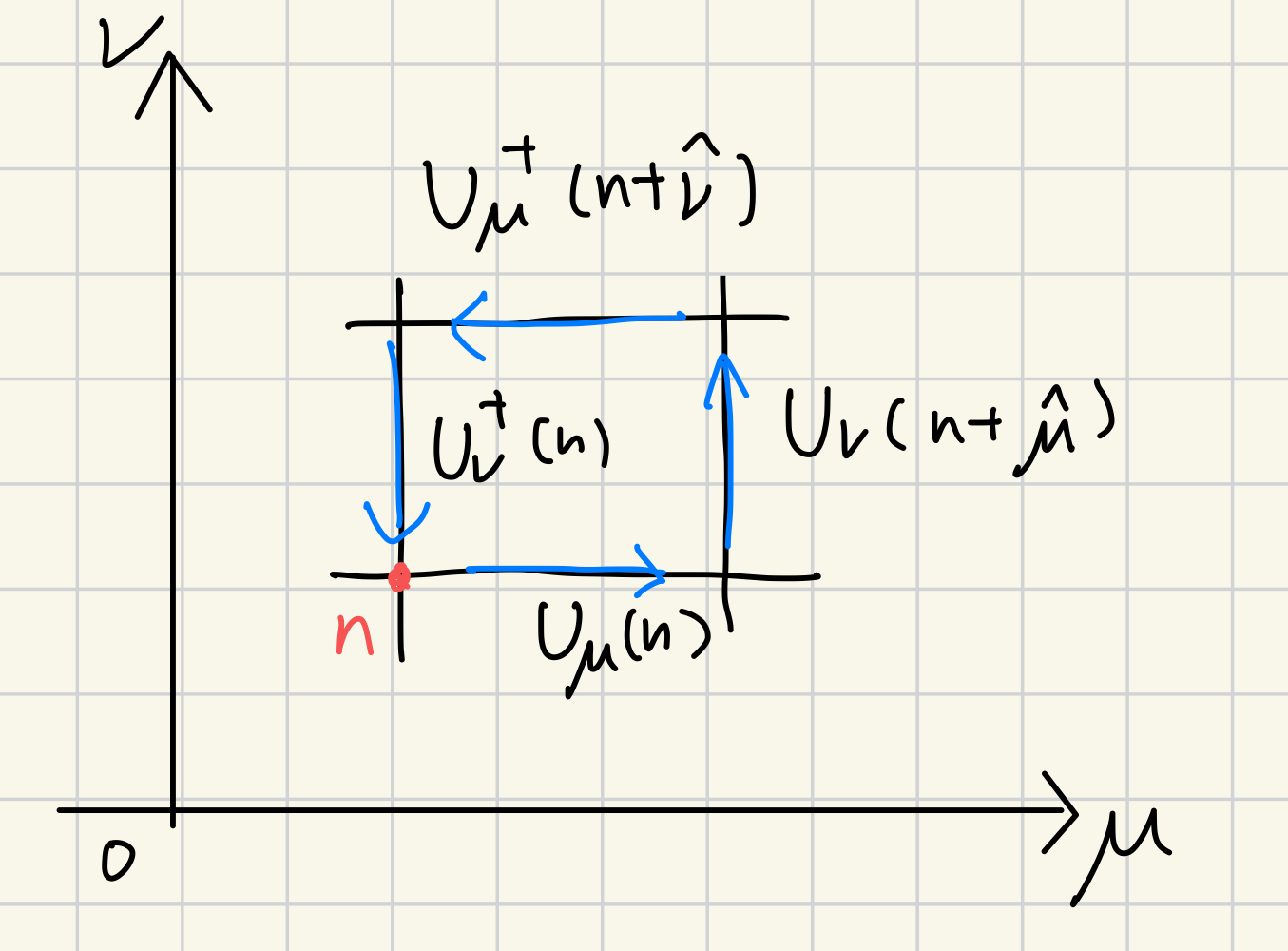プラケットのイメージ図
ここで、時空の各リンク（辺）上に SU(3) 行列$U_\mu​(n)$を配置します。これをリンク変数と呼びます。 そして、格子上の最小のループである「プラケット」$P_{\mu\nu}(n)$ を次のように定義します 。
$ P_{μν}​(n)=U_μ​(n)U_ν(n+\hat{μ})U_μ^\dagger​(n+\hat{ν})U_ν^\dagger​(n)$
これを用いると、ユークリッド時空におけるヤン＝ミルズ理論の作用（ウィルソン作用）は以下のように書けます 。

$S_E^{SU(N_c​)}​[U]=\frac{\beta}{2N_c}​\sum_n ​\sum_\mu \sum_{\nu \neq \mu}\mathrm{Re} \, \mathrm{tr}[1_{N_c​×N_c}​​−P_{μν}​(n)]$

モンテカルロ法で積分する

私たちが知りたい物理量 ⟨O⟩ は、以下の経路積分で与えられます 。

$\langle O \rangle = \frac{1}{Z}\int \mathcal{D}UO[U]e^{-S[U]}$
この積分は変数が多すぎて（自由度が数万〜数億！）、通常の数値積分では不可能です。 そこで、統計力学のアンサンブル平均とみなして、確率的にサンプル（配位）を生成して平均を取る「モンテカルロ法」を使います 。

計算結果：閉じ込め相転移が見えた！

実際にJuliaでクォークの閉じ込め・非閉じ込め相転移をシミュレーションしてみました。 横軸に温度（エネルギースケール $\beta$）、縦軸に「ポリャコフ・ループ（クォークの自由エネルギーに対応する量）」をプロットした結果がこちらです 。
ポリャコフ・ループと結合定数の逆数$\beta$の関係。$\beta \approx 5.7$でポリャコフ・ループが立ち上がっていることが確認できる。

$\beta$がある値を超えたところで、グラフが急激に立ち上がっているのがわかりますか？ ポリャコフ・ループは、クオーク１個の自由エネルギーを$F$としたとき$e^{-F}$と表せます。つまり、グラフが急激に立ち上がることは、自由エネルギー$F$が無限の値(つまりクオーク１個は存在できない)から有限の値(クオーク１個は存在できる)へ変化したことを意味します。これが「相転移（Phase Transition）」です 。 低温では閉じ込められていたクォークが、高温になって「スープ状」に溶け出す様子を、計算機の中で再現できた瞬間です！

最後に

数理・計算物理班では、こうした「理論の深い理解」と「実践的なシミュレーション」の両輪で活動しています。 数理物理で強固な数学力を身につけたい人も、計算物理でゴリゴリ計算して五月祭で発表したい人も、どちらも大歓迎です 。

私たちと一緒に、計算・数理物理強者を目指しましょう！！！