【炎上覚悟】差集合の記法に物申す

$A-B$に物申す

この記法には文句ないのだが...

$A-B$

差集合の記法として減算の記号を用いて$A-B$などと書くことがある。
これには怒り心頭に発する！
その理由を以下に述べていく。
もし可能ならば、読者様にはこれらの理由に対する反論あるいは上回る合理性があればご教授いただきたい。

かの引き算との非合理性

まず譲歩として、差集合の「差」という言葉面を借りて減算の記号を用いたいという気持ちには大いに納得する。
しかし、同じ記号を用いるからにはそれまでの用いられ方と少なからず合理性がなければいけないと考える。
そこで、かの引き算すなわち算数における引き算を引き合いに出す。
$$ 7-3=4 $$
この演算を集合に対応させるのならば以下のようになるのが自然ではないだろうか。
$7>3$に対して順序として包含関係を対応して$A \supset B$
このときは確かに$A-B$は元をいくつか持つ集合であり、$4$に対応させるのは合理的であろう。
しかし、これは本来の差集合より限定的な用い方である。
もちろん、算数を飛び出し負の数も含めて数を拡張することにより、引く数が引かれる数よりも大きい場合にも引き算をすることができる。
$$ 3-7=-4 $$
先ほど同様に対応させると

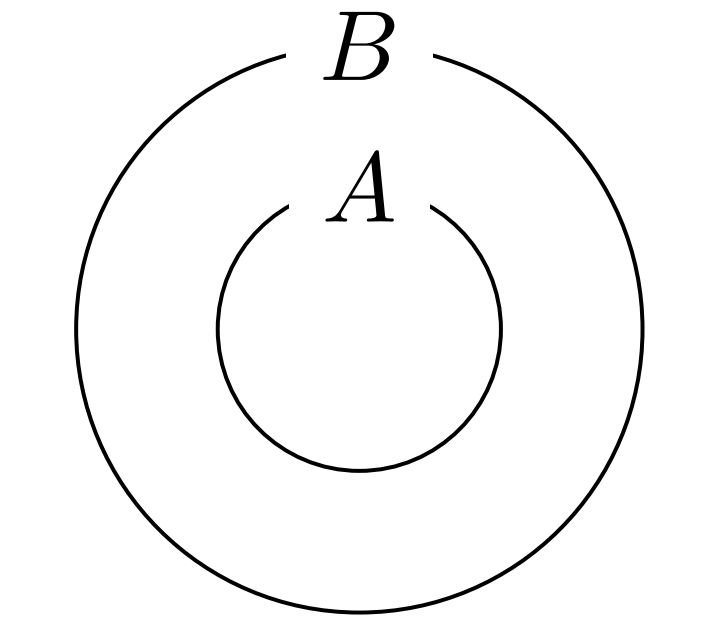
となるが、これはどうだろうか。
$$A-B = \varnothing$$
であり、$\varnothing$は$0$に対応させるべきであるから、$-4$とは対応せず、非合理的である。
さらに、以下のような場合にはどのように対応させようと手も足も出ない。

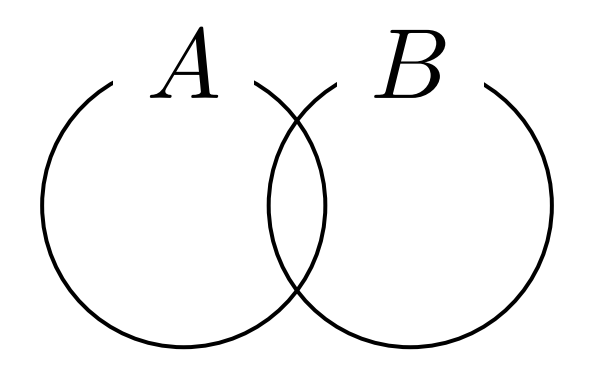
私がこの記法を認めてもよいと思うのは、はじめにあげた場合のみである。
つまり
$$ A-B \coloneqq A \setminus B \enspace (A \supset B) \tag{i} $$
とするべきであるということだ。
かの引き算と自然にアナロジーできるかつ合理的で、納得できる。

和集合と直和

集合の演算においては、差だけでなく和も当然存在した。
こちらはどうだったかを見ておこう。

差集合に減算の記号を用いることを認めるならば、和集合において加算の記号を用いて$A+B$と表記してもよいのではないだろうか。
しかし、この表記は一般的にはすでに異なる意味付けがされている。
$A+B \coloneqq A \cup B \enspace (A \cap B = \varnothing)$
こちらは$A$と$B$が交わらないという条件付きの和集合（直和）なのだ。
それならば！差集合において減算の記号を用いるときに条件付きで定義しておくのが統一的であろう。
よって無条件で$A \setminus B$と同じ意味で用いることは望ましくない。
さらに、$(\mathrm{i})$による定義に納得する理由にもなる。

譲歩

「$A\setminus B$だって右剰余類と見間違えるから良くないだろ！」
確かにその通りだと思います。
しかし、私は$A-B$と書くことを否定しているのであって、$A\setminus B$と書くことを肯定しているわけではありません。
剰余類については割り算の意味合いから合理的に記号が定められているので、(右)剰余類の方に$\setminus$を譲り、差集合についてはまた新たに考え直してもよいかもしれません。