いろんな幾何の問題の個人的解説
はじめに
こんにちは、ぷりんねこです。この記事では題名にもある通りいろんな問題の僕なりの解説を書いていこうと思います。公式解答などと大きく異なるものもけっこうあるので良かったら見ていってください。問題は僕がおもしろいと思ったものを集めてます。では早速いきましょう
.
.
.
平面上に円$C$と$2$点$A,B$があり、$A$は円$C$の内部にあるものとする。$A$を通るが$B$は通らない直線$l$をとり、円$C$との$2$交点を$P,Q$とし、三角形$BPQ$の外心を$O$とする。ある直線$m$が存在し、$l$のとり方によらず$O$は$m$上にあることを示せ
解説
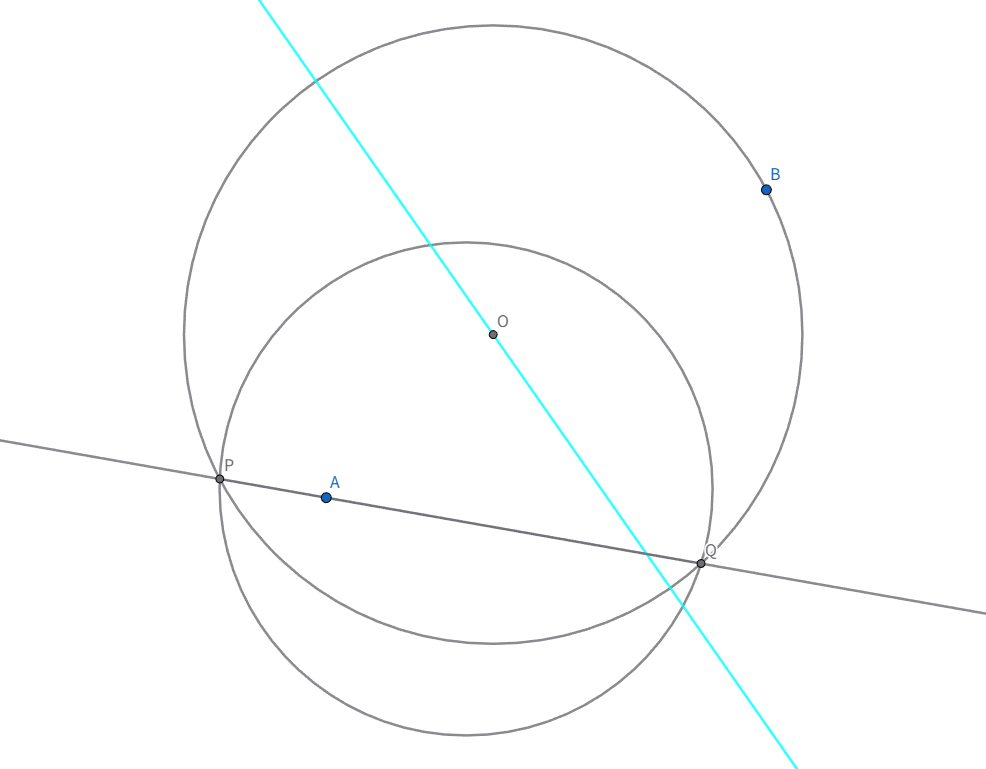
こういう「ある〇〇が存在して~~であることを示せ」系の問題は〇〇の部分が実際にはなんであるか予想したり特定したりすることが大切です。図をいじってみると$m$は$AB$と垂直になりそうです。ここで次の補題を考えます
平面上の線分$AB$と$2$点$P,Q$に対して以下が成り立つ
$AP^2-BP^2=AQ^2-BQ^2 \Longleftrightarrow PQ \perp AB$
どうやっても証明できますがベクトルを使うのが一番簡単だと思います。計算するだけなので省略します
さて、この補題があることによって$AO^2-BO^2$の値を考える動機が生まれます。そして、この値は明らかに方べきの値の形をしています! 今$A$は$2$円の根軸上にあるのでそれぞれの円に関する方べきの値が等しく$AO^2-BO^2=$円$C$における方べきの値$=$一定値となるので、$O$は常に$AB$と垂直な直線上にあります!
この補題はけっこう強いと思うので覚えておいて損はないと思います!
図がシンプルな幾何って意外と難しいですよね
.
.
.
鋭角三角形$ABC$があり、辺$BC$の中点を$M$とする。$\angle BAC$の二等分線を$l$とし、三角形$ABC$の外接円の$C$における接線と$l$との交点を$D$とする。$l$上に点$H$を$\angle ABH=90^{\circ}$であるようにとる。三角形$CDH$の外接円と三角形$ABC$の外接円の交点のうち$C$でない方を$P$とおくとき、$\angle CPM=\angle ACB$を示せ
解説
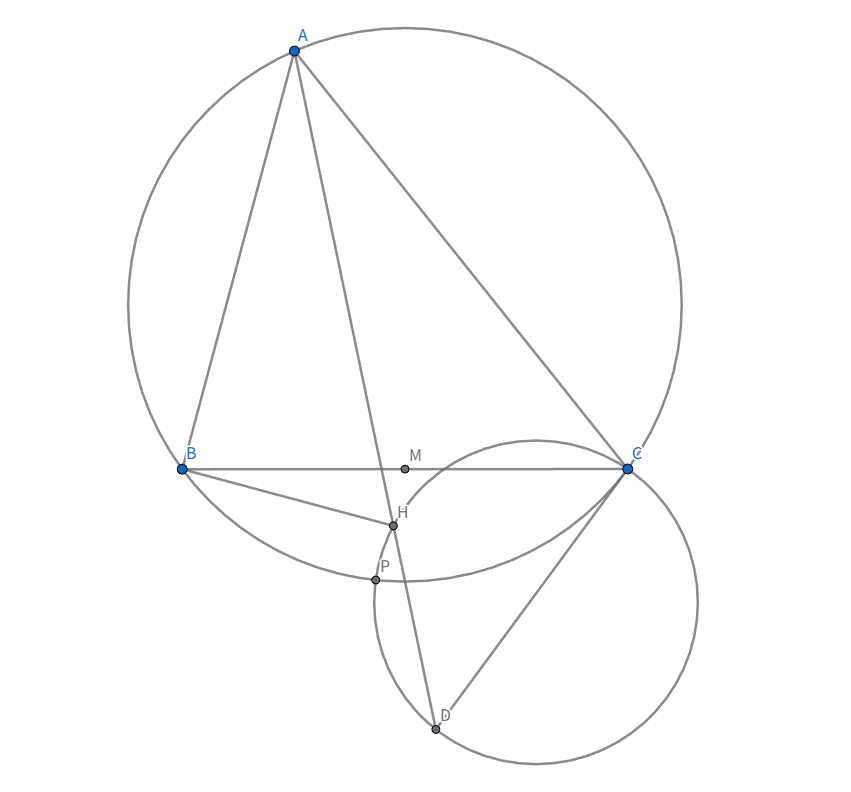
$AP$が三角形$ABC$の$A-symmedian$であることを示せばよいです。三角形$ABC$の$A-symmedian$と外接円の交点を$P$と定義しなおして$4$点$H,P,D,C$の共円を示しましょう。$\angle BAP=\angle MAC$であり、角の二等分線があるので$A$を中心として半径$ \sqrt{AB \cdot AC} $の反転をしたのち$l$に関して対称移動させるという変換を考えます。この変換によって点$X$がうつる先を$X'$と表すことにします。$l$は不変で、$B,C$は互いにうつりあい、三角形$ABC$の外接円は直線$BC$に、$C$における接線は$A,B$を通り$B$で直線$BC$に接する円にうつります。$P'=M,\angle ACH'= 90^{\circ} $であることにも注意するとこの変換をしたあとの図は以下のようになります
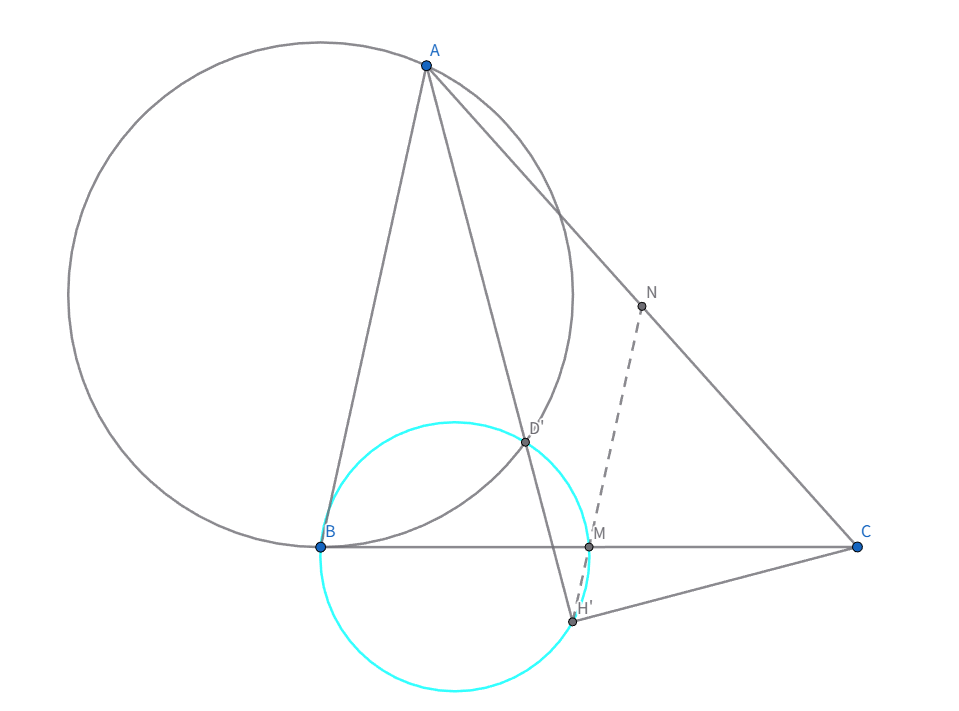
$B,D',M,H'$の共円を示せばいいですね。だいぶ図がすっきりしました。接弦定理から
$\angle D'BM=\angle BAD'=\angle H'AC$なので$\angle D'H'M=\angle H'AC$を示せばよいです。辺$AC$の中点を$N$とすると$N$は三角形$AH'C$の外心なので$\angle NH'A=\angle NAH'=\angle BAH'$より$NH'//AB$であり、$NM//AB$でもあるので$N,M,H'$が共線であることがわかり、示せました!
$A$を中心として半径$ \sqrt{AB \cdot AC} $の反転をしたのち$l$に関して対称移動させるという変換($\sqrt{bc} -inversion$という名前で広く知られている)は反転した後の図で重ね描きを強制的に作っており、非常に強力なものです。よく出てくるのでこちらも覚えておきましょう!
$DA=AB=BC$なる凸四角形$ABCD$があり,$AB$の中点を$M$,$P$を$\angle PCA=\angle PDB=90^{\circ}$となるような点とする。また$O$を中心とする円が$DA,AB,BC$と接している。このとき$M,O,P$の共線を示せ
解説
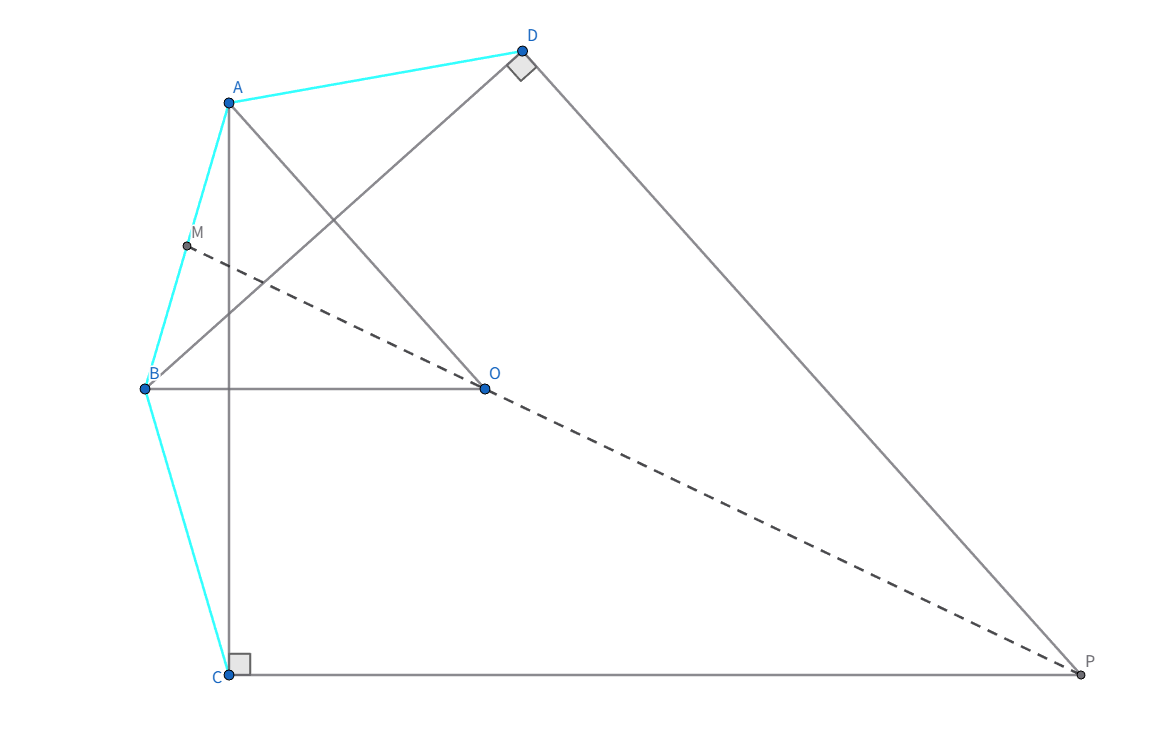
$O$は$\angle ABC,\angle DAB$の二等分線の交点ですね。二等辺三角形があるので$AO,BO$は単に$BD,AC$の垂直二等分線であることが分かります。$△ABO$を基準として考えると$C,D$はそれぞれ$A,B$の対辺に関する対称点で$P$は$CP//BO,DP//AO$となるような点とわかります。$M$が扱いづらいので平行四辺形を作ることを考えます。$AYBO$が平行四辺形となるような$Y$をとります。今$△ABO\equiv △BAY\equiv △ADO\equiv △CBO$(頂点の順番は気にしないでください)ですが$△ADO,△CBO$は$△BAY$と向き(?)が違っていて$△BAY$だけが浮いてしまっているので$ABOX,ABZO$が平行四辺形となるような$X,Z$もとってあげましょう
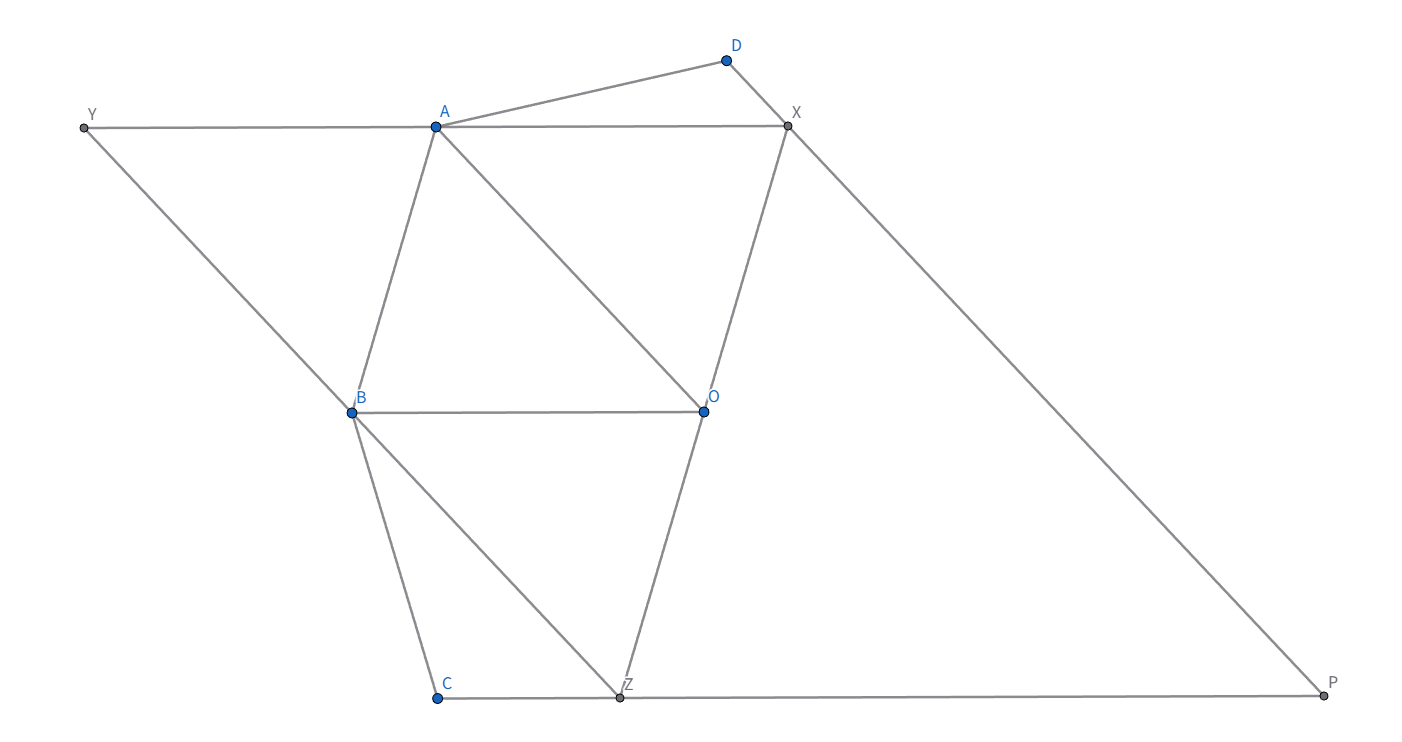
すると$ADXO,BCZO$の等脚台形から$D,X,P$や$C,Z,P$は共線で、$XYZP$が大きな平行四辺形となり$O$は$XZ$の中点なので$Y,O,P$の共線が従い、$M,O,P$の共線が示せました!
中点をみたら平行四辺形を作るのはよくやる手法です。$O$は$△ABP$の重心だったんですね~
おわりに
最後まで読んでいただきありがとうございます。
まだまだ問題は増やしていくつもりです。幾何っていいですね~
