自己紹介＆とある有名問題の証明
はじめまして,katsuo_templeといいます.最初に軽く自己紹介をしておきます.
･高校二年生
･初等幾何が大好き
･OMC青
･乃木坂46のファン
軽く自己紹介をしたところで，本題に移ろうと思います.今回はある幾何の有名問題の自分なりの証明を書こうと思います.拙い部分もあると思いますが，最後まで見てもらえると嬉しいです.
本編
まず初めに以下の補題を示します.
三角形$ABC$の内心を$I$とし，$\angle B,C$の二等分線と対辺の交点をそれぞれ$E,F$とする.円$ABC$と$EF$の交点を$P,Q$とし，$\angle B,C$内の傍心をそれぞれ$I_B,I_C$とする.このとき，五点$I,P,Q,I_B,I_C$は同一円周上にある.
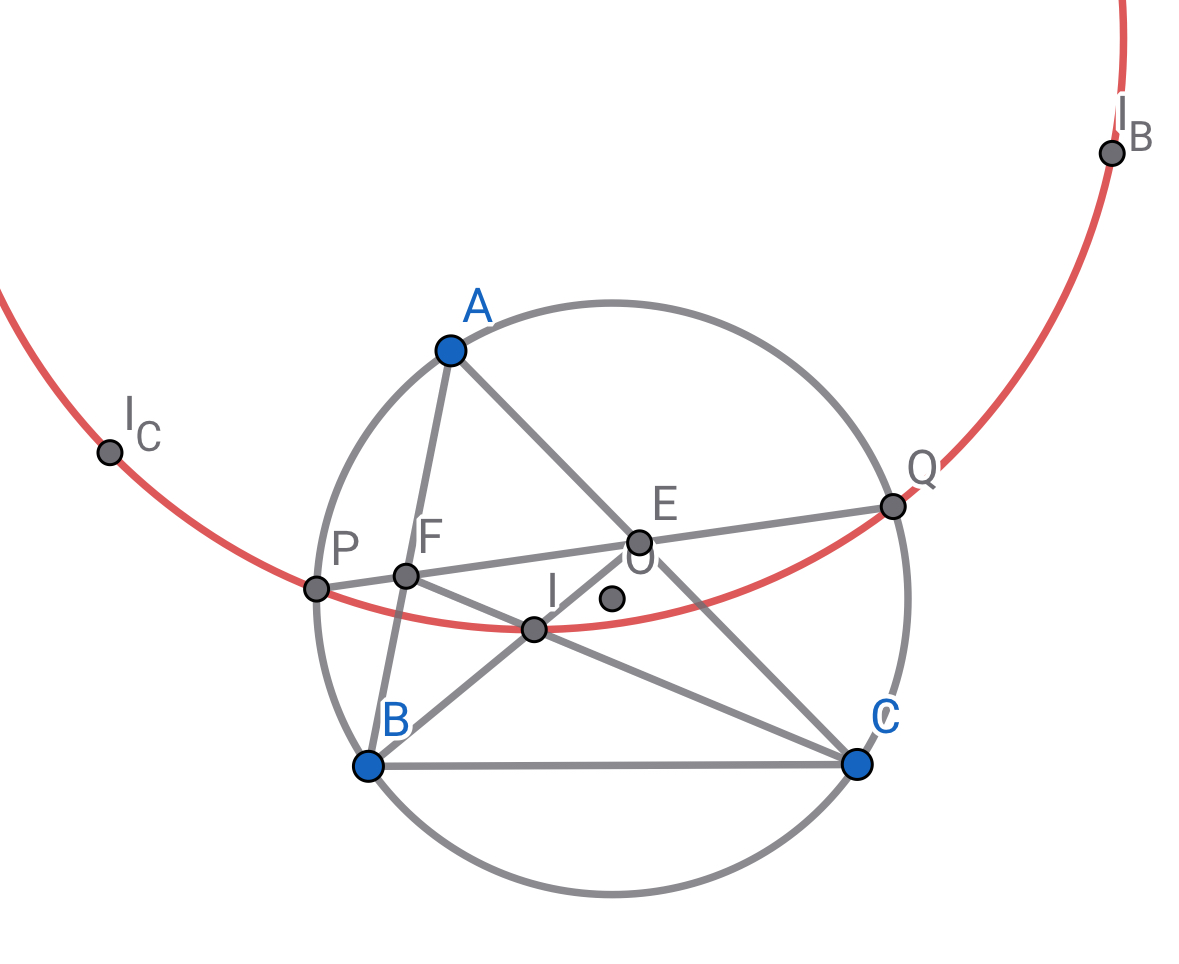補題
四点$A,I,B,I_C$は同一円周上にあるので方べきの定理より$I_CF･IF=AF･BF=PF･QF$が成り立つので四点$P,Q,I,I_C$は同一円周上にある.同様に四点$P,Q,I,I_B$は同一円周上にあるから，五点$I,P,Q,I_B,I_C$は同一円周上にある.
三角形$ABC$において，その外心を$O$，$\angle A$内の傍心を$I_A$とし，$\angle B,C$の二等分線と対辺の交点をそれぞれ$E,F$としたとき，$EF$と$OI_A$は垂直に交わることを示せ.
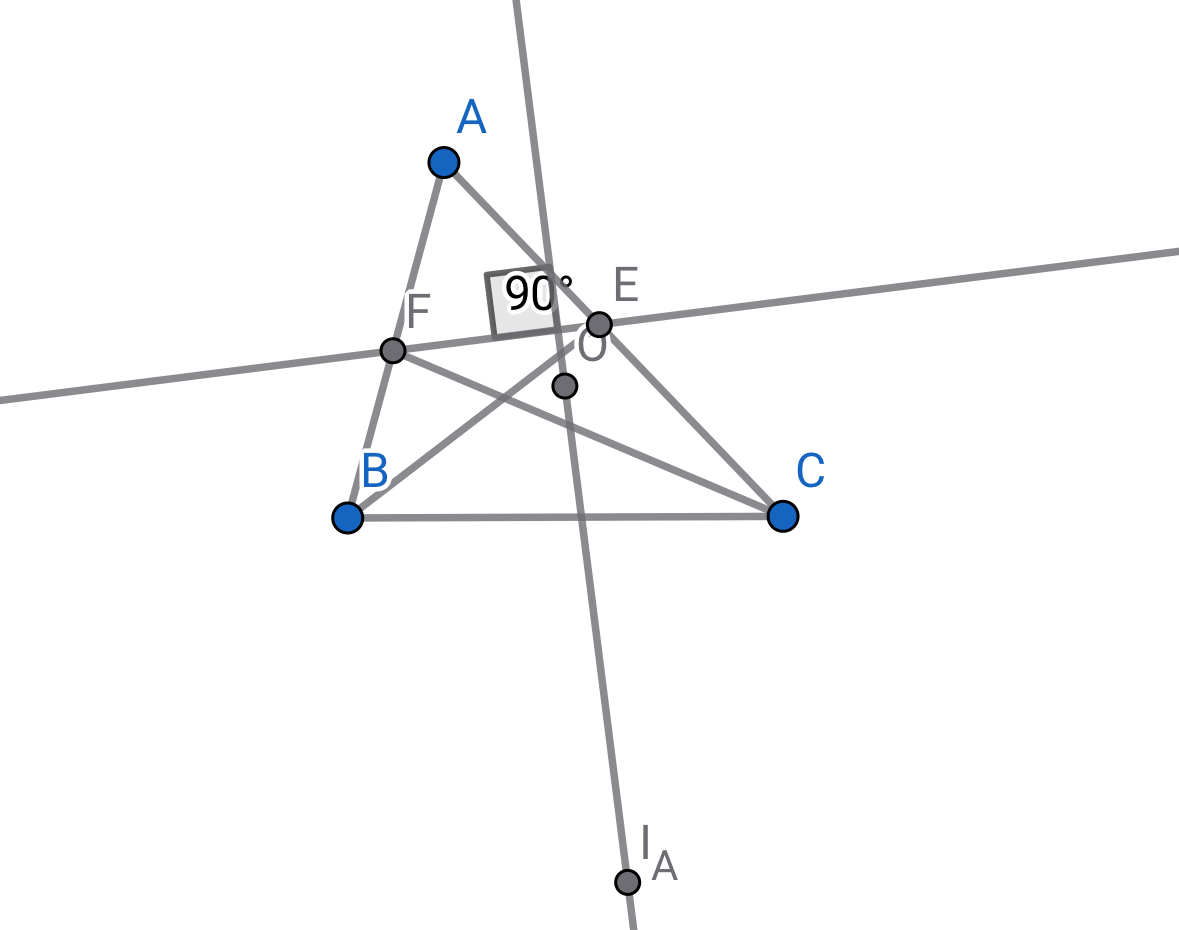有名問題
補題より，$I_A$を中心とする半径$\sqrt{I_AI･I_AA}$の円で反転すると$P,Q$は不変であるので$P,Q$は基準円上にある.したがって，$OI_A$は$PQ$の垂直二等分線であるから,$EF$と$OI_A$は垂直に交わることが示された.
おわりに
いかがだったでしょうか.この問題は多くの証明が存在しますが,この証明方法は自分は見たことがないので，既出だったら教えてほしいです.
この記事を高評価した人
この記事に送られたバッジ
投稿者
