放物線に接する円（中心は軸上）を「二手」で作図する

1. 方法

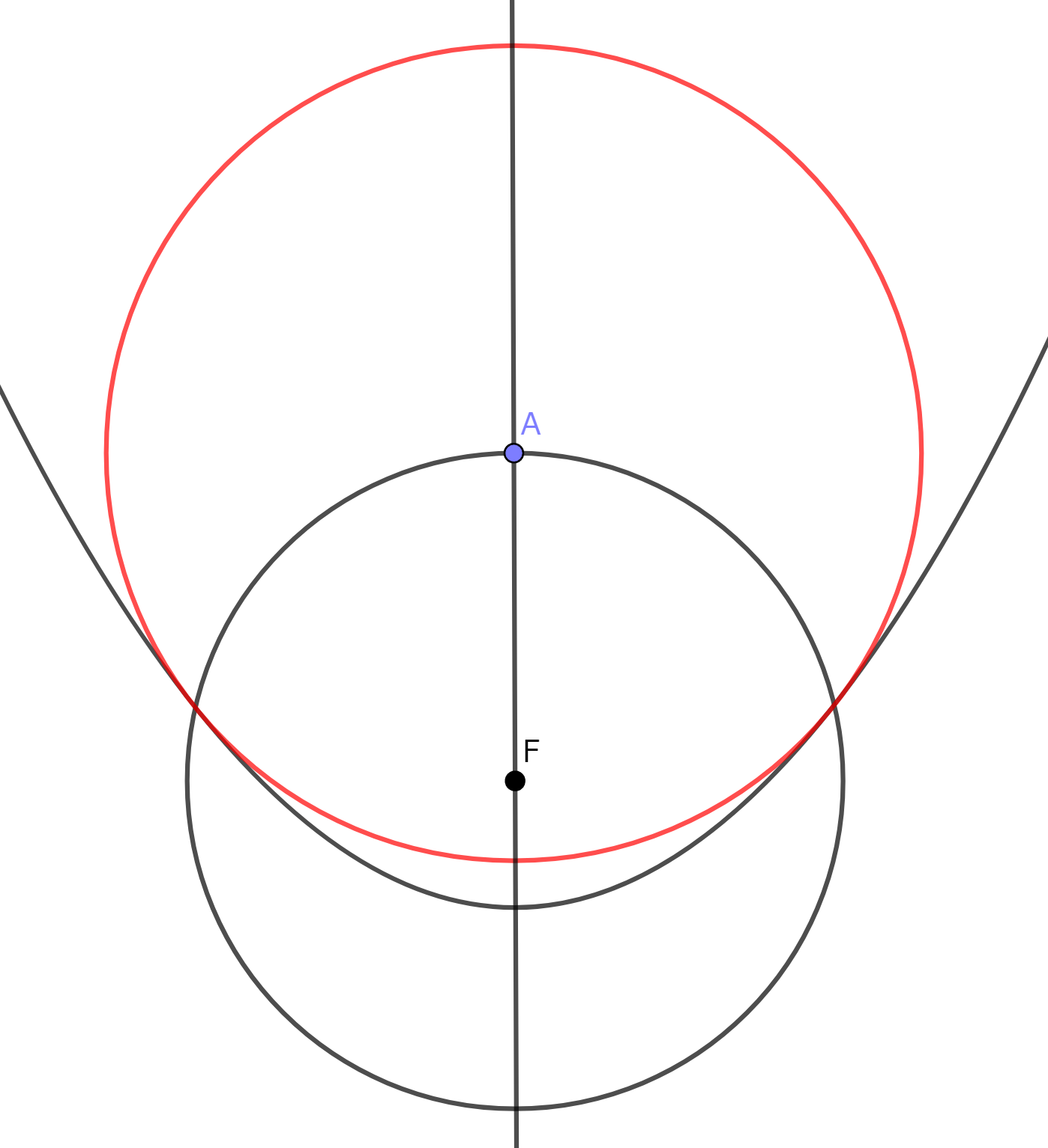
　放物線$P$およびその焦点$\mathrm{F}$、そして軸上の点$\mathrm{A}$が与えられたとき、$\mathrm{A}$を中心として$P$に接する円は、

1. $\mathrm{F}$を中心として、$\mathrm{A}$を通る円$C$を描く
2. $\mathrm{A}$を中心として、放物線$P$と円$C$の交点を通る円$\mathrm{\Gamma}$を描く

の二手で作図できます。

2. 証明

　準線を$l$、$P$と$C$の交点（の片方）を$\mathrm{T}$とします。$\mathrm{T}$から$l$に下ろした垂線の足を$\mathrm{H}$とすると、放物線の定義より$\mathrm{TH}=\mathrm{TF}$です。また、円$C$の定義より$\mathrm{FT}=\mathrm{FA}$です。よって$\mathrm{TH}=\mathrm{FA}$となるので、四角形$\mathrm{ATHF}$は平行四辺形となります。
　四角形$\mathrm{ATHF}$が平行四辺形なので、$\mathrm{AT}\,/\!/\,\mathrm{FH}$です。ここで、$\mathrm{T}$を通り$\mathrm{AT}$に垂直な直線$t$を考えると、$t\perp\mathrm{FH}$であり、放物線の定義より$\mathrm{TH}=\mathrm{TF}$であったので、$t$は線分$\mathrm{FH}$の垂直二等分線です。

　$t$上の$\mathrm{T}$以外の点$\mathrm{T'}$を考えます。$t$は線分$\mathrm{FH}$の垂直二等分線なので$\mathrm{T'F}=\mathrm{T'H}$ですが、$\mathrm{T}'$から準線$l$に下ろした垂線の足を$\mathrm{H'}$とすると$\mathrm{T'H}\neq\mathrm{T'H'}$なので、$\mathrm{T'F}\neq\mathrm{T'H'}$となります。したがって、放物線の定義より、$\mathrm{T}$を除く任意の$\mathrm{T'}$は$P$上にないので、$t$は放物線$P$の$\mathrm{T}$における接線となります（有名な性質です）。
　$t$は円$\mathrm{\Gamma}$の$\mathrm{T}$における接線でもあるので、以上より放物線$P$と円$\mathrm{\Gamma}$が$\mathrm{T}$で接することが示せました。

3. 補足

　放物線$P$と円$C$が共有点を持たない時は、$\mathrm{A}$を中心として$P$に接する円は、自明解である、頂点で接する円しかありません。
　放物線$P$上で焦点$\mathrm{F}$から一番近い点は頂点であり、$P$と$C$が頂点で接する時は、$\mathrm{A}$を中心として$P$に接する円は頂点で接する円のみですが、これは曲率円となります。