和田杯の自分の問題の解説
はじめに
灘校文化祭がありました.自分の問題が3問出たので今回は1問解説します.
猛烈なネタバレなので,まだ考えたいよという人はブラウザバックを
本題
鋭角不等辺三角形$ABC$において,内心を$I$,外心を$O$とする.線分$BC$の垂直二等分線と$\angle{BAC}$の外角二等分線の交点を$P$,三角形$ABC$の内接円と$BC$の接点を$D$とする.三角形$APD$の外接円と直線$BC$の交点を$Q$,直線$PQ$と直線$OI$の交点を$P'$とするとき,$IO:OP'$を求めよ.
まずは以下を補題として与えます.
直線$OI$は,$ABC$の傍心が構成する三角形のオイラー線である.
まず,$I$は傍心三角形の垂心である.(証明略)これは簡単な角度追跡でいえるので,頑張ってみましょう.
そして,$O$は傍心三角形の九点円の中心である.(上が分かれば定義通りですね)
九点円の中心は外心と垂心の中点なので,特に$OI$は傍心三角形のオイラー線である.
ここで,上に書いたことを再度.傍心三角形の外心を$O'$とするとき,$IO=OO'$である.(後で使います)
これは,$AB,AC,BC$それぞれの中点を考えれば分かり易いです.
これも示しておきましょう.
$P$は三角形$ABC$の$B$に関する傍心を$B'$,同様に$C',A'$を定義した時,$B'$と$C'$の中点である.
省略します.一致法で示しましょう.
ここまでわかったので,図を書いたらこんな感じです.
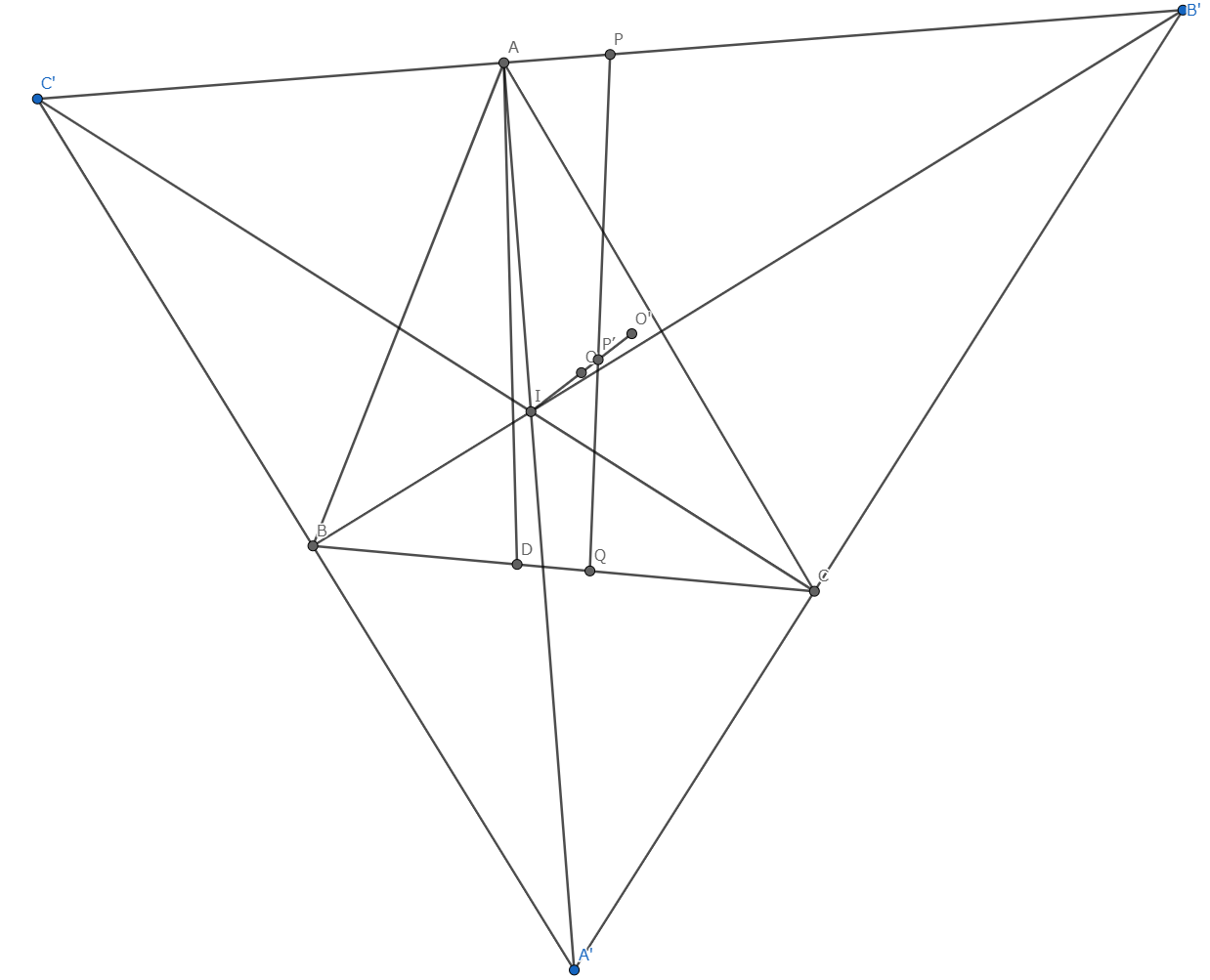
ここからが肝(?)です
$A',Q,P$は共線である.
$A'BC,A'B'C'$は相似であるから,角度追跡より,$BC$の中点を$M$とした時,$AD//A'M$を示せばよい.
まず,不要な点を取っ払って図を書くと,こうです.
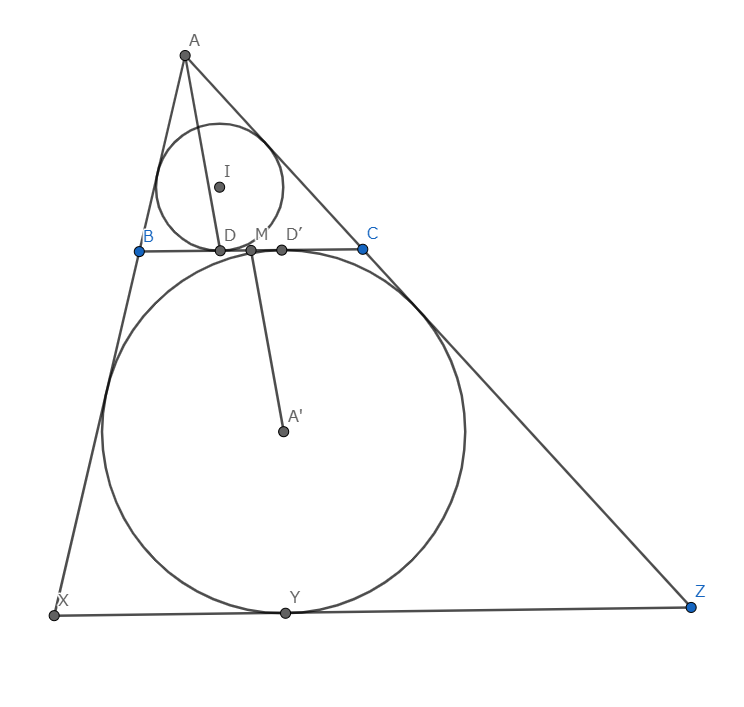
($BC//XZ$であり,傍接円と$Y$で接します.)
$BC//XZ$,$BD:DC=XY:YZ$より,$A,D,Y$は共線である.また,三角形$DD'Y$における中点連結定理より,$AD//A'M$
ここまでくればあと一息です.$P'$は三角形$A'B'C'$の中線とオイラー線の交点であるから,実は三角形$A'B'C'$の重心でした.よって,オイラー線の有名性質より,$IP':P'O'=2:1$であり,上の議論の$IO=OO'$と合わせて,$IO:OP'=\mathbf{3:1}$
おわりに
教育的(笑)な問題になったのではないでしょうか いつか他の2問も書きたいのですが,解説短めの問題のつもりだったのにここに来るまで3回内容飛んで萎えたのでもう嫌です…またいつか気が向けば書くかも知れません
