OMCB034(F) 別解

はじめに

どうも,Weskdohnです。今回はOMCB034(F)の別解を思いついたのでそれについて遊んでいこうと思います(公式解説動画風)。
もしかすると解説と被っているかもしれませんがそれは御愛嬌ということで・・・(追記：ユーザー解説に本記事の内容を移植しました)

問題

OMCB034(F) 問題文
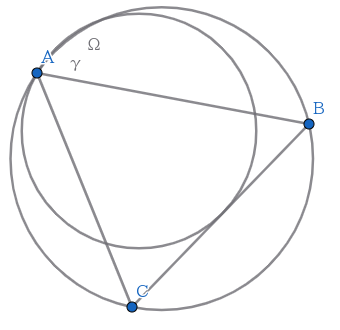イメージ図,厳密じゃないです

解いていく(別解)

まずは正弦定理から,$\dfrac{BC}{sin120°}=242$より$BC=121\sqrt{3}$とわかります．
円γの対処がめんどそうですね・・・内接円じゃないのも余計イライラします()．
どうにか上手い対応を考えましょう．う〜ん・・・・・・せや，相似拡大したれ(唐突)
円γを円Ωに,Aを中心に相似拡大できますね．BC,AC,ABと円γとの交点をD,E,Fとすると，△AFEが△ABCに相似拡大されます．
ここで，△ABCの内接円を考えます．内接円とAB,ACとの接点をP,Qとすると,AP=AQかつ,BP+CQ=BCが成り立ちます．内接円の半径をrとすると，$AP=r・\dfrac{1}{\sqrt{3}}$と書けますね．
よって$AB+BC+CA=242\sqrt{3}+\dfrac{2r}{\sqrt{3}}$と表せます．
ここでAF,AEはそれぞれAB,ACに相似拡大されるのでした．
方べきの定理から,$BD^2=BF・BA,DC^2=CE・CA$です．
$BD=a$とでも置くと,$a^2=\dfrac{100AB}{121}・\dfrac{121AB}{121}$なので$BD=\dfrac{110AB}{121}$,同様に$DC=\dfrac{110AC}{121}$です．
BD+DC=BDですから,$AB+AC=121\sqrt{3}・\dfrac{121}{110}=\dfrac{1331\sqrt{3}}{10}$となります．
よって$AB+BC+CA=\dfrac{2541\sqrt{3}}{10}=242\sqrt{3}+\dfrac{2r}{\sqrt{3}}$となり,$r=\dfrac{121\sqrt{3}}{10}・\dfrac{\sqrt{3}}{2}=\dfrac{363}{20}$が得られました．

最後に

多分これが一番シンプルな解法だと思います。以上,Weskdohnからでした。またね。