2
中学数学解説
Stewartの定理の覚え方
310
0
$$$$
Stewartの定理とは次のような初等幾何の定理である:
(Stewartの定理)
三角形$ABC$の辺$BC$上に点$M$を取り,$a=BC,\;b=AC,\;c=AB,\;d=AM,\;m=BM,\;n=CM$と定めると
$$
b^2m+c^2n=a(d^2+mn)
$$
が成り立つ.
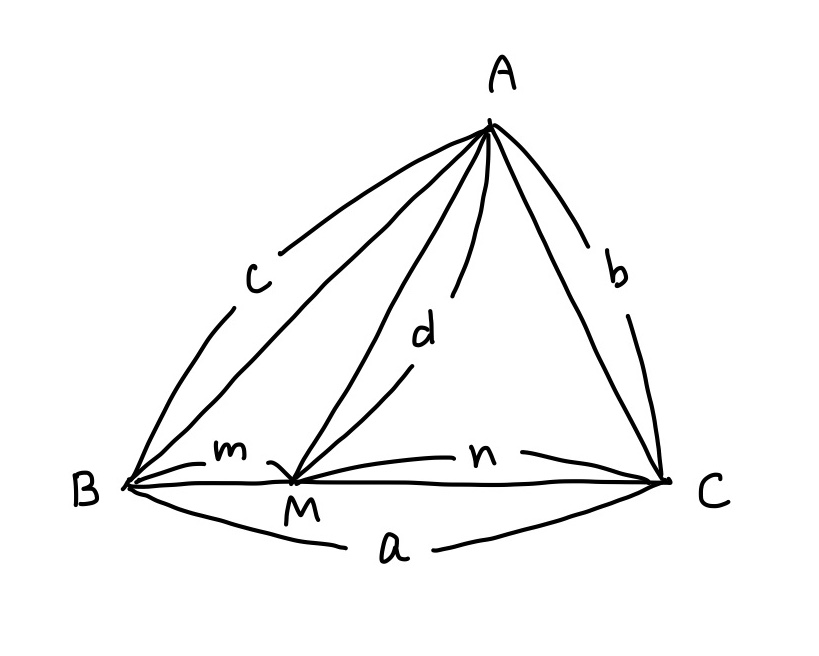 Stewartの定理
Stewartの定理
これがよく考えたら簡単だったという話をしたい(幾何が得意な人にとっては常識かもしれないが・・・).
まず$a=m+n$に注意すると,定理の主張は
$$
b^2\cdot\dfrac{m}{m+n} + c^2\cdot \dfrac{n}{m+n} = d^2+mn
$$
と言い換えられる.さらに辺$BC$上の点$P$に対して
$$
f(P)=AP^2+BP\cdot CP
$$
と定めると,定理の主張は
$$
f(C)\cdot\dfrac{m}{m+n} + f(B)\cdot\dfrac{n}{m+n} = f(M)
$$
と言い換えられる.つまりSwewartの定理は,$f(P)$が辺$BC$上で$1$次関数に従って変化することを表している.
こう捉えると証明も簡単である.
$A(0,h),\;B(p,0),\;C(q,0)$としてよい.辺$BC$上の点$P(x,0)$に対して
$$
f(P)=x^2+h^2+(x-p)(q-x)
$$
となる.これは$x$の$1$次関数なのでよい.
投稿日:2024年10月25日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
J_Koizumi
163
18437
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中