２次式に関する面白い性質

はじめに

次の2問を考えてみてください

｜

｜

｜

ネ

タ

バ

レ

防

止

用

｜

｜

｜
　$a_n=n^2+n+1$とし、$a_n$の最大の素因数を$p_n$とします．
　色々実験していくと
$$n^4+n^2+1=(n^2+1)^2-n^2=(n^2-n+1)(n^2+n+1)=((n-1)^2+(n-1)+1)(n^2+n+1)$$
　すなわち$a_{n^2}=a_{n-1}a_n$が成り立つことが分かります．

　この等式だけ見てもよくわかりませんが、最大の素因数について聞かれてるのでとりあえず両辺の最大の素因数を見てみると$p_{n^2}=\max(p_{n-1},p_n)$となります．

　ところで示したいことは$p_{n^2}=p_{(n+1)^2}$すなわち$\max{(p_{n-1},p_n)}=\max{(p_n,p_{n+1})}$なので、$p_{n-1}\leq p_n\geq p_{n+1}$であったら嬉しいですね

　実はこれはほぼ示せていて、$p_{n^2}=\max(p_{n-1},p_n)$がどういうことを言っているかというと、以下のように横軸$n$、縦軸$p_n$のグラフを考えたときに、（$p_{n-1}$と$p_n$の最大値）が$p_{n^2}$に一致するので

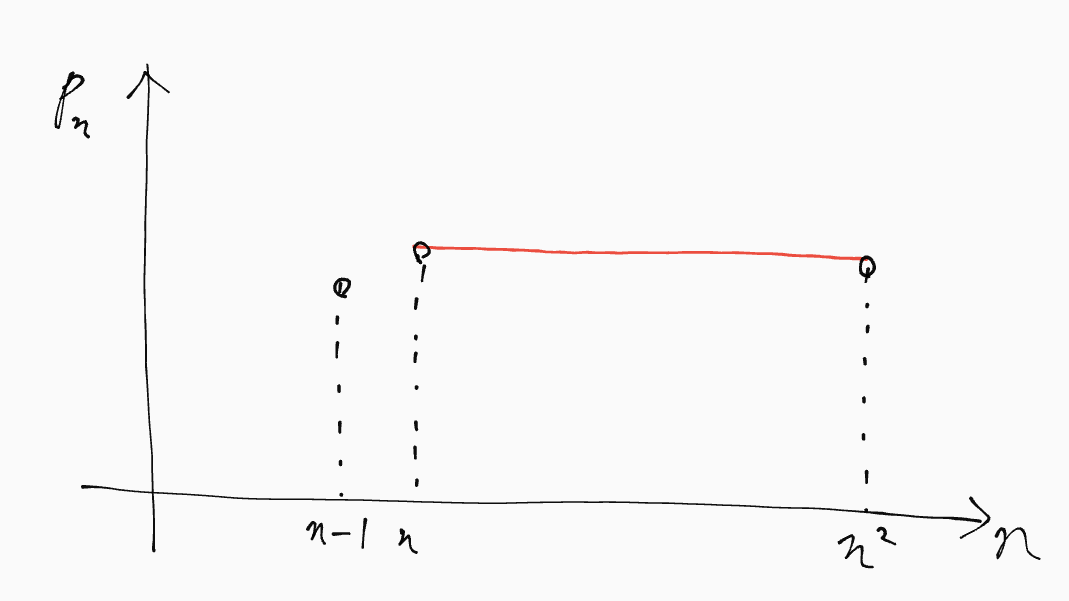
　その間には「上がって下がる」箇所が存在します
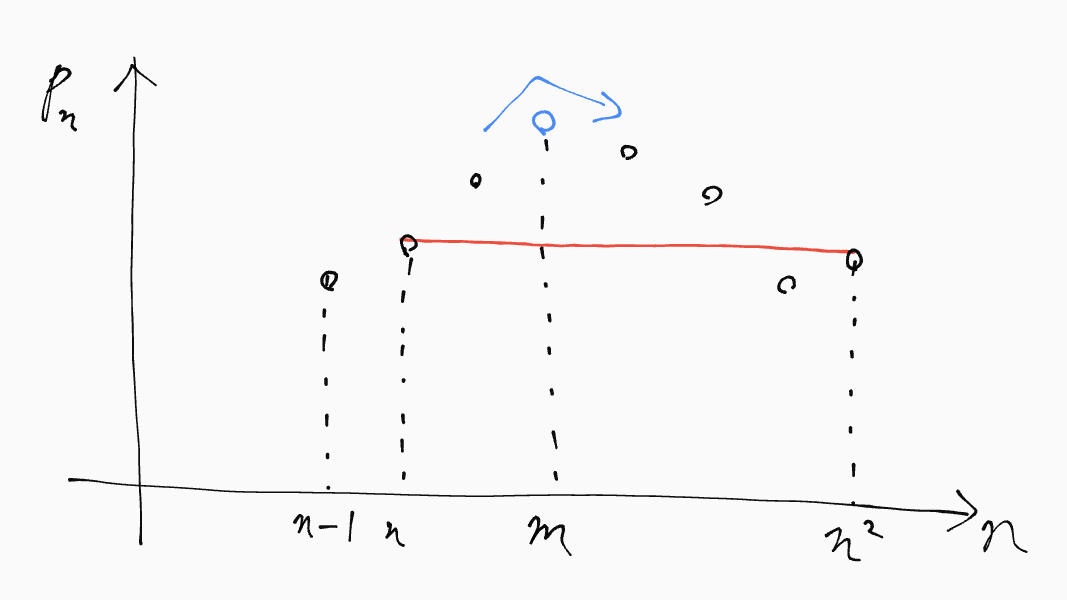離散的なロルの定理 みたいな

　これは$p_{m-1}\leq p_m\geq p_{m+1}$そのものであり、また$n$を十分大きく取ればこのような$m$が十分先でも存在することが示せます．

(実は細かいところに目をつぶっていて、例えば$p_n〜p_{n^2}$が下に凸みたいなグラフだとこのような箇所は存在しないんですが、そのときは$n〜n^2$の間の適当な$m$を取ってきて新しく$p_m〜p_{m^2}$を見てみると$p_{n^2}$ですでに「上がって」いるのでいつか「下がり始める」箇所が存在しますね)

｜

｜

｜

ネ

タ

バ

レ

防

止

用

｜

｜

｜

　$a_n=n^2+1$とします．
　さっきの問題って$a_{n^2}$の$n^2$の部分は別に関係なくて、$a_na_{n+1}=a_{hogehoge}$みたいな形だったらなんでもいいわけですね．

　この問題についても$a_na_{n+1}=a_{hogehoge}$が成り立ってくれないかなぁとかすかな希望をもって計算してみると

$$(n^2+1)((n+1)^2+1)=n^4+2n^3+3n^2+2n+2=(n^2+n+1)^2+1$$
より$a_{n^2+n+1}=a_{n-1}a_n$が成り立ちました．ラッキー

　先程と同様にして$P(n-1)\leq P(n)\geq P(n+1)$なる$n$は無限に存在するので、このような$n$に対して
$$p_{n^2-n+1}=\max(P(n-1),P(n))=P(n),P(n^2+n+1)=\max(P(n),P(n+1))=P(n)$$
　より、$P(n)=P(n^2-n+1)=P(n^2+n+1)$が成り立つから題意が示されました．

一般化

この２つの問題のポイントは

$1$問目は$a_{n-1}a_n=a_{n^2}(a_n=n^2+n+1)$
$2$問目は$a_{n}a_{n+1}=a_{n^2+n+1}(a_n=n^2+1)$

という非自明だけど嬉しい性質が成り立ってくれたことにあります

では、他にも$f(n)f(n+1)=f(hogehoge)$を満たす関数はあるのか？というのが今回の話題です

一般化しすぎると面倒なので今回は$f(n)=n^2+an+b$という関数に限定して考えてみます

$f(n)f(n+1)$を愚直に計算すると

$$\begin{aligned} f(n)f(n+1) &=(n^2+an+b)((n+1)^2+a(n+1)+b)\\ &=(n^2+an+b)(n^2+(a+2)n+a+b+1)\\ &=n^4+2(a+1)n^3+(a^2+3a+2b+1)n^2+(a^2+2ab+a+2b)n+b(a+b+1)\\ &=(n^2+(a+1)n+b)^2+a(n^2+(a+1)n+b)+b\\ &=f(n^2+(a+1)n+b) \end{aligned}$$

なので、実はすべての$2$次式についてそのような$hogehoge$が存在します．かなり意外ですね

$n^2+(a+1)n+b=n+f(n)$なので、以下のようにまとめられます

例題

これを使って問題を解いていきましょう

　とりあえず実験です
$a=3$とすると

$n=5$のとき$5^2+5+3=33=3\times 11$なのでダメ
$n=6$のとき$6^2+6+3=45=3^2\times 5$なのでOK
$n=7$のとき$7^2+7+3=59$なのでダメ
$n=8$のとき$8^2+8+3=75=3\times 5^2$なのでダメ
$n=9$のとき$9^2+9+3=93=3\times 31$なのでダメ

　少なくとも$n^2+n+a$が$n$より大きい素因数を持っていたらダメなんですね．それはそう
　お気持ちとしては$n^2+n+a$を$n$以下の数の積に分解したいという感じです

　じゃあどうすればいいかというと$f(n)f(n+1)=f(n+f(n))$が刺さるわけですね
　さっきの$2$問はこの式を→に見てましたが、←に見ると$f(n+f(n))$という$\mathcal{O}(n^4)$の数が$f(n)$と$f(n+1)$という$\mathcal{O}(n^2)$の数に分解できるということを言っています．　

　実際に代入すると
$$f(n)f(n+1)=f(n^2+2n+a)$$
　なので、$n^2+2n+a=m$とおくと$m$は問題の条件を満たしそうです

　じゃあ本当に満たしているかというと

$f(n)=n^2+n+a\lt m$
$f(n+1)=n^2+3n+a+2\gt m$
　なので$f(n)|m!$ですが$f(n+1)|m!$とは限りません

　ただ$f(n+1)$は$\mathcal{O}(m)$なので、定数倍小さくできさえすれば終わります．具体的には$f(n+1)$が合成数であればいいです

　ここまで来たらどうやっても終わっていて、例えば$n+1=k+f(k)$とでもすれば$f(k)f(k+1)=f(n+1)$なので$f(k),f(k+1),f(n)$はすべて$m$以下でかつ(十分先で)すべて異なるので$f(m)|m!$です

解答

　$m=k^4+4k^3+(2a+3)k^2+2ak+a^2(k\in\mathbb{N})$とすればよい．

あとがき

　JMOにも想定解でこの公式を使った問題がありました

　拡張性はありそうだけど汎用性はなさそうな公式ですが、なんか面白いなーくらいに思ってくれたらいいと思います