算数における円周角の定理とのつきあいかた
算数における円周角の定理とのつきあいかた
東京大学理学部算数学科(理算)に所属している,Sai_baNNtyouと申します.
今日は,算数において円周角の定理やその逆と出会ったときに,どのように接してあげれば良いのか,自分から話しかけに行っても良いのだろうか,そういった悩みを解決します.
中心角と円周角
まずは,中心角や円周角についてまだご存じでない方々のために,中心角と円周角の定義をご紹介します.
円の1つの弧に対して,円の中心からその弧を望む角を,その弧に対する中心角という.また,その弧を除く円周上の1点から弧を望む角を,その弧に対する円周角という.
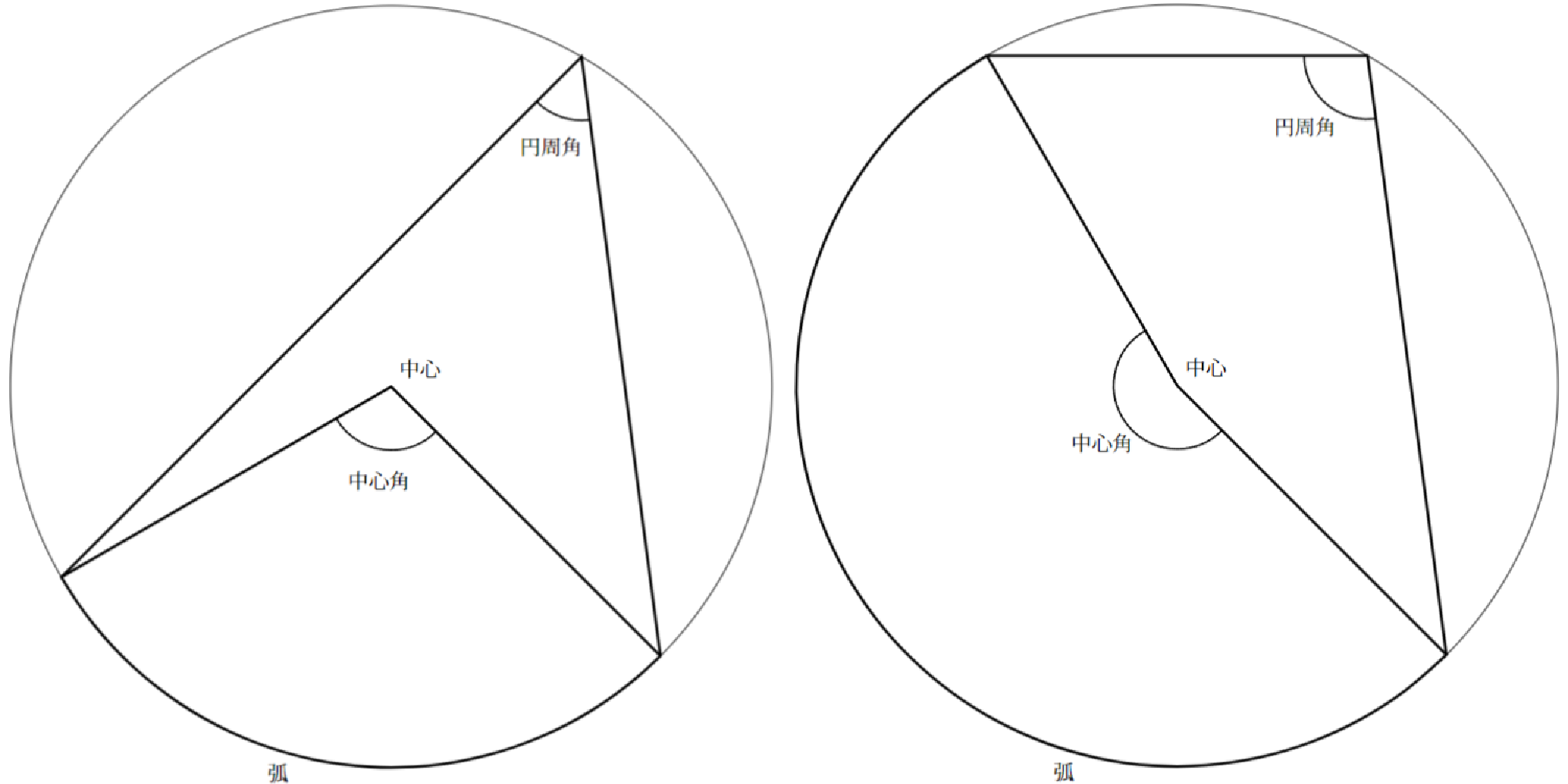 中心角と円周角の定義
中心角と円周角の定義
数学における円周角の定理とその逆
次に,円周角の定理とその逆についてまだご存じでない方々のために,数学における円周角の定理とその逆をご紹介し,証明を与えます.
円の1つの弧に対する中心角の大きさは,その弧に対する円周角の大きさの2倍に一致する.
- 円の中心$O$が円周角$∠APB$の内部にあるとき
直径$PC$をひく.$OA=OP$であるから$∠OPA=∠OAP$.$∠COA$は三角形$OPA$の外角であるから$∠COA=∠OPA+∠OAP=2∠OPA$.同様に$∠COB=2∠OPB$.したがって
$$ \begin{eqnarray} ∠AOB&=&∠COA+∠COB\\ &=&2∠OPA+2∠OPB\\ &=&2∠APB \end{eqnarray} $$
![円の中心!FORMULA[10][37081][0]が円周角!FORMULA[11][510609677][0]の内部にあるとき](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FSFzdFkCpTwnCNyzcJ5uO.png?alt=media) 円の中心$O$が円周角$∠APB$の内部にあるとき
円の中心$O$が円周角$∠APB$の内部にあるとき
- 円の中心$O$が円周角$∠APB$の辺上にあるとき
線分$AP$が円の直径になるとして一般性を欠かない.$OP=OB$であるから$∠OPB=∠OBP$.$∠BOA$は三角形$OPB$の外角であるから$∠BOA=∠OPB+∠OBP=2∠OPB$.したがって$∠AOB=2∠APB$.
![円の中心!FORMULA[21][37081][0]が円周角!FORMULA[22][510609677][0]の辺上にあるとき](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FESrGgQb41jIBF2h3mXhE.png?alt=media) 円の中心$O$が円周角$∠APB$の辺上にあるとき
円の中心$O$が円周角$∠APB$の辺上にあるとき
- 円の中心$O$が円周角$∠APB$の外部にあるとき
点$B$が$∠AOP$の内部にあるとして一般性を欠かない.直径$PC$をひく.$OA=OP$であるから$∠OPA=∠OAP$.$∠COA$は三角形$OPA$の外角であるから$∠COA=∠OPA+∠OAP=2∠OPA$.同様に$∠COB=2∠OPB$.したがって
$$ \begin{eqnarray} ∠AOB&=&∠COB-∠COA\\ &=&2∠OPB-2∠OPA\\ &=&2∠APB \end{eqnarray} $$
![円の中心!FORMULA[35][37081][0]が円周角!FORMULA[36][510609677][0]の外部にあるとき](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FKJOMh9lCiMiBlGNmu9aJ.png?alt=media) 円の中心$O$が円周角$∠APB$の外部にあるとき
円の中心$O$が円周角$∠APB$の外部にあるとき
以上のいずれの場合も$∠AOB=2∠APB$であることが示された.(証明終了)
2円が弦を共有し,その弦に関して2円の中心が互いに異なる側にないとする(一方または両方の円の中心が共有された弦の上にあっても良い).2円のそれぞれに対して,共有された弦に対応する弧を考える.ただし2つの弧は,共有された弦に関して互いに同じ側にあるようにとるものとする.一方の弧に対する中心角の大きさが他方の弧に対する円周角の大きさの2倍に一致するとき,2円は一致する.
円周角の定理により,2つの弧に対する中心角の大きさは一致する.2つの弧に対応する弦は一致していたので,2円の半径の長さは一致する.2円の中心は共有された弦に関して互いに異なる側になかったので,2円は一致する.(証明終了)
算数における円周角の定理
さて,ここからが本題です.
算数において,円周角の定理やその逆が明示的に使われることは多くありません.確かに,これらの定理の状況設定の難しさゆえに,算数において定理として運用していくのは現実的でないでしょう.
しかし円周角の定理に関しては,算数においても事実上使われることがあります.それは,上の良く知られた証明が算数においても理解されやすい手法であり,補助線などを使えば図形の上で直接証明できてしまうからです.
以下では算数における円周角の定理とその証明を与えますが,実際には使用例に示すように証明の手順を辿りながら角の大きさを決定していく使用方法を期待しています.
そのとき必ずしも円を考える必要はないので,円周角の定理の主張を次の等価な主張に変更します.
異なる4点$O$,$A$,$B$,$P$があり,$OA=OB=OP$であるとする.このとき$∠AOB$の大きさは$∠APB$の大きさの2倍に一致する.ただし,$∠AOB$は内部に点$P$を含まない方をとるものとする.
数学における円周角の定理の証明を算数においてもそのまま用いることができる.(証明終了)
算数における円周角の定理の使用例
堅苦しい数学の証明を見ても何も面白くないので,以下の算数の問題で実際に円周角の定理を使ってみましょう.
問題:図のような四角形$ABCD$があり,$AB=BC=CD$,$∠ABC=90^{\circ}$,$∠BCD=60^{\circ}$であるとします.このとき,$∠CAD$の大きさを求めてください.
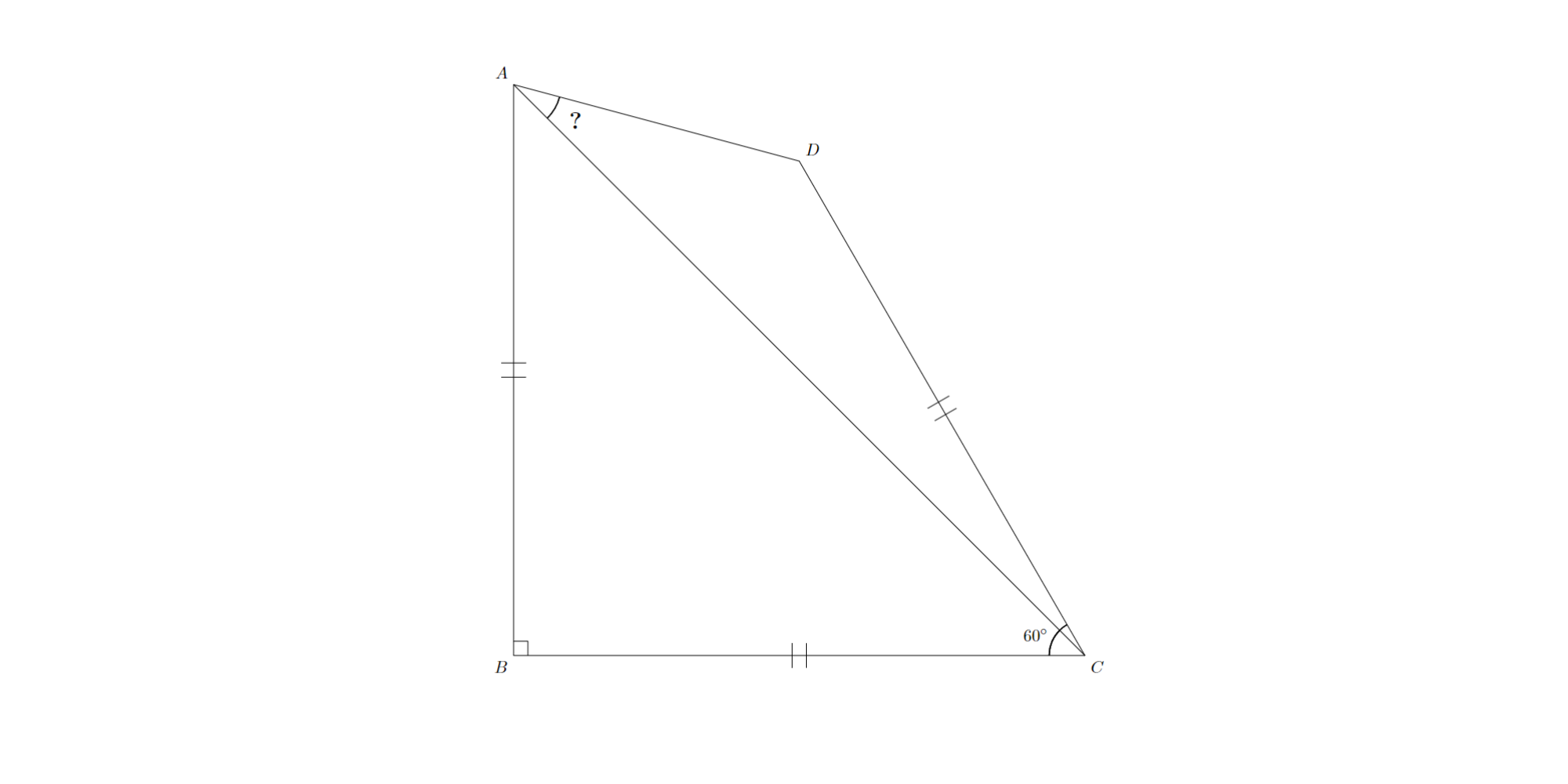 例1 問題
例1 問題
解答解説
図のように線分$BD$をひきます.$BC=CD$と$∠BCD=60^{\circ}$より三角形$BCD$は正三角形であると分かるので,$BD=AB=BC=CD$と$∠DBC=60^{\circ}$が分かります.三角形$ABD$と三角形$ABC$が共に二等辺三角形であることに注意して角の大きさを決定すると,$∠CAD=30^{\circ}$であると分かります.
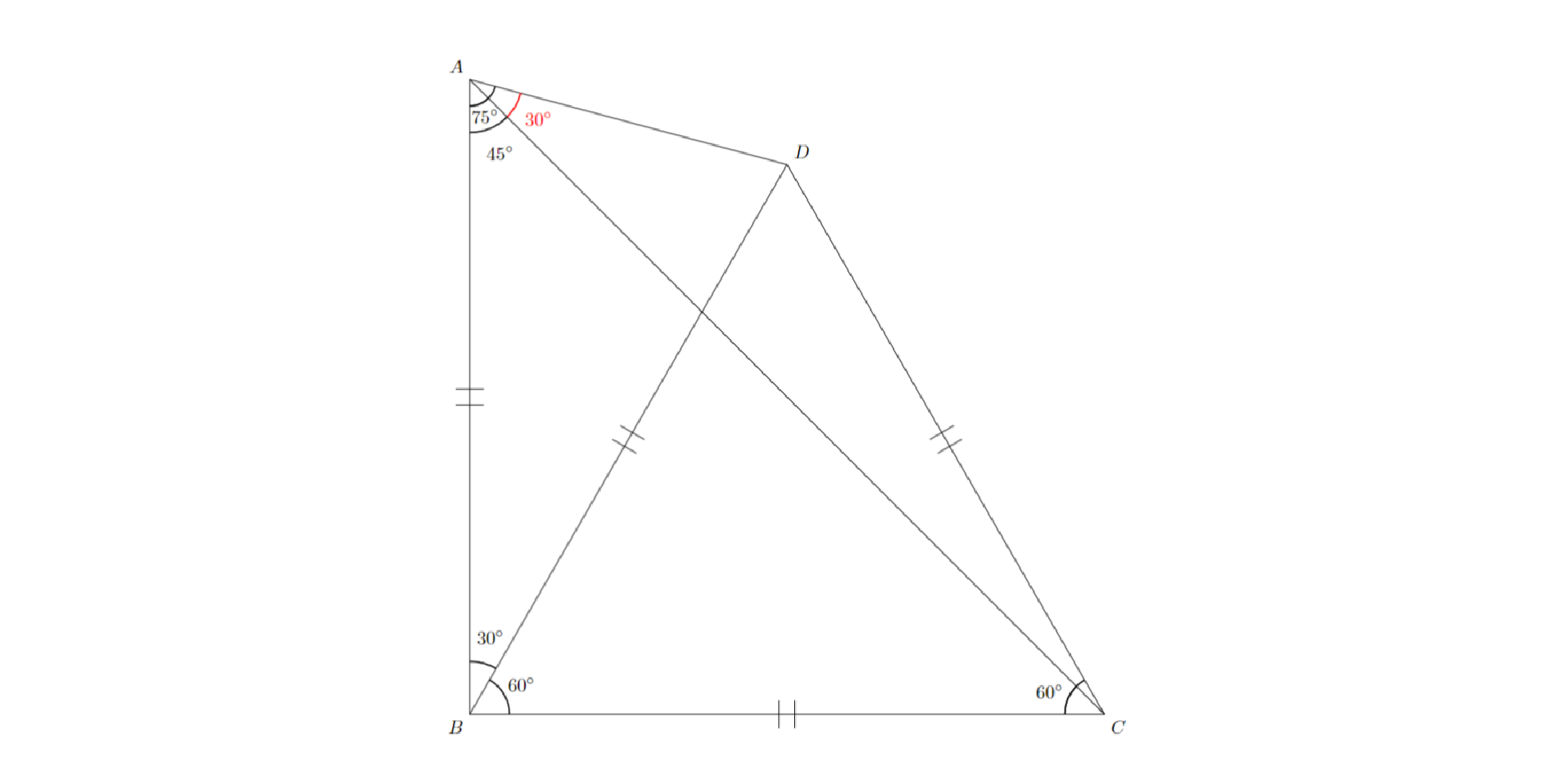 例1 解答解説
例1 解答解説
算数における円周角の定理の逆
さて,ここからが本質です.
算数における円周角の定理は,数学における円周角の定理の主張を算数の言葉に変更するだけで導入され,数学における円周角の定理の証明をそのまま用いて証明されました.一方で円周角の定理の逆を算数に導入するにあたっては,数学における円周角の定理の逆の主張を算数の言葉に変更したうえで,数学における円周角の定理の逆の証明を大きく変更します.
異なる4点$O$,$A$,$B$,$P$があり,$OA=OB$であるとする.$∠AOB$のうち内部に点$P$を含まない方の大きさが,$∠APB$の大きさの2倍に一致するとき,以下のいずれかに該当するならば$OP=OA=OB$となる.
- 線分$AB$に関して点$O$と点$P$が同じ側にあり,$∠APB$が$90^{\circ}$よりも小さい.
- 線分$AB$に関して点$O$と点$P$が異なる側にあり,$∠APB$が$90^{\circ}$よりも大きい.
- 線分$AB$の上に点$O$があり,$∠APB$が$90^{\circ}$に等しい.
円周角の定理の逆の主張の変更点
円周角の定理のときと同様に円を用いた主張をやめ,長さに関する主張に変更しました.このとき,「2円は一致する」という結論をやめ,「長さが等しくなる」という結論に変更しています.これは,異なっていても良いと仮定した2つの図形が実は一致していたという議論の流れが図形の上で表現しにくく,算数においてなじみ深いものでないので,代わりに三角形が二等辺三角形であったというなじみ深い議論の流れに変更したかったからです.
また,算数における円周角の定理の逆では3つの条件を挙げ,そのいずれかに該当していることを適用条件としました.これらの条件は,数学における円周角の定理の逆で「弦に関して2円の中心が互いに異なる側にないとする(一方または両方の円の中心が共有された弦の上にあっても良い)」と表現した条件に対応しています.
算数における円周角の定理の逆の証明の方針
これまで述べてきたように,図形の上で直接証明することを目指し,異なっていても良いとして描いた2つの図形が実は一致していたという議論の流れを用いません.しかし,円周角の大きさが分かっている円の中心角の大きさを円周角の定理から求めて2円の中心角の大きさを比較する方法では,このような議論の流れを避けられません.そこで以下では,円周角の定理の逆の証明に円周角の定理を用いることをやめ,三角形の相似を用いた直接的な証明を与えます.
- 線分$AB$に関して点$O$と点$P$が同じ側にあり,$∠APB$が$90^{\circ}$よりも小さいとき
- 点$O$が$∠APB$の内部にあるとき
直線$PB$に関して点$A$と対称な点$A^{\prime}$をとる.直線$PB$に関する対称性から以下が従う.
$$ \begin{eqnarray} ∠APB=∠A^{\prime}PB (1) PA=PA^{\prime} (2) ∠BAA^{\prime}=∠BA^{\prime}A (3) \end{eqnarray} $$
(1)から以下が従う.
$$ \begin{eqnarray} ∠APA^{\prime}=∠APB+∠A^{\prime}PB=2∠APB=∠AOB (4) \end{eqnarray} $$
(2)と$OA=OB$と(4)より三角形$PAA^{\prime}$と三角形$OAB$とは相似であるから,以下が従う.
$$ \begin{eqnarray} PA:AA^{\prime}=OA:AB (5) ∠PAA^{\prime}=∠OAB (6) \end{eqnarray} $$
(6)から以下が従う.
$$ \begin{eqnarray} ∠BAA^{\prime}=∠OAB-∠OAA^{\prime}=∠PAA^{\prime}-∠OAA^{\prime}=∠OAP (7) \end{eqnarray} $$
(5)と(7)より三角形$BAA^{\prime}$と三角形$OAP$とは相似であるから,以下が従う.
$$ \begin{eqnarray} ∠BA^{\prime}A=∠OPA (8) \end{eqnarray} $$
(3)と(7)と(8)より
$$ \begin{eqnarray} ∠OAP=∠BAA^{\prime}=∠BA^{\prime}A=∠OPA \end{eqnarray} $$
であるから,三角形$OAP$は$OA=OP$の二等辺三角形であると分かり,$OP=OA=OB$を得る.
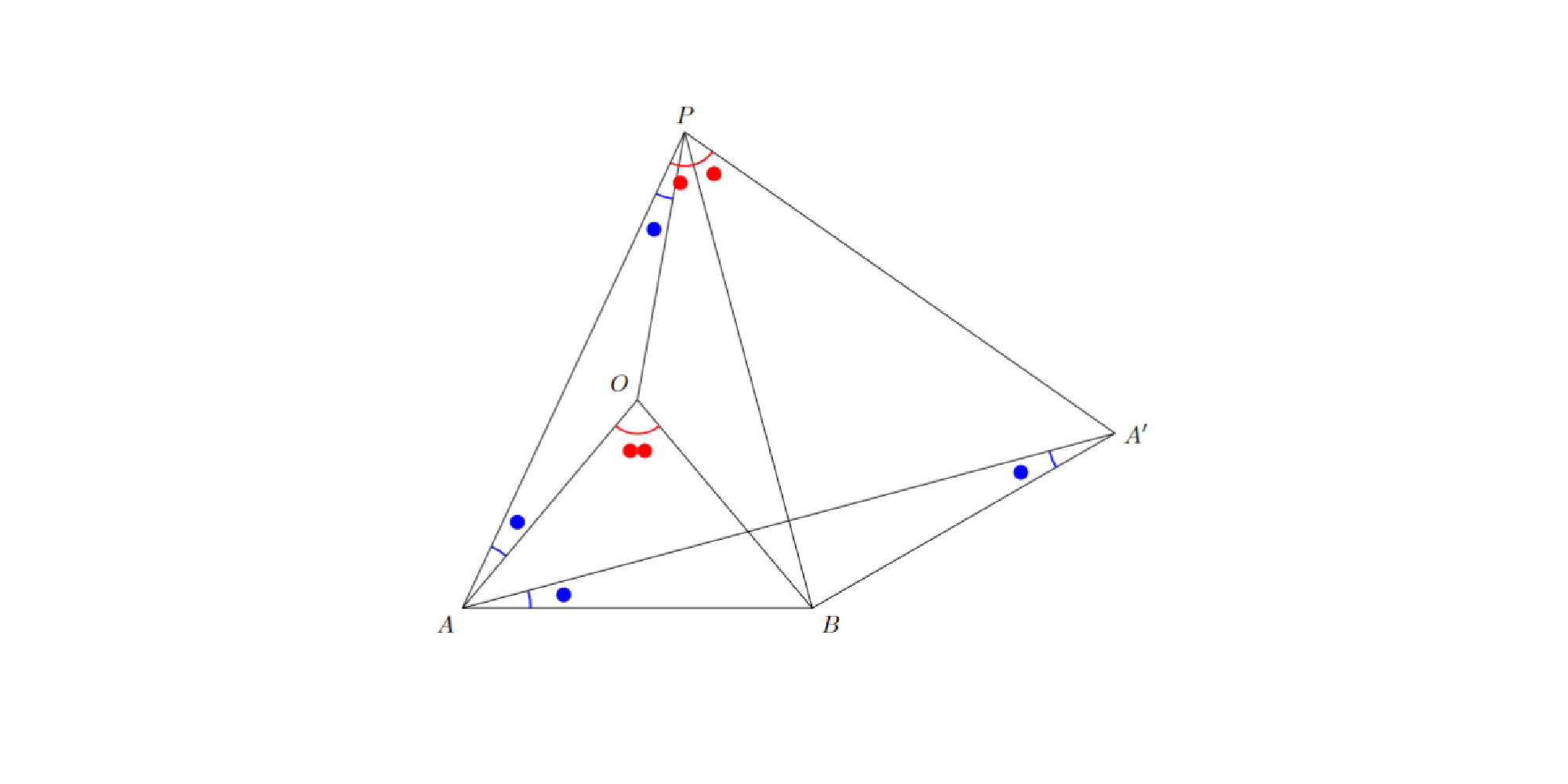 1.i.のとき
1.i.のとき
- 点$O$が$∠APB$の辺上にあるとき
点$O$が線分$AP$上にあるとして一般性を欠かない.$∠BOA$は三角形$OPB$の外角であるから$∠OBP=∠BOA-∠OPB=∠OPB$.よって三角形$OPB$は$OB=OP$の二等辺三角形であると分かり,$OP=OA=OB$を得る.
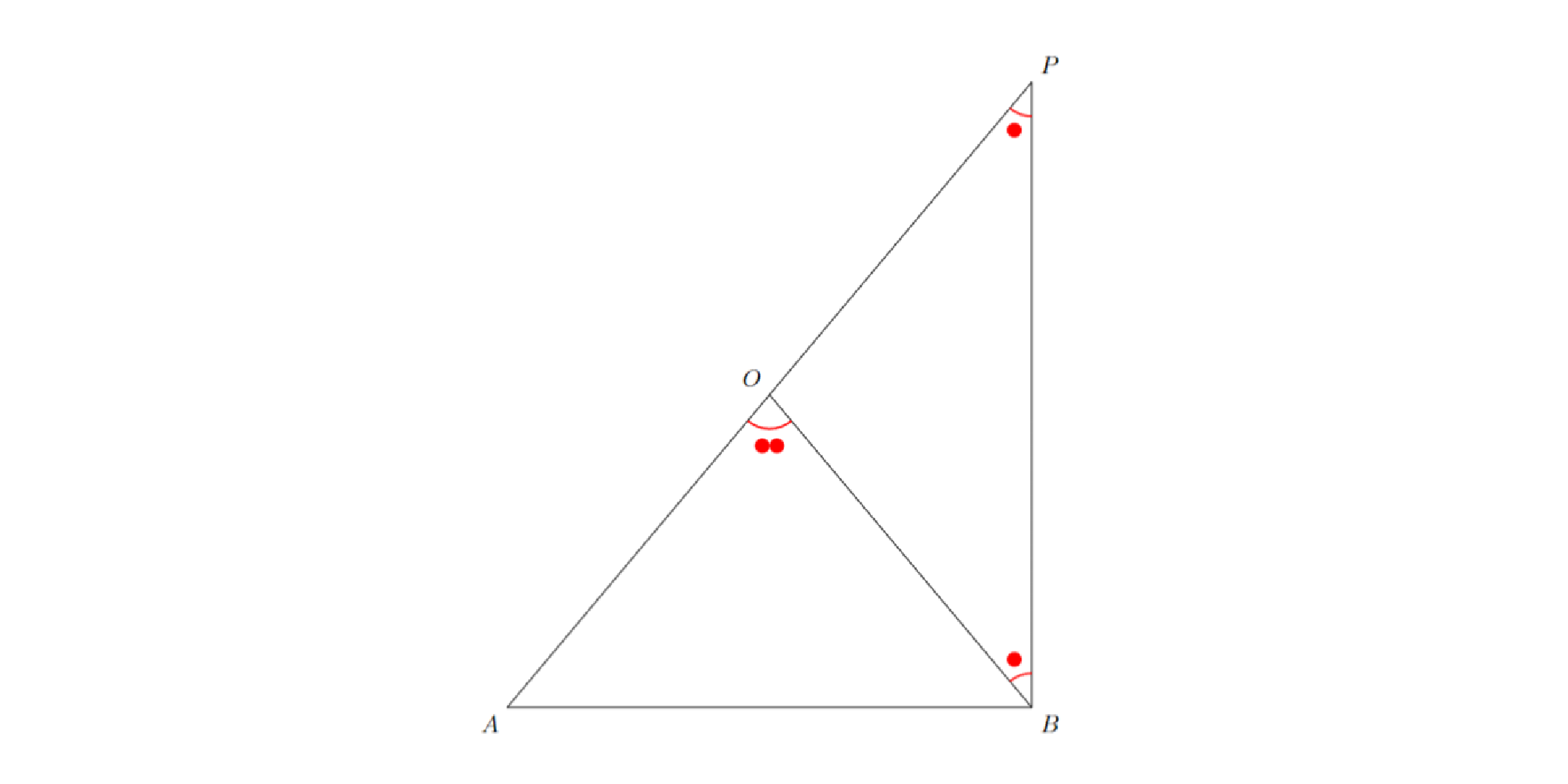 1.ii.のとき
1.ii.のとき
- 点$O$が$∠APB$の外部にあるとき
点$B$が$∠AOP$の内部にあるとして一般性を欠かない.直線$PB$に関して点$A$と対称な点$A^{\prime}$をとる.直線$PB$に関する対称性から以下が従う.
$$ \begin{eqnarray} ∠APB=∠A^{\prime}PB (1) PA=PA^{\prime} (2) ∠BAA^{\prime}=∠BA^{\prime}A (3) \end{eqnarray} $$
(1)から以下が従う.
$$ \begin{eqnarray} ∠APA^{\prime}=∠APB+∠A^{\prime}PB=2∠APB=∠AOB (4) \end{eqnarray} $$
(2)と$OA=OB$と(4)より三角形$PAA^{\prime}$と三角形$OAB$とは相似であるから,以下が従う.
$$ \begin{eqnarray} PA:AA^{\prime}=OA:AB (5) ∠PAA^{\prime}=∠OAB (6) \end{eqnarray} $$
(6)から以下が従う.
$$ \begin{eqnarray} ∠BAA^{\prime}=∠PAA^{\prime}-∠PAB=∠OAB-∠PAB=∠OAP (7) \end{eqnarray} $$
(5)と(7)より三角形$BAA^{\prime}$と三角形$OAP$とは相似であるから,以下が従う.
$$ \begin{eqnarray} ∠BA^{\prime}A=∠OPA (8) \end{eqnarray} $$
(3)と(7)と(8)より
$$ \begin{eqnarray} ∠OAP=∠BAA^{\prime}=∠BA^{\prime}A=∠OPA \end{eqnarray} $$
であるから,三角形$OAP$は$OA=OP$の二等辺三角形であると分かり,$OP=OA=OB$を得る.
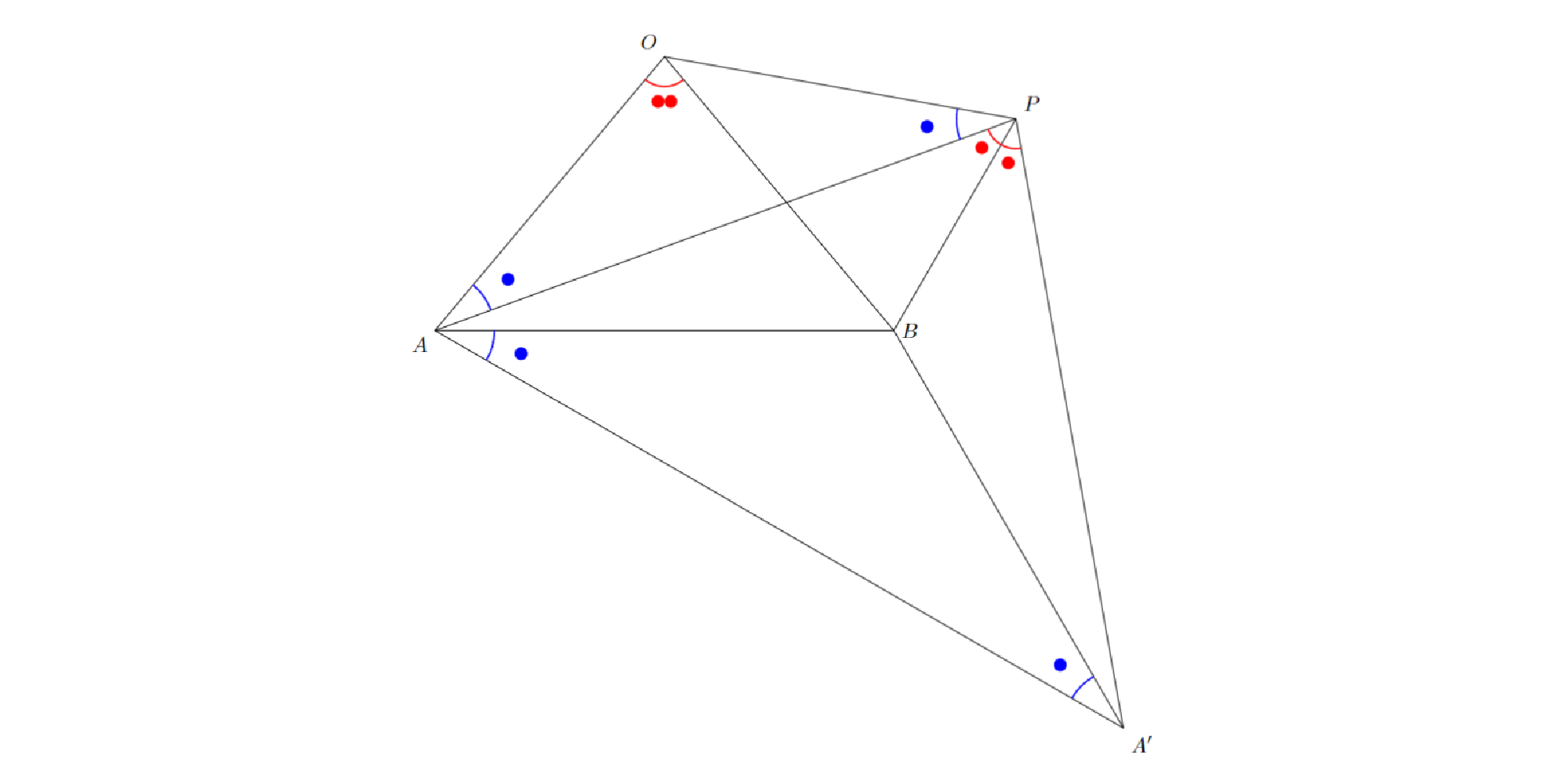 1.iii.のとき
1.iii.のとき
- 点$O$が$∠APB$の内部にあるとき
- 線分$AB$に関して点$O$と点$P$が異なる側にあり,$∠APB$が$90^{\circ}$よりも大きいとき
直線$PB$に関して点$A$と対称な点$A^{\prime}$をとる.直線$PB$に関する対称性から以下が従う.
$$ \begin{eqnarray} ∠APB=∠A^{\prime}PB (1) PA=PA^{\prime} (2) ∠BAA^{\prime}=∠BA^{\prime}A (3) \end{eqnarray} $$
(1)から以下が従う.ただし$∠APA^{\prime}$と$∠AOB$は$180^{\circ}$よりも大きい方をとる.
$$ \begin{eqnarray} ∠APA^{\prime}=∠APB+∠A^{\prime}PB=2∠APB=∠AOB (4) \end{eqnarray} $$
(2)と$OA=OB$と(4)より三角形$PAA^{\prime}$と三角形$OAB$とは相似であるから,以下が従う.
$$ \begin{eqnarray} PA:AA^{\prime}=OA:AB (5) ∠PAA^{\prime}=∠OAB (6) \end{eqnarray} $$
(6)から以下が従う.
$$ \begin{eqnarray} ∠BAA^{\prime}=∠PAA^{\prime}+∠PAB=∠OAB+∠PAB=∠OAP (7) \end{eqnarray} $$
(5)と(7)より三角形$BAA^{\prime}$と三角形$OAP$とは相似であるから,以下が従う.
$$ \begin{eqnarray} ∠BA^{\prime}A=∠OPA (8) \end{eqnarray} $$
(3)と(7)と(8)より
$$ \begin{eqnarray} ∠OAP=∠BAA^{\prime}=∠BA^{\prime}A=∠OPA \end{eqnarray} $$
であるから,三角形$OAP$は$OA=OP$の二等辺三角形であると分かり,$OP=OA=OB$を得る.
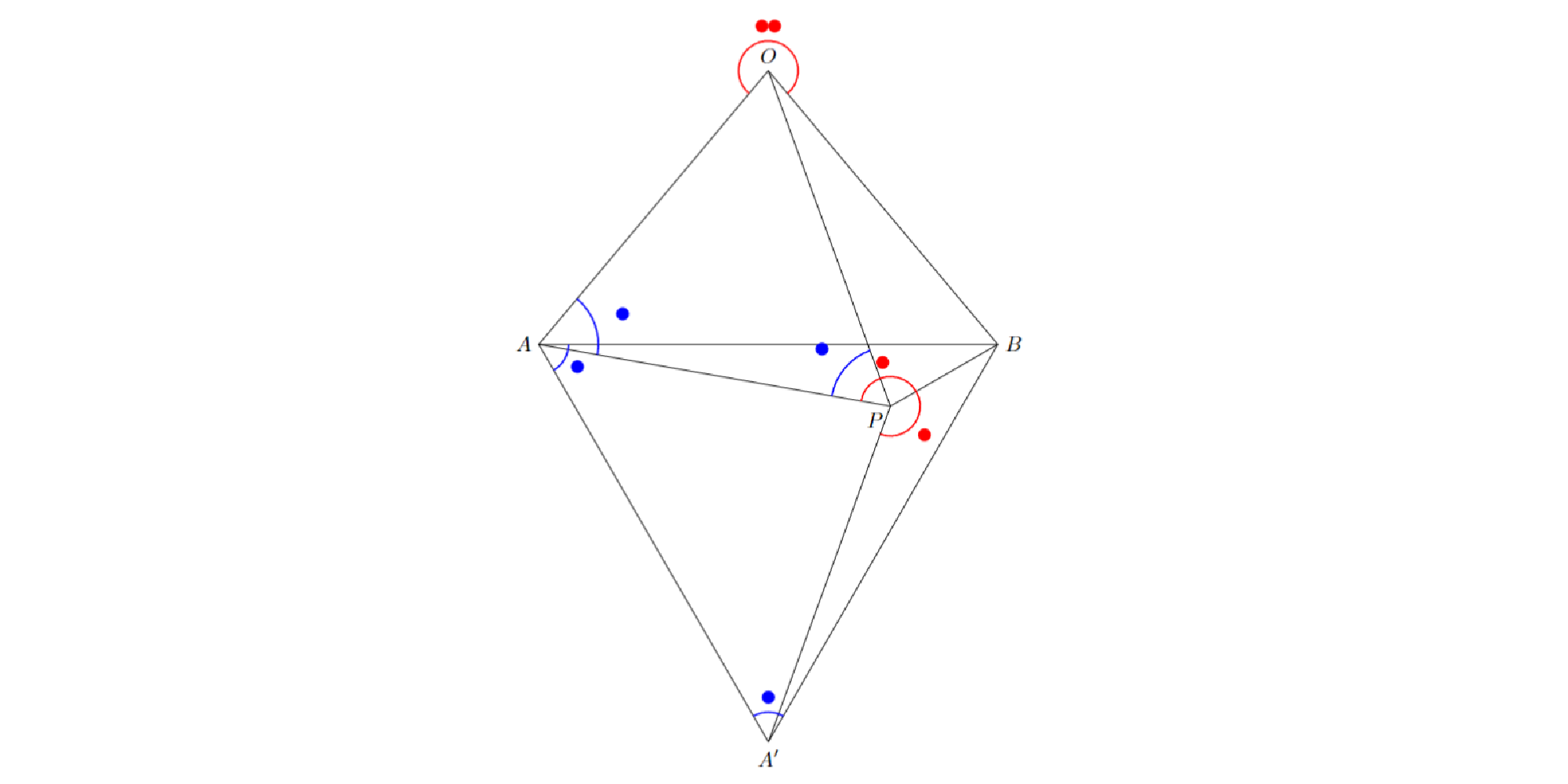 2.のとき
2.のとき
- 線分$AB$の上に点$O$があり,$∠APB$が$90^{\circ}$に等しいとき
直線$PB$に関して点$A$と対称な点$A^{\prime}$をとる.直線$PB$に関する対称性から以下が従う.
$$ \begin{eqnarray} ∠APB=∠A^{\prime}PB (1) PA=PA^{\prime} (2) ∠BAA^{\prime}=∠BA^{\prime}A (3) \end{eqnarray} $$
(1)から3点$A$,$P$,$A^{\prime}$は一直線上に並ぶ.(2)と$OA=OB$より三角形$BAA^{\prime}$と三角形$OAP$とは相似であるから,以下が従う.
$$ \begin{eqnarray} ∠BA^{\prime}A=∠OPA (4) \end{eqnarray} $$
(3)と(4)より
$$ \begin{eqnarray} ∠OAP=∠BAA^{\prime}=∠BA^{\prime}A=∠OPA \end{eqnarray} $$
であるから,三角形$OAP$は$OA=OP$の二等辺三角形であると分かり,$OP=OA=OB$を得る.
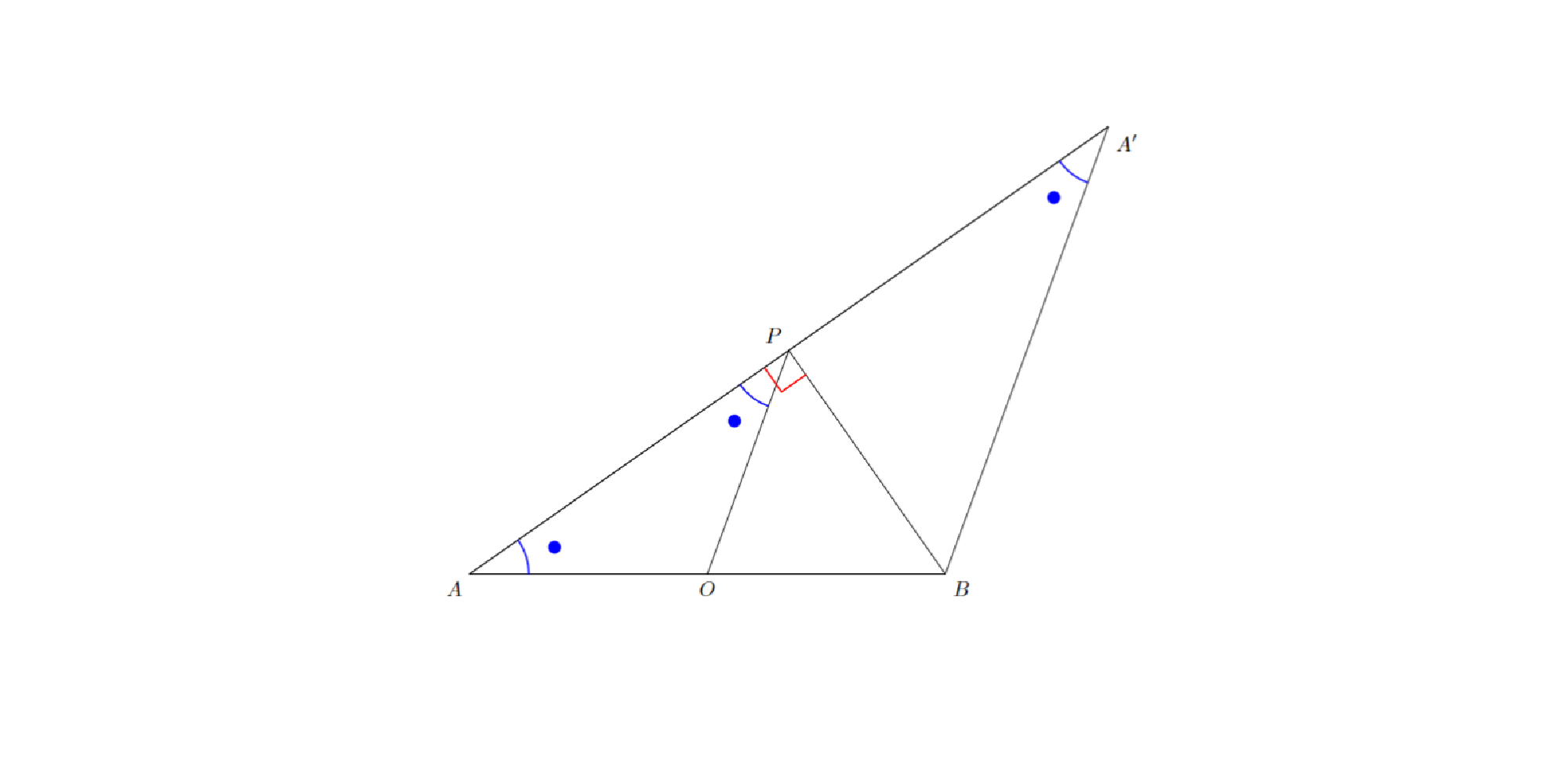 3.のとき
3.のとき
算数における円周角の定理の逆の使用例
堅苦しい数学の証明を見ても何も面白くないので,以下の算数の問題で実際に円周角の定理の逆を使ってみましょう.
問題:図のような四角形$ABCD$があり,$AB=AD$,$∠DAB=110^{\circ}$,$∠ABC=55^{\circ}$,$∠BCD=125^{\circ}$,$∠CDA=70^{\circ}$であるとします.このとき,$∠CAB$の大きさを求めてください.
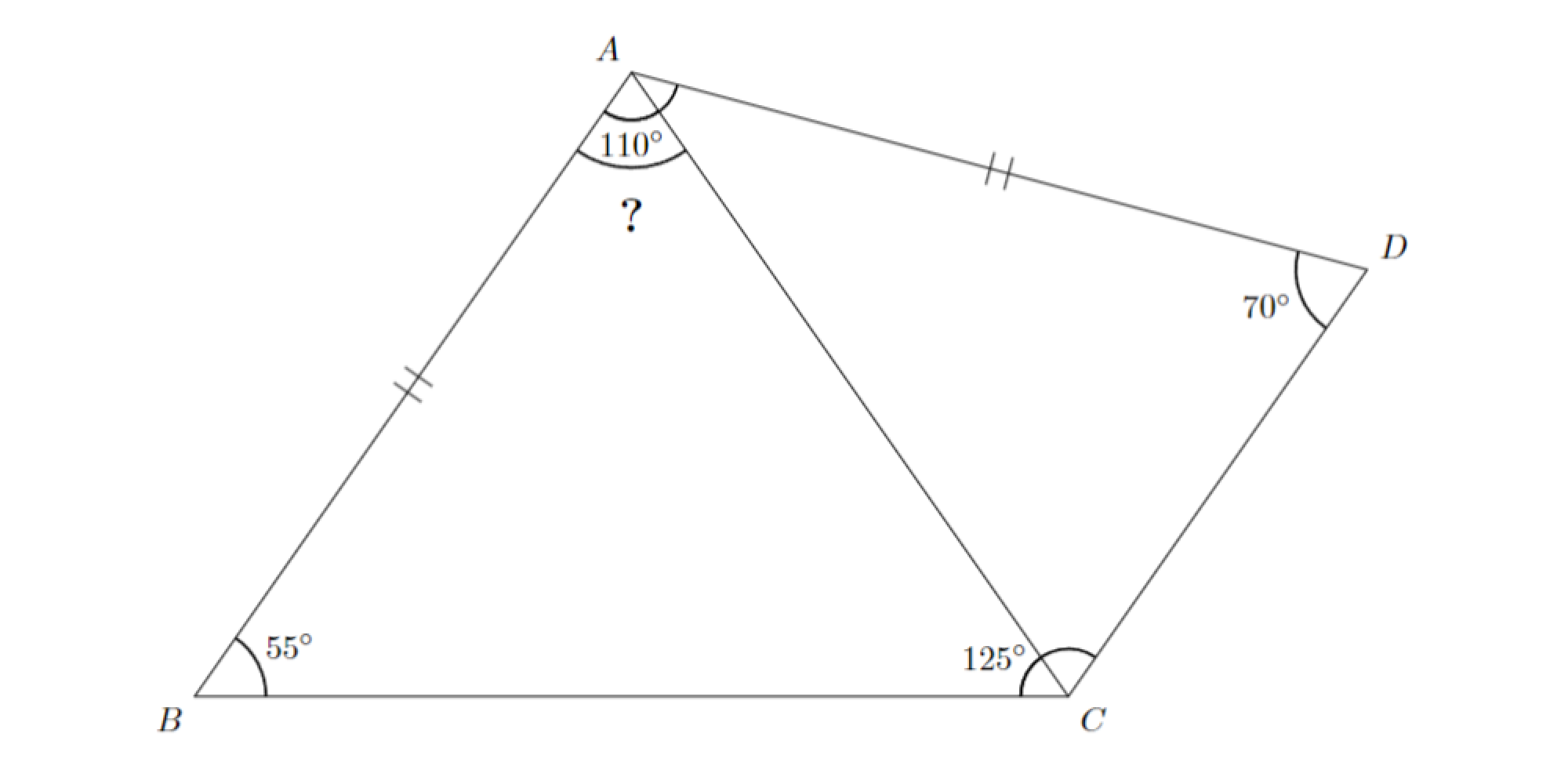 例2 問題
例2 問題
解答解説
線分$BD$をひき,辺$CD$に関して点$B$と対称な点$B^{\prime}$をとって角の大きさを決定すると,図のようになります.三角形$ABD$と三角形$CBB^{\prime}$とは3つの対応する角の大きさがすべて等しいので,相似になります.特に$AB:CB=BD:BB^{\prime}$であるので,これと$∠ABC=∠DBB^{\prime}$より,三角形$ABC$と三角形$DBB^{\prime}$とは相似になります.よって$∠CAB=∠B^{\prime}DB=70^{\circ}$であると分かります.
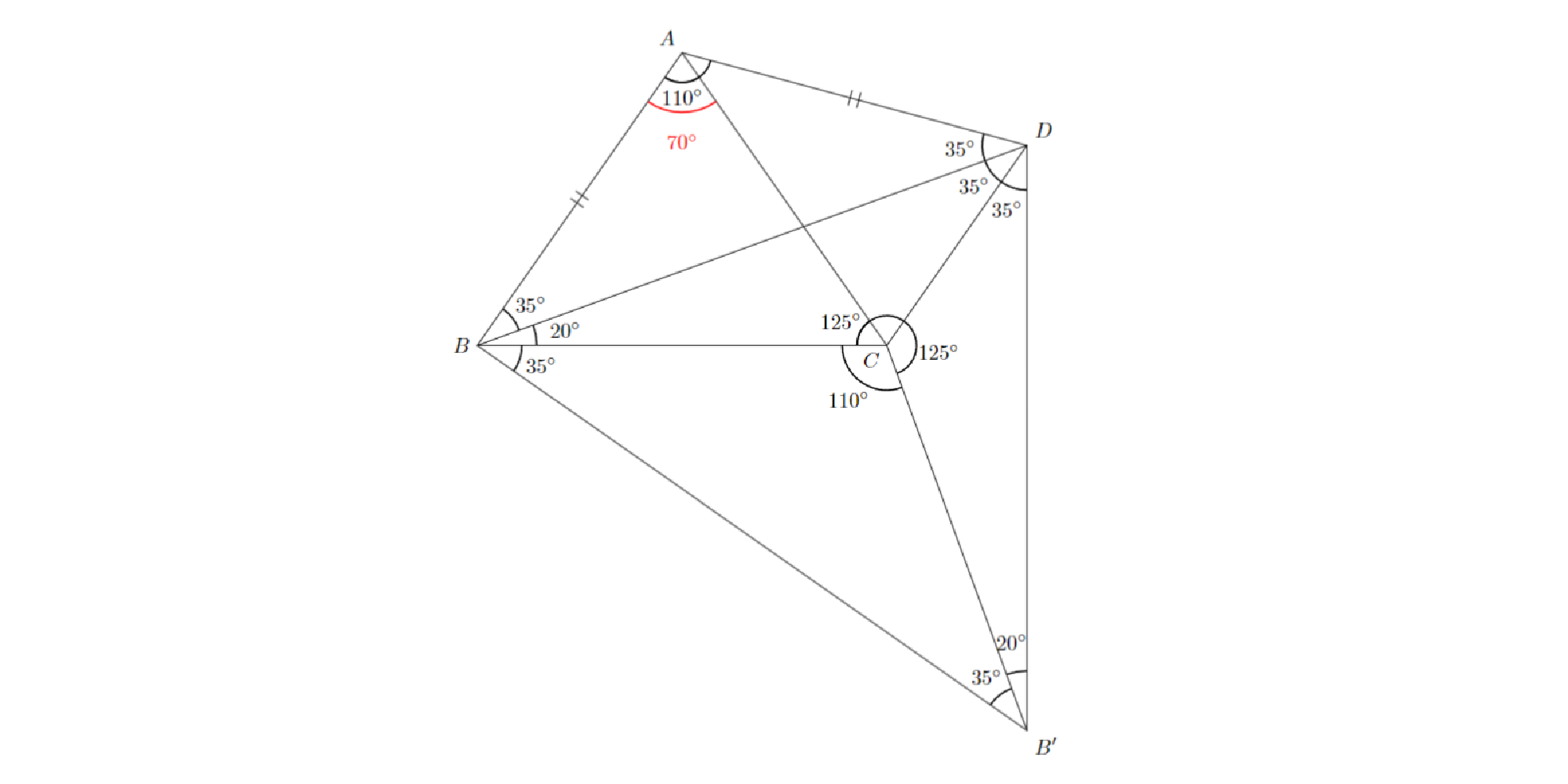 例2 解答解説
例2 解答解説
算数における円周角の定理とのつきあいかた
どのように接してあげれば良いのか
例1や例2のように,円周角の定理やその逆を使うことが分かりやすい場面はそれほど多くありません.では,実際に算数において円周角の定理やその逆と出会ったときに,どのように接してあげれば良いのでしょうか.突然話しかけられて「あれ,この人誰だっけな......」と思ってから「あ,円周角の定理(の逆)だ!」と思い出し,正しく接するまでの流れを,以下の問題で練習しましょう.
問題:四角形$ABCD$があり,$AB=CD$,$∠DAB=130^{\circ}$,$∠BDA=25^{\circ}$,$∠BCD=115^{\circ}$であるとします.このとき,$∠DBC$の大きさを求めてください.
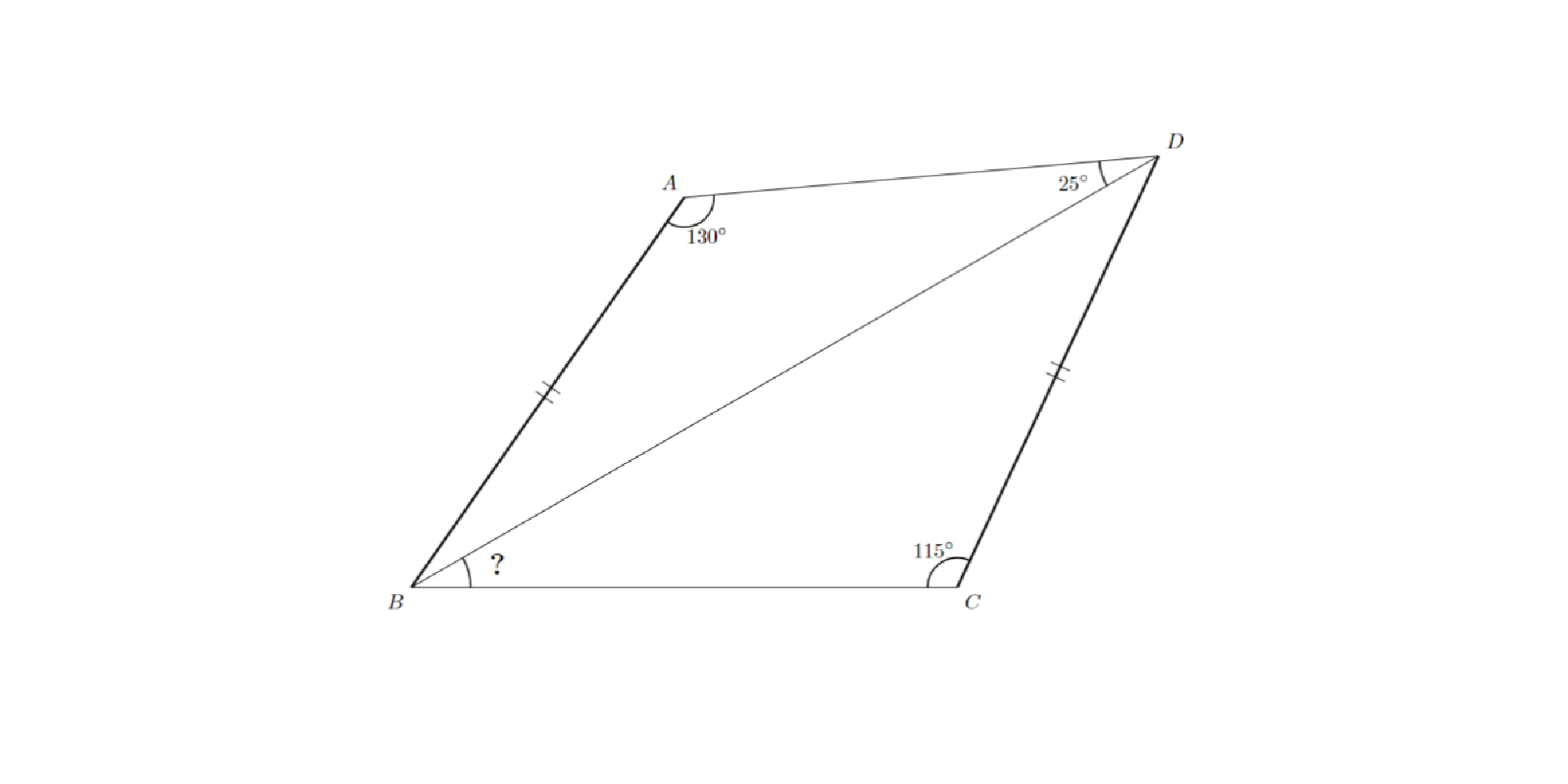 問題1 問題
問題1 問題
解答解説
角の大きさを決定すると図のようになり,$AB=AD=CD$であると分かります.
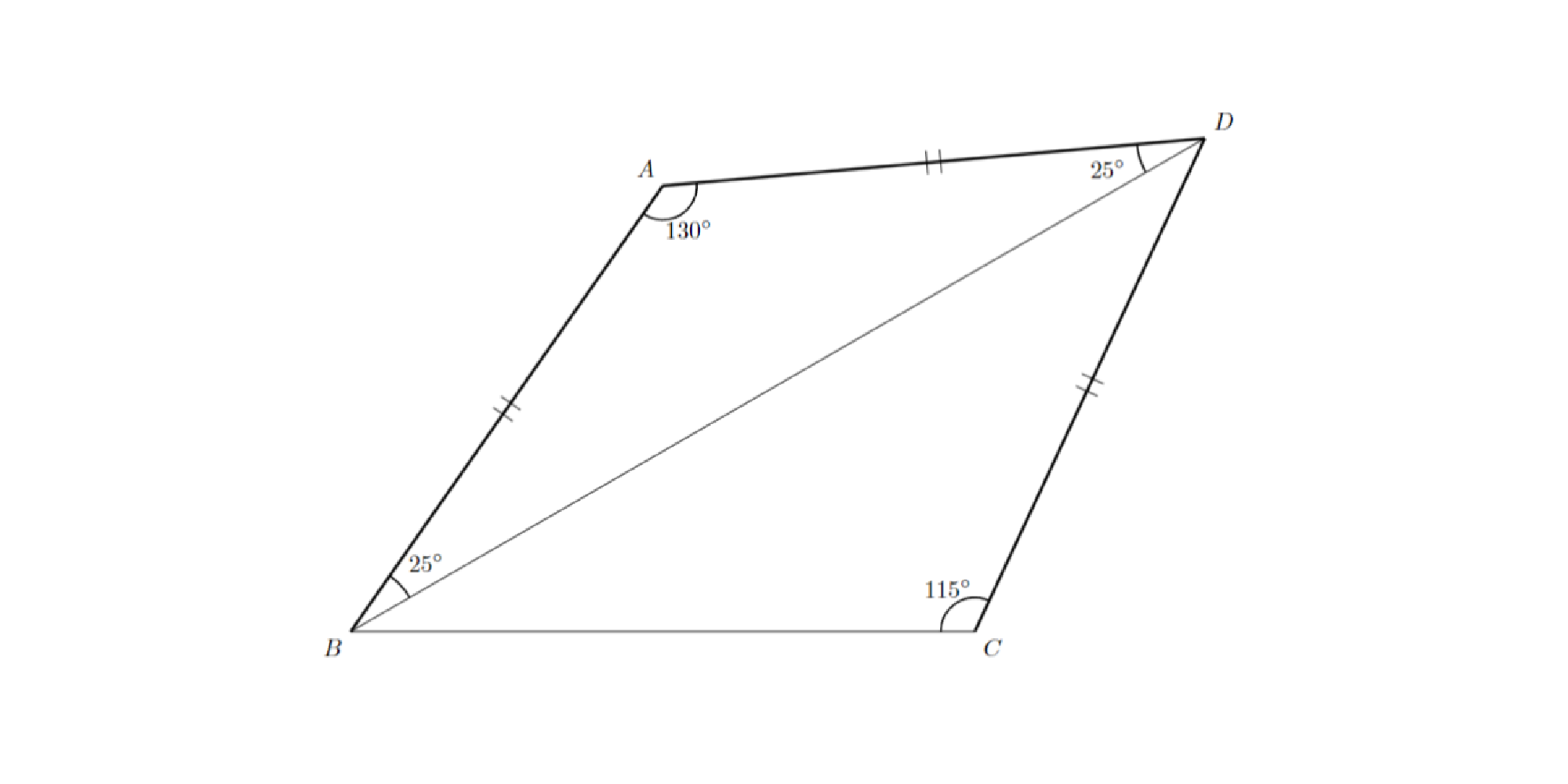 問題1 解答解説1
問題1 解答解説1
辺$BC$に関して点$D$と対称な点$D^{\prime}$をとって角の大きさを決定すると図のようになり,$AB=CD^{\prime}$,$AD=CD$となります.
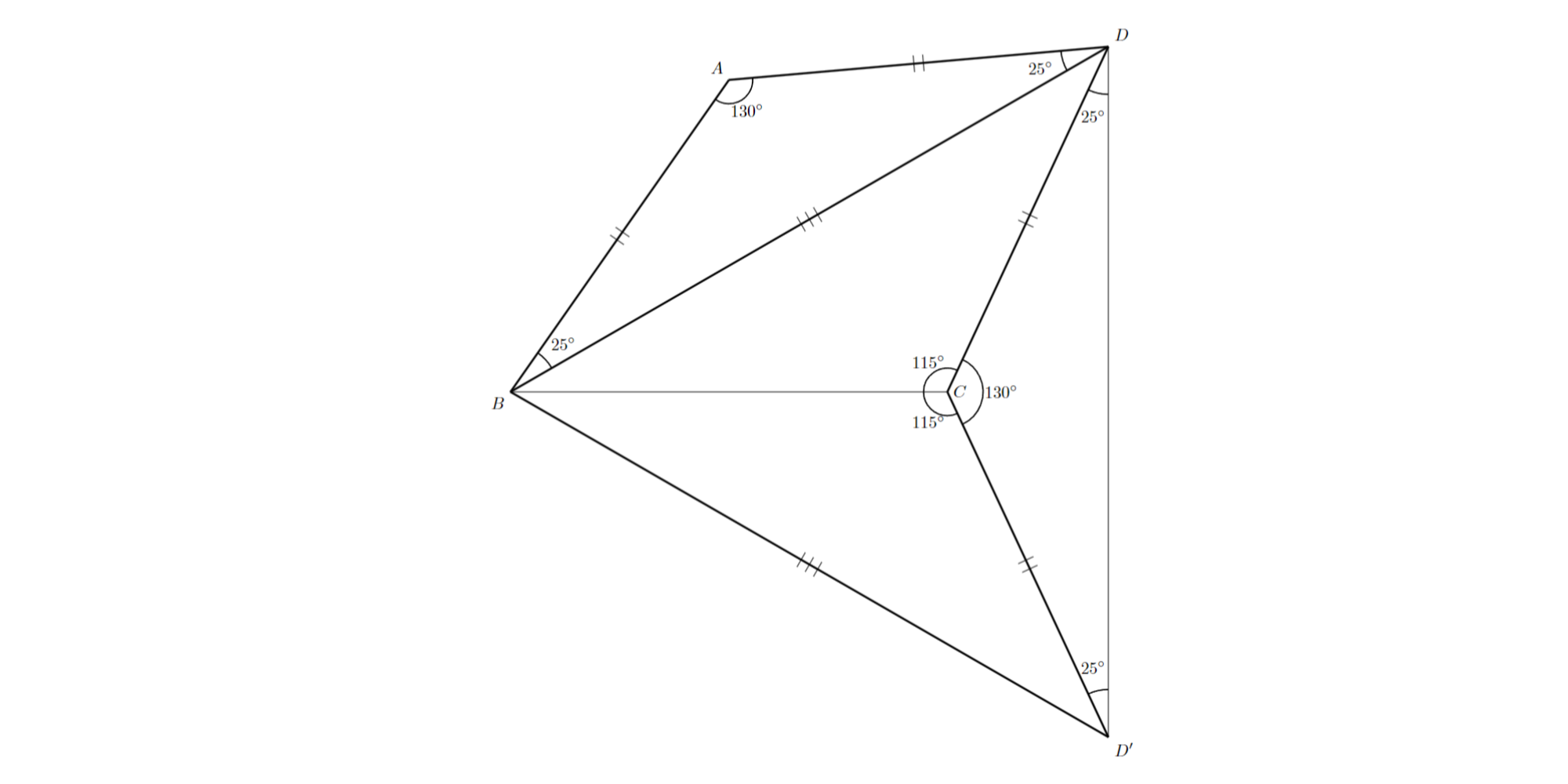 問題1 解答解説2
問題1 解答解説2
$AB=CD^{\prime}$,$AD=CD$,$∠DAB=∠DCD^{\prime}$より三角形$ABD$と三角形$CD^{\prime}D$とは合同であると分かるので,特に$BD=D^{\prime}D$となります.以上より$BD=D^{\prime}D=BD^{\prime}$であるので,図のように三角形$BDD^{\prime}$は正三角形であると分かり,直線$BC$に関する対称性より$∠DBC=30^{\circ}$であると分かります.
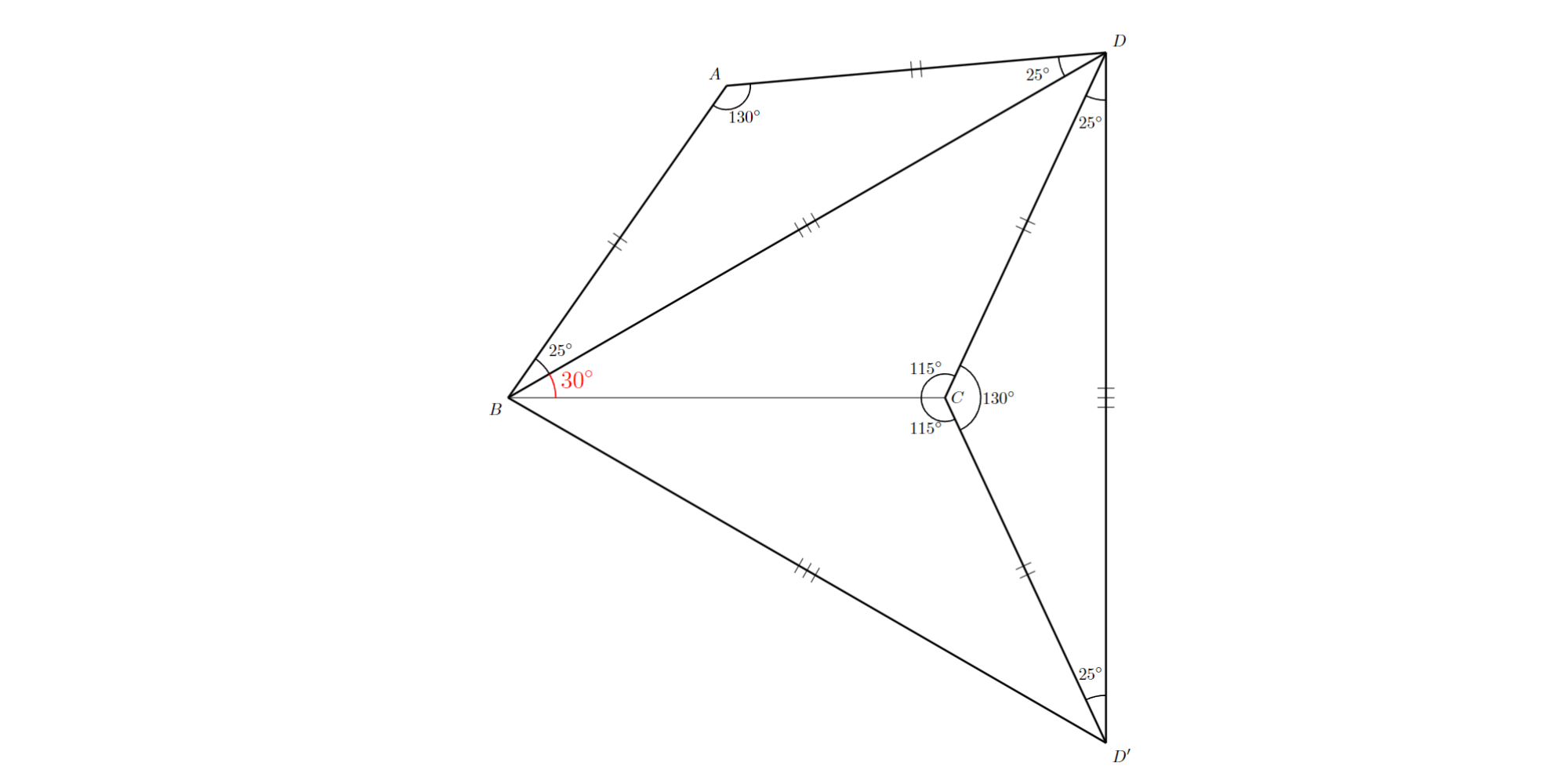 問題1 解答解説3
問題1 解答解説3
問題:四角形$ABCD$があり,$AB=AD=10\mathrm{cm}$,$∠DAB=80^{\circ}$,$∠ABC=75^{\circ}$,$∠BCD=140^{\circ}$,$∠CDA=65^{\circ}$であるとします.図のように直角三角形$BCE$をとったとき,この直角三角形$BCE$の面積を求めなさい.
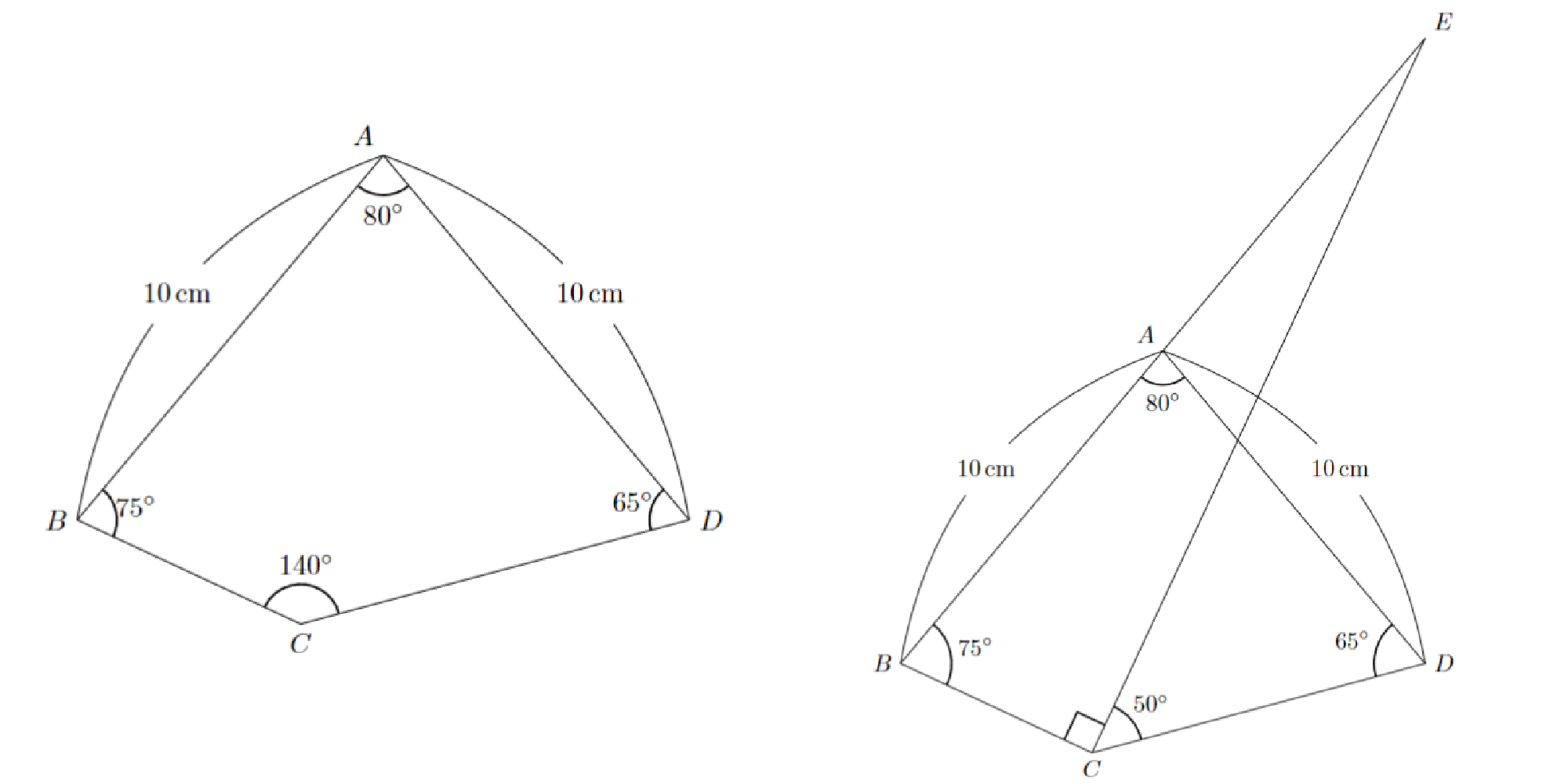 問題2 問題
問題2 問題
解答解説
線分$BD$をひき,辺$CD$に関して点$B$と対称な点$B^{\prime}$をとって角の大きさを決定すると,図のようになります.三角形$ABD$と三角形$CBB^{\prime}$とは3つの対応する角の大きさがすべて等しいので,相似になります.特に$AB:CB=BD:BB^{\prime}$であるので,これと$∠ABC=∠DBB^{\prime}$より,三角形$ABC$と三角形$DBB^{\prime}$とは相似になります.よって$AC=AB$であると分かります.
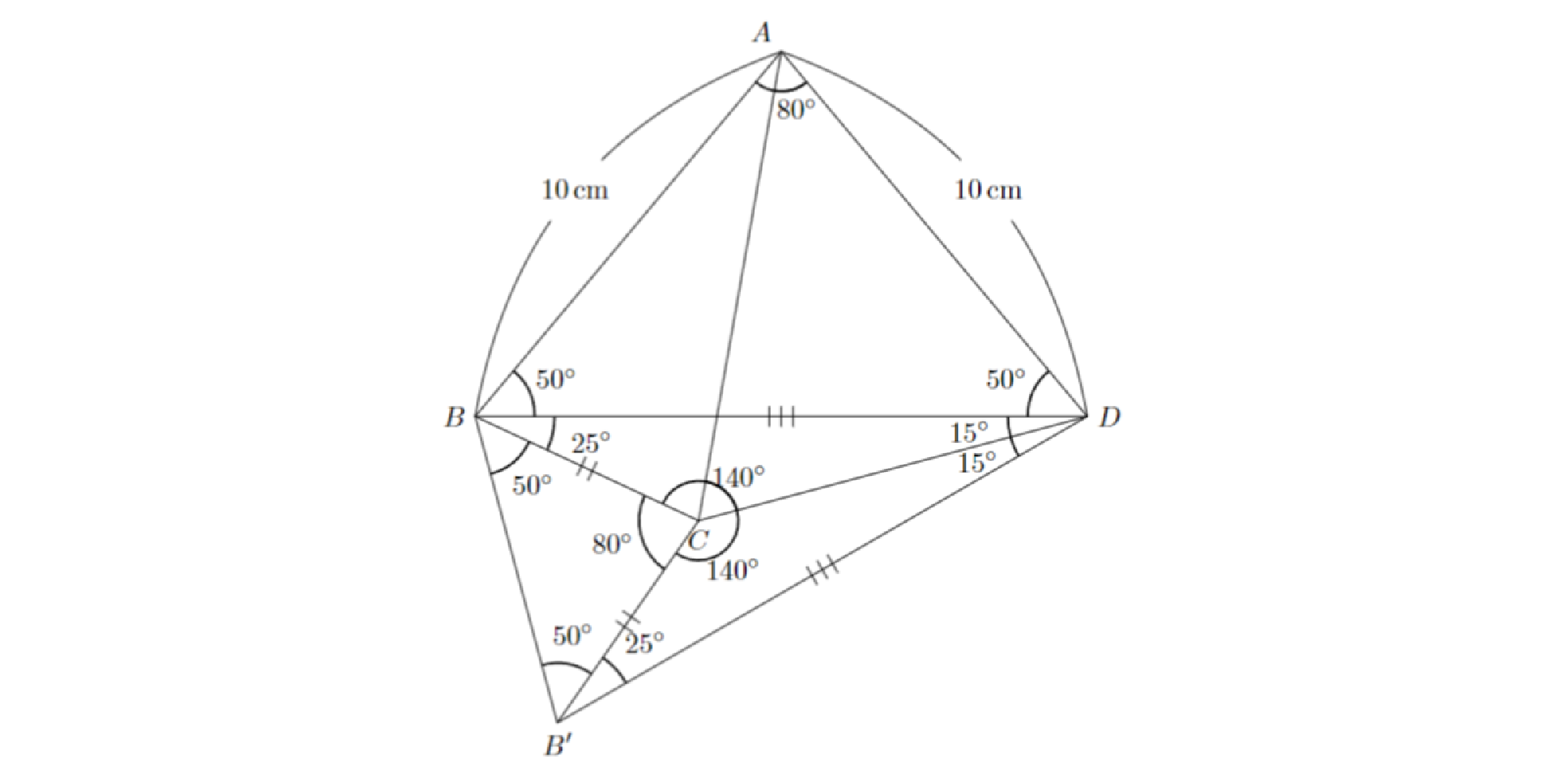 問題2 解答解説1
問題2 解答解説1
$AC=AB$に注意して角度を決定すると図のようになり,$AE=AC=AB=10\mathrm{cm}$であると分かります.点$C$から辺$BE$へと下ろした垂線の足を点$H$とすると,図のような正三角形$ACC^{\prime}$を考えることで$CH=5\mathrm{cm}$であると分かります.よって三角形$BCE$の面積は
$$
\begin{eqnarray}
20\mathrm{cm}\times5\mathrm{cm}\times\frac{1}{2}=50\mathrm{cm}^2
\end{eqnarray}
$$
より$50\mathrm{cm}^2$と分かります.
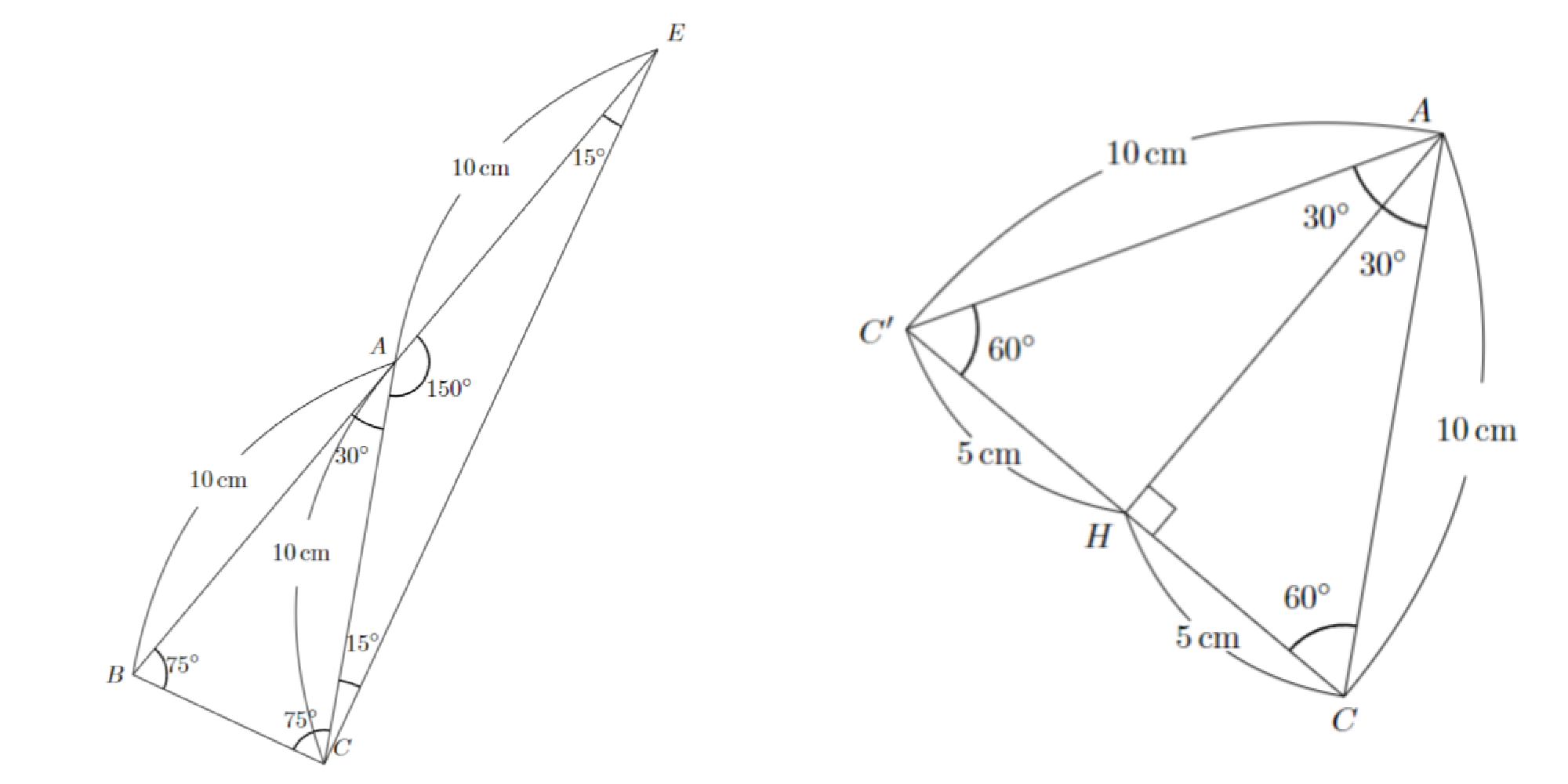 問題2 解答解説2
問題2 解答解説2
自分から話しかけに行っても良いのだろうか
最後に,円周角の定理やその逆に,こちらから話しかける練習をしましょう.一見円周角の定理やその逆が利用できなさそうな場面でも,補助線等によってこれらが使用できる状況を作ることで,問題の本質を掴めることがあります.はじめは到底思い付かない一手に見えても,それがいつかあなたの算数を助けてくれるかもしれません。
問題:三角形$ABC$の内部に,$OA=OB=OC$となるように点$O$をとったところ,三角形$OAB$,三角形$OBC$,三角形$OCA$の面積はそれぞれ$19.8\mathrm{cm}^2$,$13.8\mathrm{cm}^2$,$19.2\mathrm{cm}^2$となりました.三角形$ABC$の内部に$∠PAB=∠OAC$,$∠PBA=∠OBC$となるように$P$をとったとき,三角形$PAB$の面積を求めなさい.
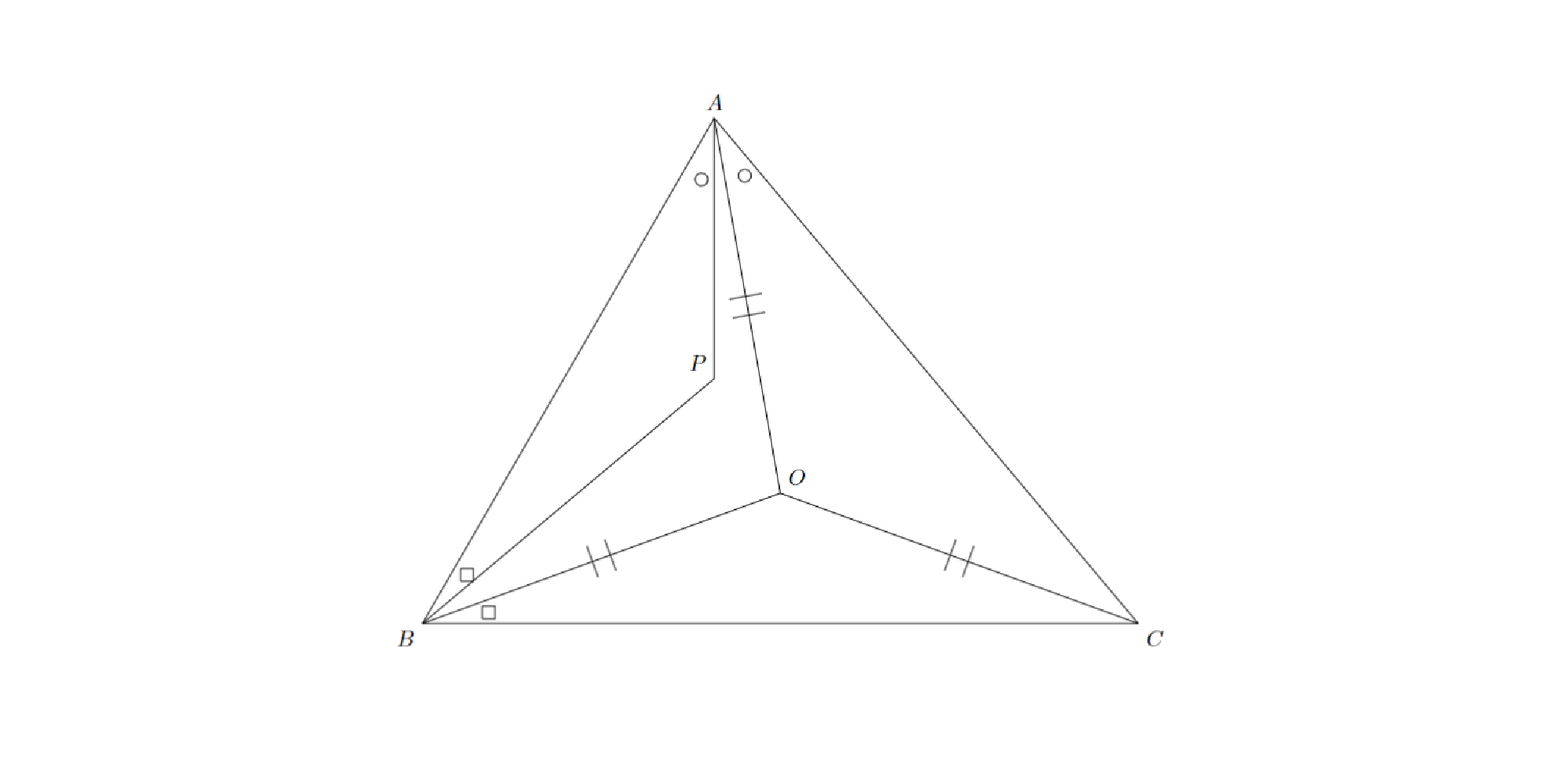 問題3 問題
問題3 問題
解答解説
図のように三角形$ABP$を移動させて,三角形$BAQ$をとります.
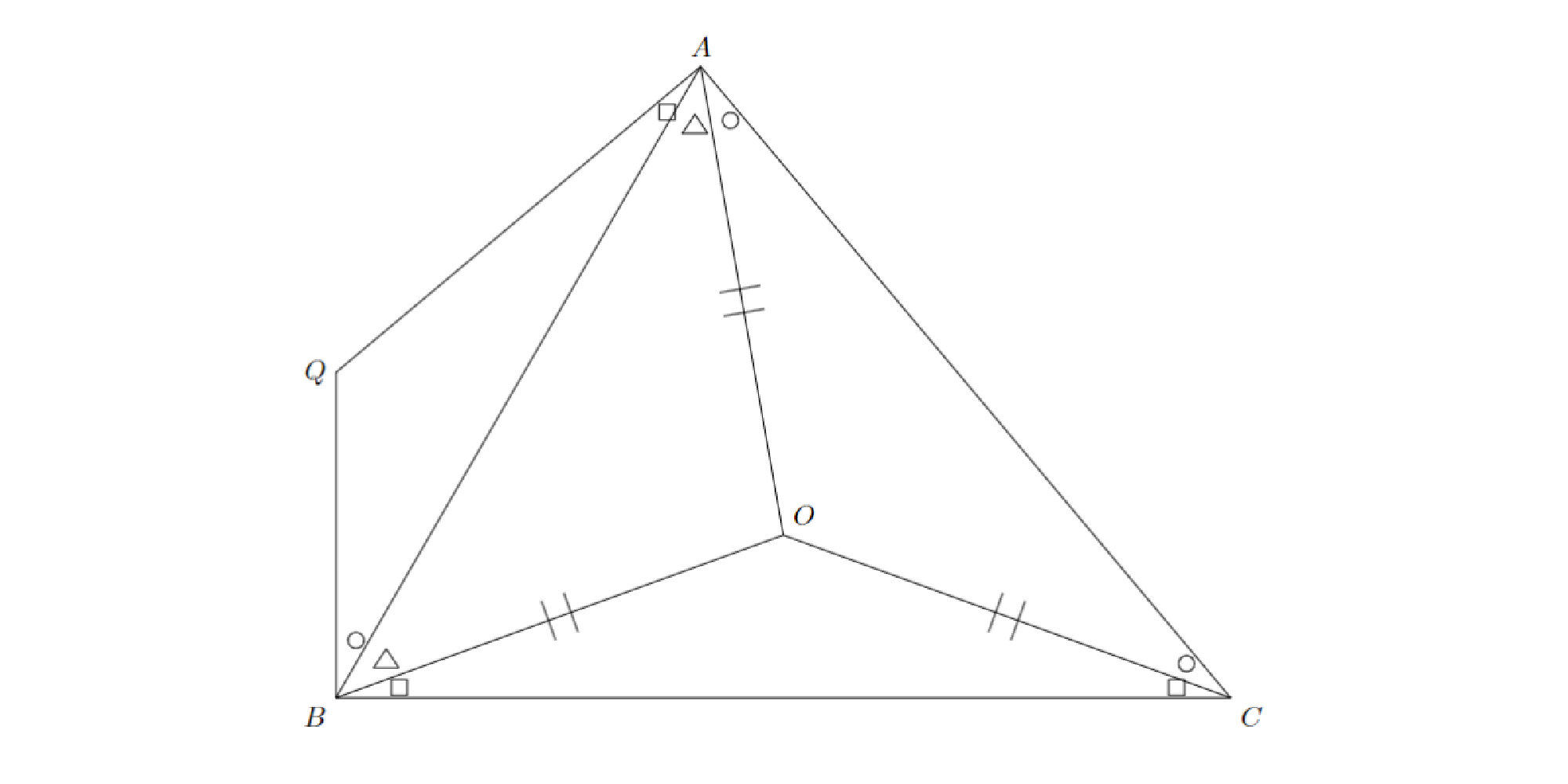 問題3 解答解説1
問題3 解答解説1
線分$BQ$に関して点Aと対称な点$A^{\prime}$をとって角の大きさを決定すると,図のようになります.
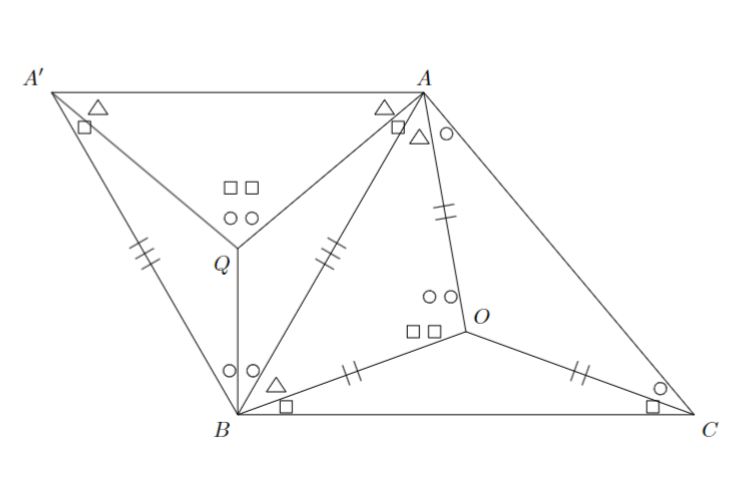 問題3 解答解説2
問題3 解答解説2
三角形$OAB$と三角形$QAA^{\prime}$とは3つの対応する角の大きさがすべて等しいので,相似になります.特に$OA:AB=QA:AA^{\prime}$であるので,これと$∠OAQ=∠BAA^{\prime}$より,三角形$OAQ$と三角形$BAA^{\prime}$とは相似になります.特に$OA=OQ$,$∠QOA=∠A^{\prime}BA$であると分かります.
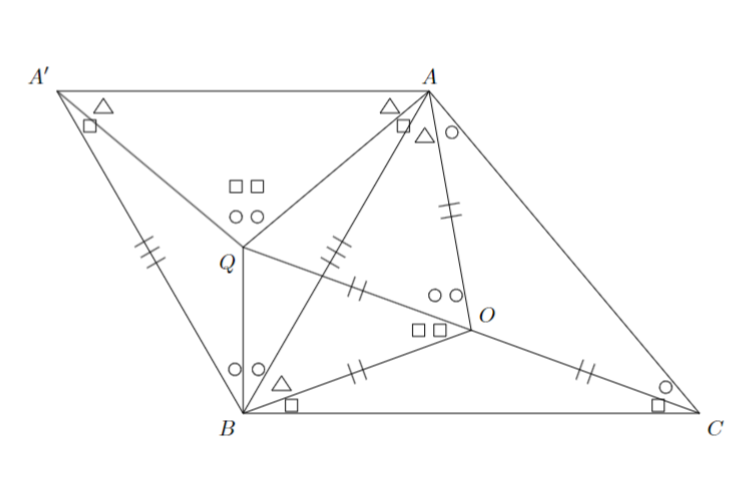 問題3 解答解説3
問題3 解答解説3
このとき外角の性質から3点$C$,$O$,$Q$は一直線上に存在し,特に$OQ=OC$から点$O$は線分$CQ$の中点であると分かります.このとき三角形$PAB$の面積が以下のように求められます.
$$
\begin{eqnarray}
\Delta PAB&=&\Delta QBA\\
&=&\Delta OAQ+\Delta OBQ-\Delta OAB\\
&=&\Delta OAC+\Delta OBC-\Delta OAB\\
&=&19.2\mathrm{cm}^2+13.8\mathrm{cm}^2-19.8\mathrm{cm}^2\\
&=&13.2\mathrm{cm}^2
\end{eqnarray}
$$
問題:三角形$ABC$があり,内部の点$D$が,点$A$から辺$BC$へと下ろした垂線$AE$上にあるとします.$∠ABD=30^{\circ}$,$∠DBE=50^{\circ}$,$∠DCE=30^{\circ}$であるとき,$∠CAD$の大きさを求めてください.
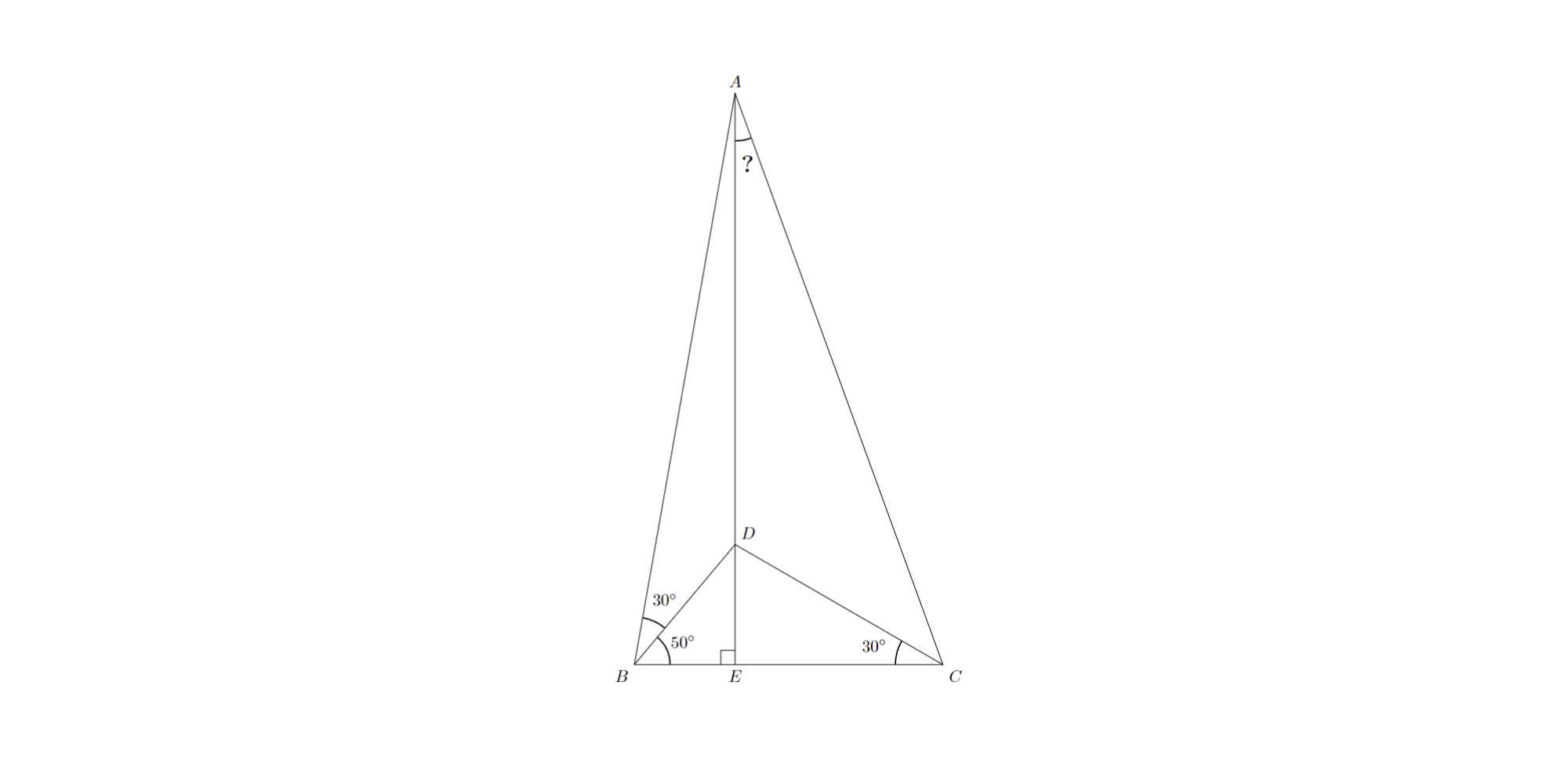 問題4 問題
問題4 問題
解答解説
図のように正三角形$ADF$をとります.
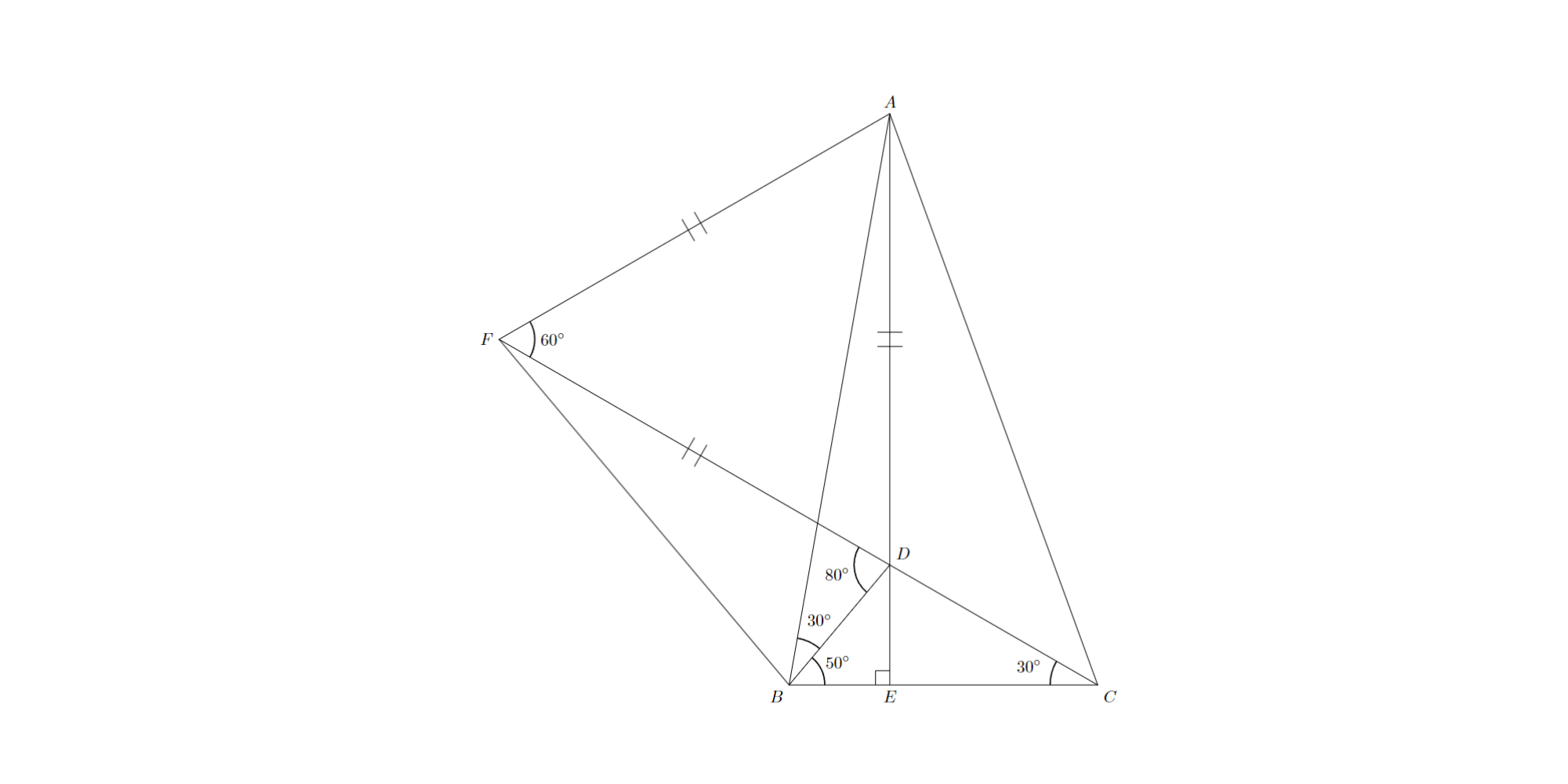 問題4 解答解説1
問題4 解答解説1
$∠AFD=60^{\circ}$,$∠ABD=30^{\circ}$より,円周角の定理の逆から$FB=FD$と分かります(Check by yourself).ここから角の大きさを決定し,辺$BC$に関して点$D$と対称な点$D^{\prime}$をとると,3点$F$,$B$,$D^{\prime}$は一直線上に存在することが分かります.
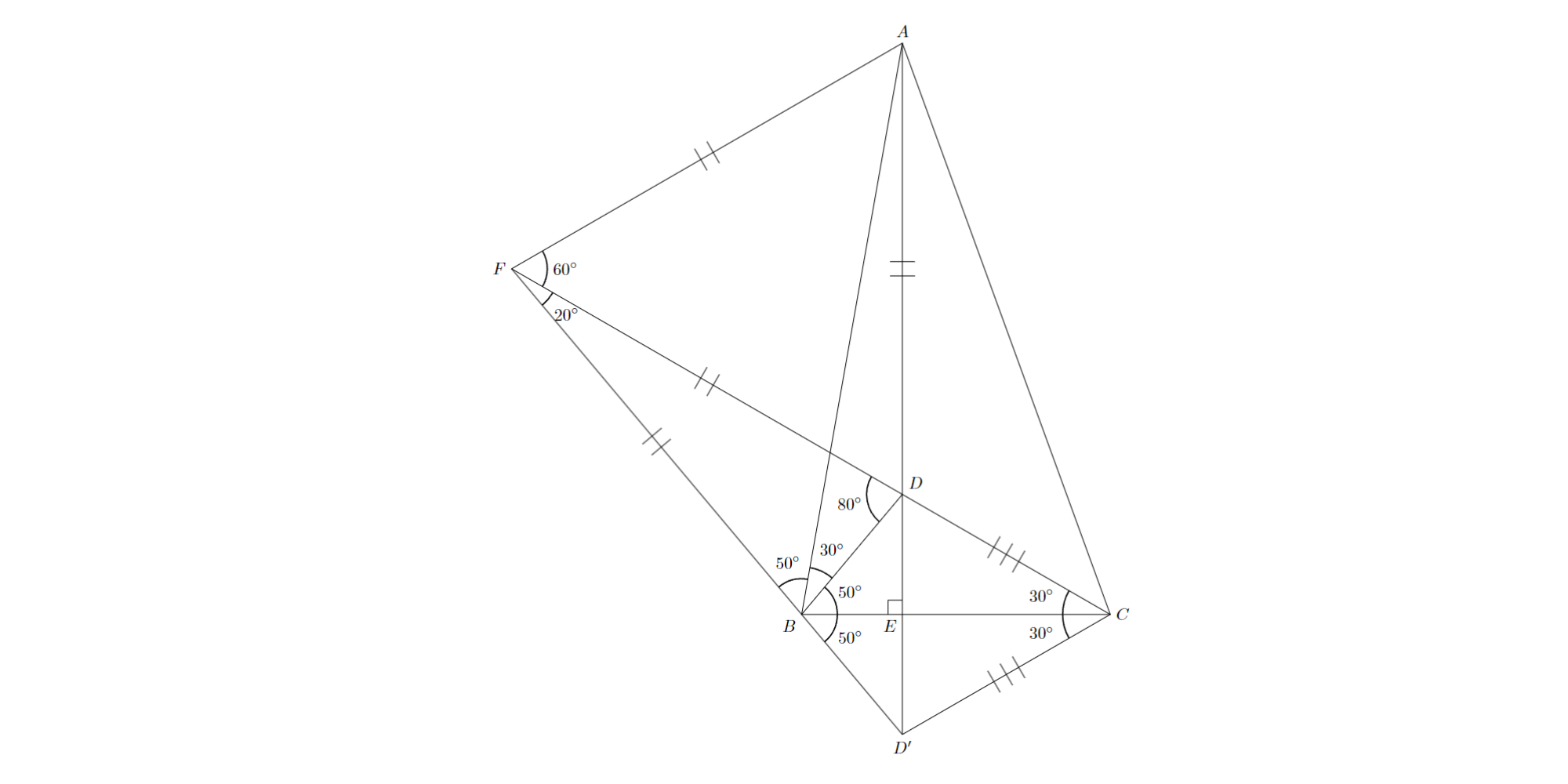 問題4 解答解説2
問題4 解答解説2
三角形$CDD^{\prime}$は正三角形になるので,図の点線に関する対称性に気が付き,$∠CAD=∠D^{\prime}FD=20^{\circ}$であると分かります.
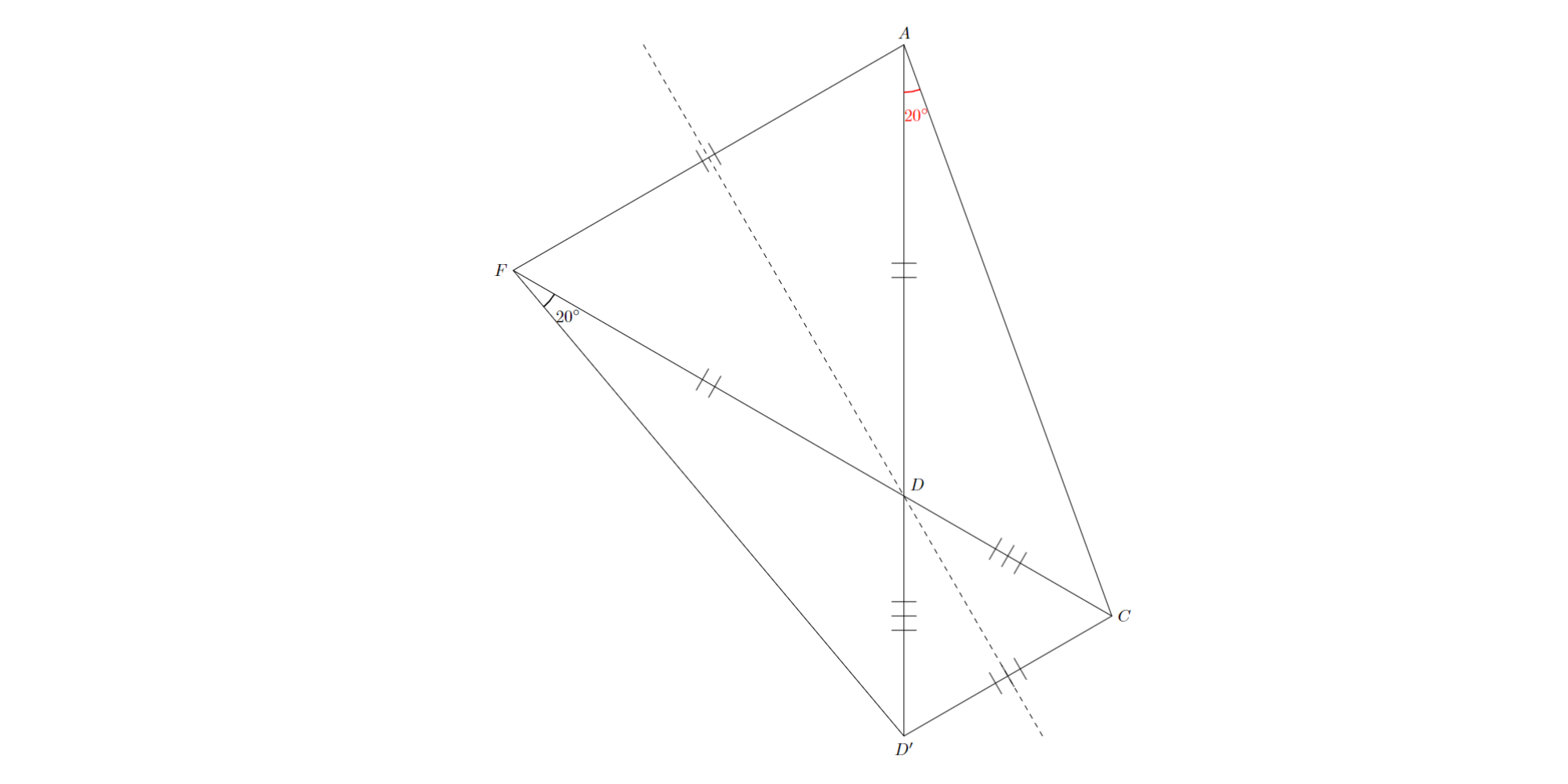 問題4 解答解説3
問題4 解答解説3
今日の算数
お疲れさまでした.恒例の今日の算数を出題して記事を終わりたいと思います.今日学んだ解法を使って解ければ良いですね.解答お待ちしております.
問題:図のような三角形$ABC$と3つの正三角形$ABD$,$BDE$,$DEF$があり,$∠ACF=∠BCF=30^{\circ}$であるとします.このとき,三角形$ABC$の面積は正三角形$ABD$の面積の何倍ですか.
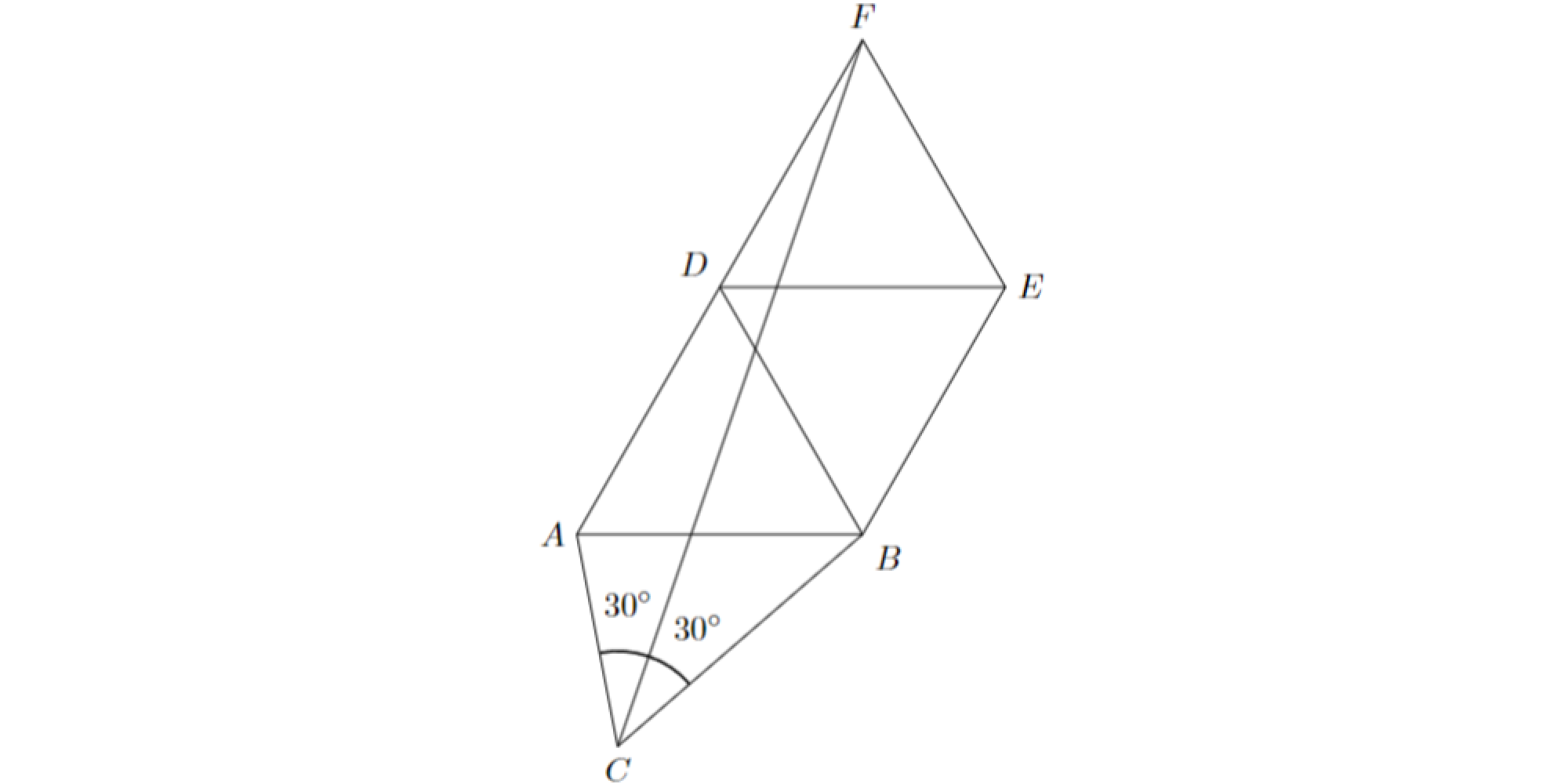 今日の算数 問題
今日の算数 問題
