幾何の好きな話題を話す！(Advent math calendar 2023)

こんにちは！らぐねるです。これは AMC(Advent Math Calendar)2023 の記事になります．何かテーマを1つに決めようと思ったのですが、決めきれなかったので、その時に書きたい！と思ったことを気まぐれで書いていこうと思います．結構めちゃくちゃな記事ですがどこでもいいので良いと思った部分があれば嬉しいです．

1.作図の大切さについて

　皆さんは幾何の作図のことをどのように考えているでしょうか？僕は作図は幾何を解く上での半分を占めていると思っています．というのも，多くの問題において，キーとなる性質や非自明な性質は正確な図を描くことで予想できることが多いからです．確か、「三角形と円の幾何学」という本にも「初等幾何の問題を解く上での基本は，正確な図を描き，等しそうな辺や角を探してみる」といったようなことが書かれていたような気がします．さらに，正確な図を描くことができないと，誤った議論にも繋がってしまいます．僕は問題文で与えられた条件から、証明に必要な非自明な性質を知らない状態から導き出すのが苦手なので，作図を正確に行って，成り立ちそうな性質を予想して見通しを立てるということを意識して幾何の問題を解いています．その点では，フリーハンドで図を書いてバシバシ問題を解いていく人には本当に頭が上がりません．そういう方はこの記事をすべて読み飛ばして、幾何のコツを教えてほしいです（）．

　作図をする上での基本的なポイントは大きく分けて以下の3つです．

1. できるだけ正確な図を描くこと
2. 特別な場合の図を描かないこと
3. 2つ以上の図を描くこと

　1は言わずもがなですね．
　2は，例えば三角形$ABC$を二等辺三角形でないのに二等辺三角形に見えるようにして図を描いてしまった場合，その図から条件を予想しようとすると，二等辺三角形だから成り立っている性質も予想に含んでしまう可能性があるということです．他にも，例えばある角が$60^{\circ},90^{\circ},120^{\circ}$ の場合などもいらぬ辺が等辺になってしまう可能性などが考えられます．
　3は，単純に2つ以上の図を描くことで予想の精度をあげられるということです．「この三角形$2$つはこっちの図だと相似に見えるけど，こっちの図だと相似に見えないから違うな」とか，「どちらの場合でもこの直線がこの点を通ってるからこれは成り立ちそう」といったムーブができるようになります．この場合極端に問題の三角形などの角度とかを変えた図を描くと良いでしょう．

何を予想するか？

　僕が意識しているのは次のようなポイントです．

• ある2つの辺の関係（一方の辺の長さが片方の辺の整数倍になっているなど）
• ある2つの直線の関係（平行、垂直など）
• 3つの直線の共点
• 2つの直線と1つの円の共点
• 特別な点（外心、内心など）がある直線上にある
• 2つの三角形、四角形の関係（相似，合同など）

作図のちょっとした小ネタ

　以下では作図を正確にする上での小ネタを書いていきます．めちゃくちゃ基本的なこと＋しょうもないことが多いので各自適当に読み飛ばしてください．

三角形は外接円を描いてから描く

　三角形ABCを描くときはまず円を描いて，そこに3つの点を取りましょう（そうしないほうがいい例外はありますが）．問題文中に外接円が出てこない場合でも描きましょう．多くの問題では外接円は使いますし，外接円が書いてあると他のオブジェクトを描きやすいです．

中点はコンパスのみで取る

　線分の中点は，線分の中点ぽい所にコンパスの針を差し，そこからコンパスを回したときに線分の端点が円上に来るように中心を微調整していき、ちょうどいいところで針のところに印をつければいい感じに取れます（）．効率悪そうですがめちゃくちゃ正確に書けるのでおすすめです．

外接円は本当にきれいに書く

　個人的な感想ですが，外接円のズレはかなり後の作図に響く印象です．しっかりコンパスの先端が３点すべてにぶち当たるように書きましょう．

内心，傍心はトリリウムの定理から描く

　 トリリウムの定理 を使うと、二等分線を1回引いて外接円との交点をとり，コンパスを回すだけできれいに内心，傍心を描けます．二等分線は作図をする上で普通に描くとコンパスを3回使わないといけない厄介者です．できるだけ節約していきましょう．
　もっと言うとこの二等分線も、先述したように外接円が描いてあれば，辺の垂直二等分線（辺の中点と外心を結べば良い）と外接円の交点を取り，その辺と対する頂点と交点を結ぶことで実質コンパス1回で描くことができます．

垂心はまずある辺を直径とする円を描く

　三角$ABC$の垂心を書くとき，まず$BC$を直径とする円を書いて，その円と$AB，AC$が交わる点を$E,D$として、$BC$と$CE$の交点を取れば描けます．他にも楽な方法があるかもしれませんが、個人的にはこれが一番だと思っています．

傍心が3つ出てきたら傍心から描いて作図する

　有名事実として三角形$ABC$の傍心$3$つからなる三角形の垂足三角形（各頂点から対辺に下ろした垂線の足$3$つからなる三角形）は三角形$ABC$となります．これを用いると傍心を先に描いて垂心を描き，垂足三角形を描いたほうが素直に傍心を$3$つ書くより断然早くて正確、ということになります．三角形$ABC$の外接円は傍心$3$つからなる三角形の九点円なので，傍心三角形の垂心，外心を取ってその中点を取れば楽に描けます．

描く順番を工夫する

　これは「獲得！金メダル！」とかにも書いてあったと思います．「点Xをとったところ，～となった」という問題では描く順番を工夫すると正確な図を描くことができることが多いです．例えば OMC186-(E) などがあります．この問題は正確な作図がぶっ刺さる問題の一つです（面白いので解いてみてください）．この問題では$E,F,P,Q,R$ の順に点を取ろうとすると$DQ=DR$を作図できません．僕が ユーザー解説 （ネタバレ要素を含みます）に書いているような順番にすると問題の性質を保ったまま綺麗に描くことができます．この作図の場合では少し幾何的な考察も挟む必要があるのですが，それは次で説明します．

描く前に幾何的な考察を挟んでみる

　先程言ったように描く前に少し幾何的な考察を挟んでみるときれいな作図法が見つかるかもしれません．例えば，次の問題があります．

　この図を考察無しでいきなり描こうとすると無理でしょう．しかし $∠A = ∠C = ∠E$ と $∠B = ∠D = ∠F$ という条件をうまく解きほぐす（ネタバレになるので言えませんが）と$∠A, ∠C, ∠E$ の二等分線が一点で交わるという条件を消せばこのような六角形をきれいに描けます．

　先程ネタバレになるので言えないと言いましたが，作図が難しい問題では，作図法を考えてみることで問題の条件をうまく言い換えできることが多いです（当たり前ですが）．作図が難しい問題ではまず幾何的な考察をして作図法を考えてみるのも良いでしょう．

実際に問題を解く過程（USA TSTST 2022-6)

　最後に，僕がどうやって幾何を解いているかというのを思考過程を含めて描きたいと思います（ネタバレです）．以下は僕のお気に入りの問題の一つです．

　まずは図を丁寧に描きます．（不必要な線が混じっていますが気にしないでください．）

USATSTST 2022-6

　$4$点の共円を示す方法は次の$3$つがほとんどです．

1. 内接四角形の対角の和が$180^{\circ}$であることを使う
2. $4$点を結ぶ線分のうち$3$つの垂直二等分線が$1$点で交わることを示す
3. $4$点のうちある$1$点で反転し，他の$3$つの像が共線であることを示す
4. $4$点のうちにない$1$点で反転し，4点の像が共円であることを示す

　この問題では何が使えそうかなぁと考えます．まず$X_A,Y_A$が曲者なので反転はちょっと面倒くさそうです．次に$1$ですが，ここで考えるのは対称性です．この問題では$K_A,K_B,K_C$の点の取り方に対称性がありますが，$1$をやろうとするとこの対称性を崩すことになってしまいます．そもそも図がきつそうなのでやる気は起きないでしょう．一方$2$だと$OK_A,OK_B,OK_C$の垂直二等分線の共点を示せば良いので，対称性を保ったまま証明を続けられます．ということで$2$を採用することになります．このような対称性の使い方は重要です．

　$OK_A,OK_B,OK_C$すべてを同時に考えるのはだるすぎるので，まず$OK_A$についてのみ考えていきます．$(OX_AY_A)$の中心を$A_1$, $(OBC)$ の中心を$A_2$とします．$OK_A$の垂直二等分線は直線$A_1A_2$です．というわけでこれを適当に延長してみます．するときれいな図を描いているので，これが$A$を通りそうだということが予想できます．（実際には２つ図を書いて予想の正当性を確認しています）これを示せたら，対称性より コスニタの定理 を使って決着となります（知らなくても複素で示せます）．

　したがって$A$を通ることを示しに行きます．ここで結論からの逆算を考えてみます．$A$を通ると仮定したら，一体何が見えるでしょうか・・・そうです，相似拡大です．$AX_AY_A$と$ABC$が相似なのでもろに相似拡大が刺さります．こういう考えができるのが予想の強いところですね．

　あとは仕上げですね．$A$を中心とする相似拡大で$(A_1)$が$(A_2)$にうつることを示せばいいです．これには色々なやり方がありますが，僕は長さ計算で示しました．$AO$が$(A_2)$と再び交わる点を$L$とします．$(A_2)$に対する$A$の方べきの値を求めて$AL$の長さを求め，$AY_A:AC=AO:AL$を示す方針です．それほど多くない計算量でできます．普通に初等幾何でも示せます．よかったら考えてみてください．

　

　

2.IMO2015-3のオリジナル解法および一般化

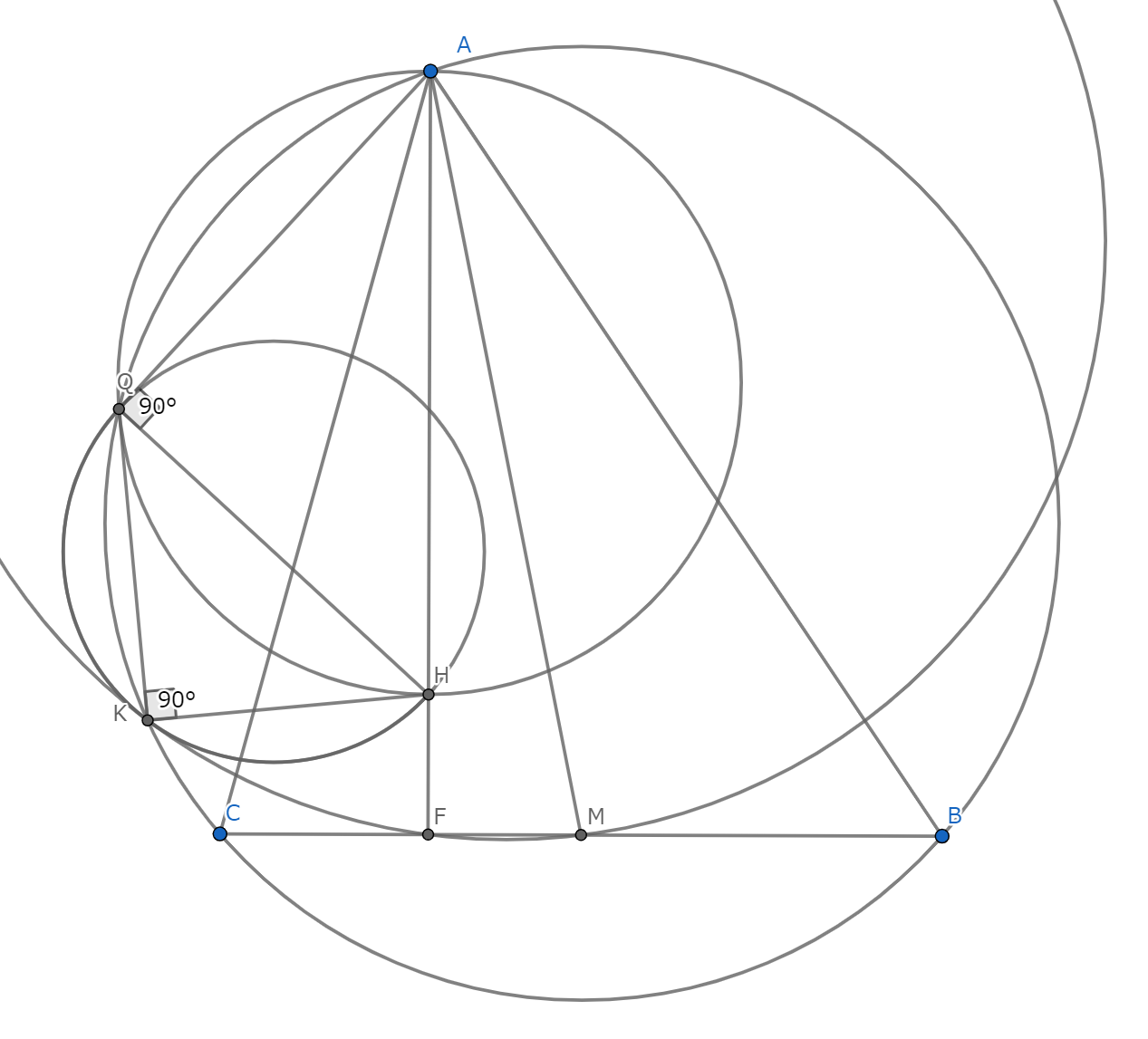IMO2015-3

まず，僕はこれを公式解説とは全く異なった解法で解いたので紹介します．
ネタバレ注意
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓

解答

$A$の$Γ$での対蹠点を$D$とすれば，$\angle HQA=90^{\circ}$より$Q,H,D$は共線であり，有名事実として$H,M,D$は共線なので特に$Q,H,M$は共線．
$M$を中心とする半径$MC$の円による反転$f$を考える．$f$で点$W$が移る先を$W'$と表す．有名事実として$(AQH)$は$f$で不変であり，また$Q,H,M$はこの順に同一直線上にあるので，$(KQH)(=ω$とおく)も$f$で不変である．よって$K,Q,H,K'$は共円．また$B,C,K,Q$は共円なので$B,C,K',Q'$も共円．よって直線$KQ,K'H,BC$は$3$円$(KQHK'),(BCK'Q'),(BCKQ)$の根心($X$とする)で交わる．
さらに，$F',F,Q,H$も共円だから，$\angle F'QM=90^{\circ}$であり，$QH$は$ω$の直径だから，$F'Q$は$ω$に接する．ここで六角形$HQQKK'K'$にPascalの定理を適用すれば，$ω$の$Q$と$K'$における接線の交点，及び点$X$,$M$の$3$点が同一直線上にあることがわかる．したがって$F'K'$は$ω$の接線である．ここで$(KFM)$は$f$で$F'K'$に移り，$ω$は$f$で不変だから，$ω$と$(KFM)$は接する．

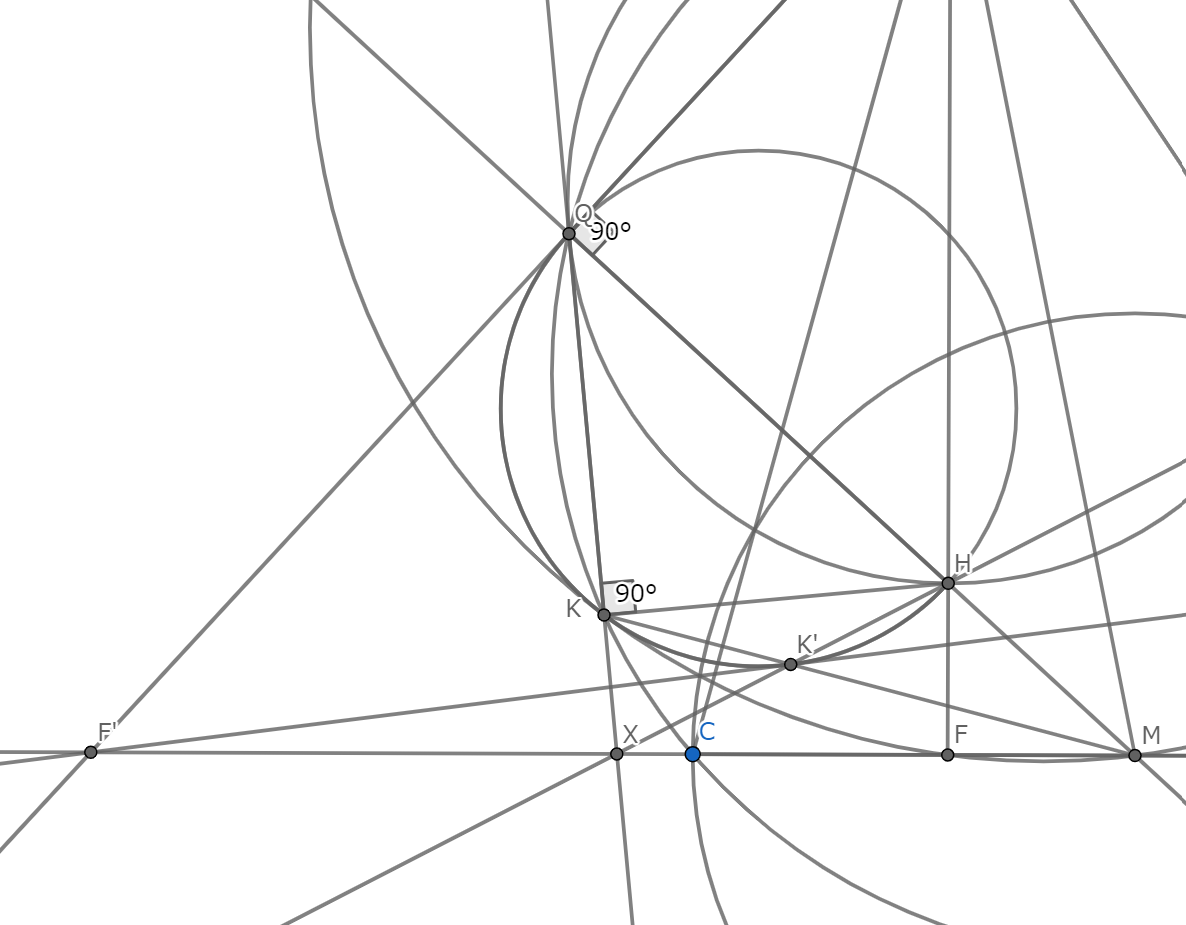反転後
ちなみに，この問題には次のような一般化があるようです．

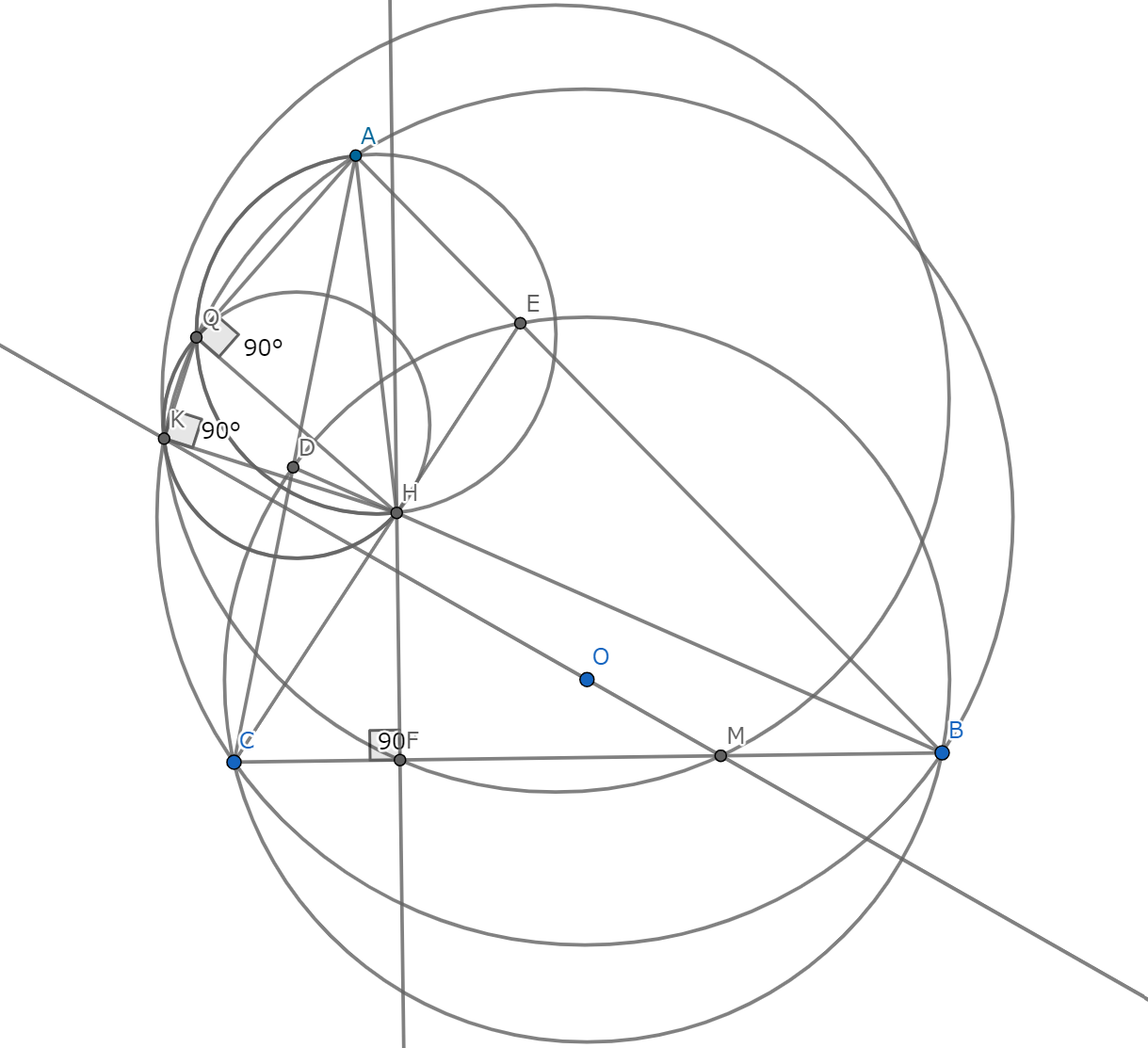IMO2015-3の一般化1

これはAopsの IMO2015-3のページ でLeVietAns氏が投稿していたもの（説明しやすいように一部改題しました）です．これに関しても僕の解法を紹介します．

一般化1への解答

示すべきことは$\angle KQH=\angle HKF+\angle KMF$と言い換えられる．ここで，$KQ$と$BC$の交点を$S$とすると，$\angle SKH=\angle HFS=90^{\circ}$だから$4$点$K,H,F,S$は共円．よって$KM$と$SH$の交点を$T$とすると，$\angle HKF+\angle KMF=\angle HSF+\angle KMF=\angle KTS$だから，$K,Q,H,T$が同一円周上にあることを示せばよい．
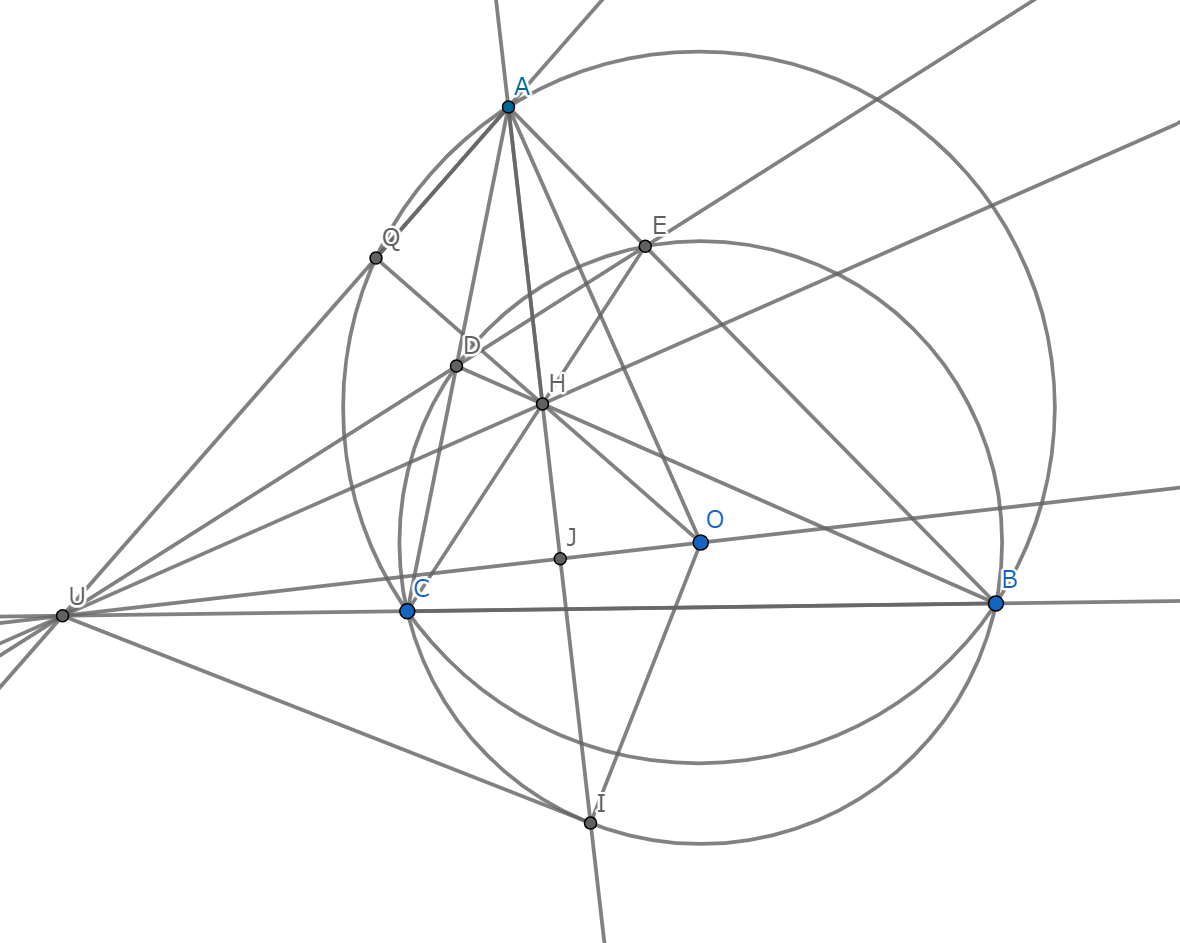一般化1-図1

$DE$と$BC$の交点を$U$，$AU$と$Γ$の交点を$Q'$，$OU$と$(BCDE)$の交点のうち$BC$に関して$A$と異なる側にあるものを$I$とする．Brocardの定理より$H$は三角形$AOU$の垂心であり，$AH$は円$O$に関する$U$の極線である．したがって$\angle UJI=\angle UIO=90^{\circ}$から$\triangle UJI\sim \triangle UIO$となるから，$UI^2=UJ\cdot UO$である．ここで方べきの定理より$UQ'\cdot UA=UC\cdot UB=UI^2$だから$UQ'\cdot UA=UJ\cdot UO$であり，$A,Q',J,O$は同一円周上にある．ゆえに$H$が三角形$AOU$の垂心であることから$O,H,Q'$は共線であり，$\angle AQ'H=90^{\circ}$である．よって$Q=Q'$となる．
$\angle OJI=\angle OIU=90^{\circ}$より$\triangle OJI\sim \triangle OIU$だから$OI^2=OJ\cdot OU=OH\cdot OQ$．したがって$KM$と$(KHQ)$の交点を$T'(\neq K)$とすると，$O$を中心とする半径$OI$の反転によって$Q$は$H$に，$K$は$T'$にうつる．$B,C$はこの反転で不変であり，$B,C,K,Q$は共円だから，$H,T',B,C$は共円である．したがって$3$直線$KQ,T'H,BC$は$3$円$(KQT'H),(T'HBC),(BCKQ)$の根心$S$で交わる．よって$T'=T$であり，$K,Q,H,T$は同一円周上にあることがわかるから，題意は示された．
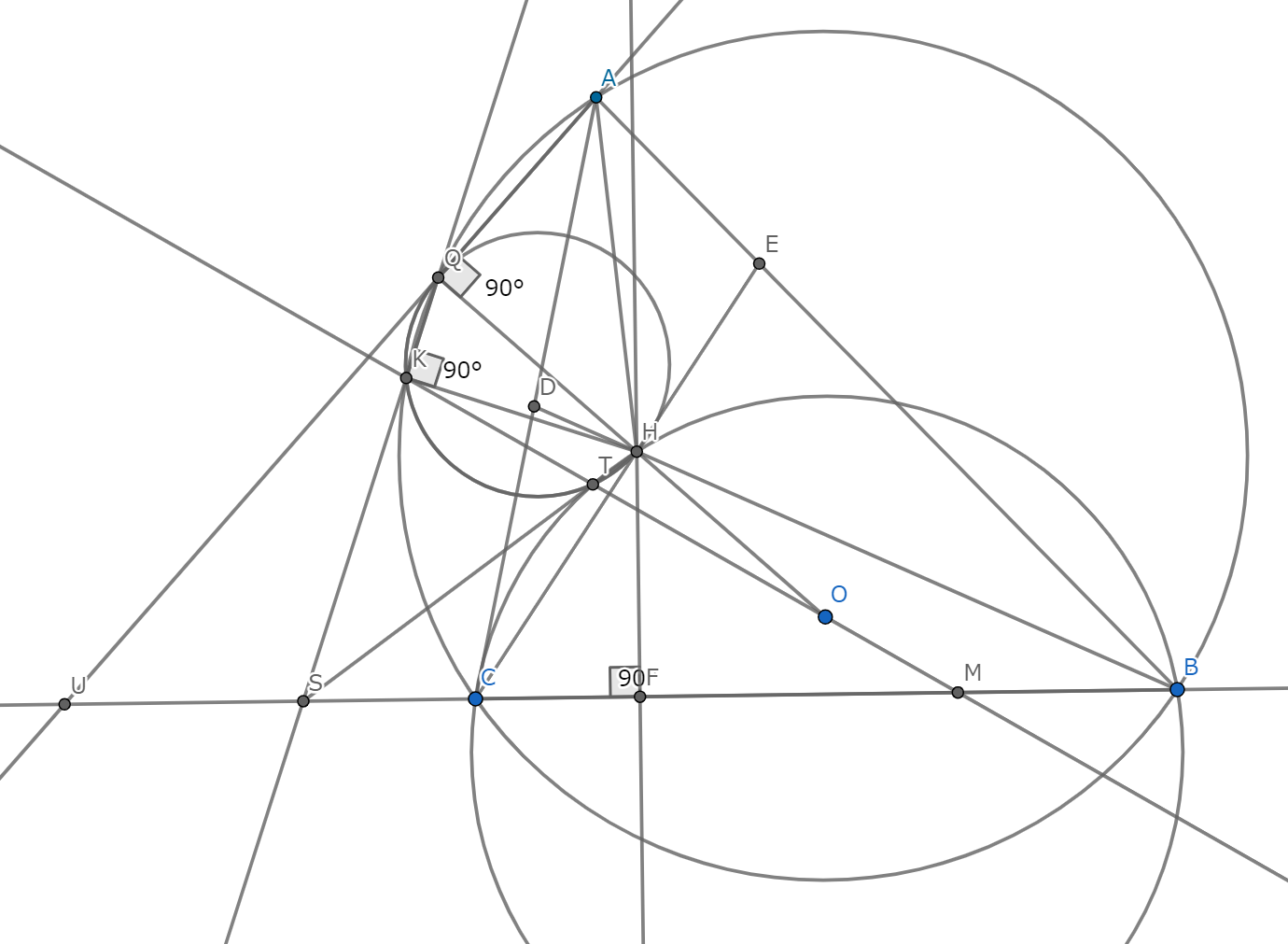一般化1-図2

ちょっと遠回りしてしまったかもしれません．もう少し改良できそうな気がします．
こんな風に問題の一般化が存在すると面白いですよね．他にも，buratinogigle氏による次の一般化が投稿されていました．

これも面白いので興味のある人は考えてみてください．

3.推し問題について

China TST 2019 Test 3 P5

　示すべきことが「～であるような点が取れることを示せ」という珍しい形の幾何です．とっつきにくいかもしれませんが，ちゃんとしたモチベのある（すなわち、やばい天啓とかではない）補助線を引くことできれいに解くことができる大好きな問題です．個人的に$2$番級ぐらいです．

　書いていて気づいたのですが、推し問題の紹介ってネタバレを含まないように良いところを解説していくのが難しいですね…．

EGMO2020 P3

　主張がめちゃくちゃ綺麗ですね．こういった対称性のある六角形幾何（ISL2013G5とか）はハズレがない印象です．条件の言い換えが素晴らしく、とにかく楽しいです．個人的に$2$番級ぐらいです．

JapanTST 2022 P6

　この問題を一言で表すなら，「教育的」でしょう．さまざまな手法がいい感じに詰まっていて，ステップを重ねていくのが楽しい問題です．$2.5$番級といったところだと思います．

China TST 2015 TST2 P3

　初見では点が多すぎてやばいと感じるかもしれませんが，これはChina TST あるある（？）です．接円問題というのは神問であることが多いのですが，これはガチの神問です．複雑な図をきれいに解きほぐしていくのが最高です．$2.8$番級ぐらいだと思います．

終わりに

　ここまで読んでいただきありがとうございました．時間に追われながら無計画にその場で思いついたことを書いたのでハチャメチャな記事になってしまいました．もっと余裕があるときにしっかりとした記事は書いてみたいという気持ちがあります．需要があれば問題の思考過程とかを書きたいですね．この記事が少しでも誰かの役に立てば嬉しいです．
　それでは，良い幾何ライフを！