とある級数の議論
注意
今回は、以下の級数の証明に関する議論の記事ではありません。
初めに
こんにちは。Arsenicです^^
まぁ級数します。
今回は、とある級数がいつものように友達から送り付けられたので、いつも通りいつも通りしました。
さらに、今回は、証明した後に友達から変なものが送り付けられたので、それを主に紹介いたします(上の注意はこのことです..)
そんな級数(どんな級数)
以下です。
任意の$p>0$に対し、
$$\sum_{n=2}^{\infty} \left(1- \sum_{n=1}^{\infty} \dfrac{(-1)^n}{(pn+1)^k} \right)$$ってどうなるの???????????????
元の問題は、
$$\sum_{n=2}^{\infty} \left( 1-\beta(n)\right)=\dfrac{1}{4} (\pi+\log 4-4)$$
です
僕が馬鹿なことは認めるんですケドさすがに舐められすぎですね～
見た瞬(=見た瞬間)で下の2つが思いつきます^^
$$\beta(k)=\sum_{n=0}^{\infty} \dfrac{(-1)^n}{(2n+1)^k}$$
$G=\beta(2)$
今回、Catalan constantになるのは、$k=2$の場合ですね；
でもなんですよにぇ～～～
使わないんですよにぇ～～～
これを使って悩んだ挙句同じようなことをループしてた阿保が僕です!
議論
ここからです。
下のように言い換えることができる。
$$\sum_{k=2}^{\infty} \left[ 1- \sum_{n=0}^{\infty} \dfrac{(-1)^n}{(pn+1)^k} \right]=\sum_{k=2}^{\infty} \sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{(pn+1)^k}$$
$$=\sum_{n=1}^{\infty} (-1)^{n-1} \sum_{k=2}^{\infty} \dfrac{1}{(pn+1)^k}$$
$$=\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{(pn+1)^2} \sum_{k=0}^{\infty} \dfrac{1}{(pn+1)^k}$$
そして、
$$\sum_{k=0}^{\infty} \dfrac{1}{(pn+1)^k}=\dfrac{1}{1-\frac{1}{pn+1}}=\dfrac{pn+1}{pn} \cdots ①$$とおくと、
先ほどの級数は、
$$\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{pn(pn+1)} \mathrm{(since ①)}$$
ここで、$p=2$を代入すると、先ほどの式と一致する。
っていうかんじですね～。
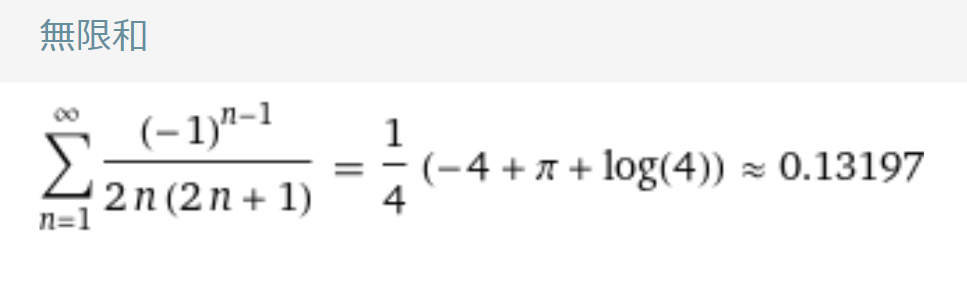結果(参考までに)
議論の続き
続きがあります。
BBB(部分分数分解)を用いると、
$$\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{pn(pn+1)}=\sum_{n=1}^{\infty} (-1)^{n-1} \left( \dfrac{1}{pn}-\dfrac{1}{pn+1}\right)$$
$$=\dfrac{\log 2}{p}-\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{pn+1}$$
$p \in \mathbb{Z}$であり、$\zeta_p$で、$p$番目の$1$の根であるとする。この時、
$$\dfrac{\log(1+z)}{z}+\dfrac{\log (1+\zeta_p z)}{\zeta_{p} z}+ \cdots \dfrac{\log (1+\zeta_p ^{p-1} z)}{\zeta_p ^{p-1} z}$$
$$=\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n}z^{n-1} \sum_{k=0}^{p-1} \zeta_p ^{k(n-1)}$$
$$=\sum_{n=1}^{\infty} \dfrac{(-1)^{n-k}}{pn+1}z^{pn}$$
$z=1$とおくと、次の等式を導出できる。
$$\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{pn+1}=\sum_{k=0}^{\infty} \dfrac{\log (1+\zeta_p ^k)}{\zeta_p ^k z}$$
したがって、一番最初の級数は、
$$\dfrac{1}{p} \log 2+\sum_{k=0}^{p-1} \dfrac{\log(1+\zeta_p ^k)}{\zeta_p ^k z}$$
ラスト(締め)
実はもう一つあるんですがそれは機会があったらですね～。
everyoneの感想
A:huh?
U:きれいに収まったなぁ～
T:へ～
F:ふ～ん
M:わわわわわ
↑(A,U,T,F,M)議論メンバー
蛇足
最近の記事の内容はとても薄いですね。
反省します。
ほかの考え方や世紀の大誤植などがあったらご一報ください。著者が暇なとき対応します
この記事の編集時間:30分強
文字数(TeXコード含):知らん
編集者:Arsenic(だいぶTeX打ち慣れてきた)
はぁぁぁぁいぃぃぃぃおわりぃぃぃ!!!
MEMO
2024/03/23/13:17 指摘の誤植を訂正
2024/04/01/15:07 著者発見の誤植を訂正