正四面体の性質

はじめに

長さ、体積など基本的な正四面体の量を簡単にまとめてみた。
そのうち、証明や図を追加するかも。

設定

立方体の上面にある正方形の頂点の一つを$\mathrm{A}$とする。
頂点$\mathrm{A}$から反時計回りに、正方形の他の頂点を$\mathrm{B}$,$\mathrm{C}$,$\mathrm{D}$とする。
立方体の外心を点$\mathrm{O}$とする。
点$\mathrm{O}$に関して点$\mathrm{A}$と対称の位置にある頂点を$\mathrm{A}'$とする。
同様に頂点$\mathrm{B}'$,$\mathrm{C}'$,$\mathrm{D}'$を定める。
このとき四面体$\mathrm{AC}\mathrm{B}'\mathrm{D}'$は正四面体となる。

四面体$\mathrm{AC}\mathrm{B}'\mathrm{D}'$において、頂点$\mathrm{A}$から面$\mathrm{C}\mathrm{B}'\mathrm{D}'$に垂らした垂線の足を点$\mathrm{H}$とする。
さらに、線分$\mathrm{A}'\mathrm{C}'$の中点を$\mathrm{X}$とする。

また、以下のように文字を定める。

$l$：立方体の一辺の長さ
$a$：正四面体の一辺の長さ
$R$：正四面体の外接円の半径
$r$：正四面体の内接円の半径
$h$：正四面体の高さ
$e$：$\mathrm{HA}'$の長さ
$\theta$：正四面体の中心角。$\angle\mathrm{AOC}$
$\alpha$：正四面体の2つの面がなす角。$\angle\mathrm{AXC}$
$h_{\triangle}$：正四面体の底面（正三角形）の高さ
$S_{\triangle}$：正四面体の底面（正三角形）の面積
$R_{\triangle}$：正四面体の底面（正三角形）の外接円の半径
$r_{\triangle}$：正四面体の底面（正三角形）の内接円の半径
$V_\mathrm{C}$：立方体の体積
$V_\mathrm{T}$：正四面体の体積
$V_\mathrm{P}$：頂点四面体（四面体$\mathrm{ABCD'}$）の体積

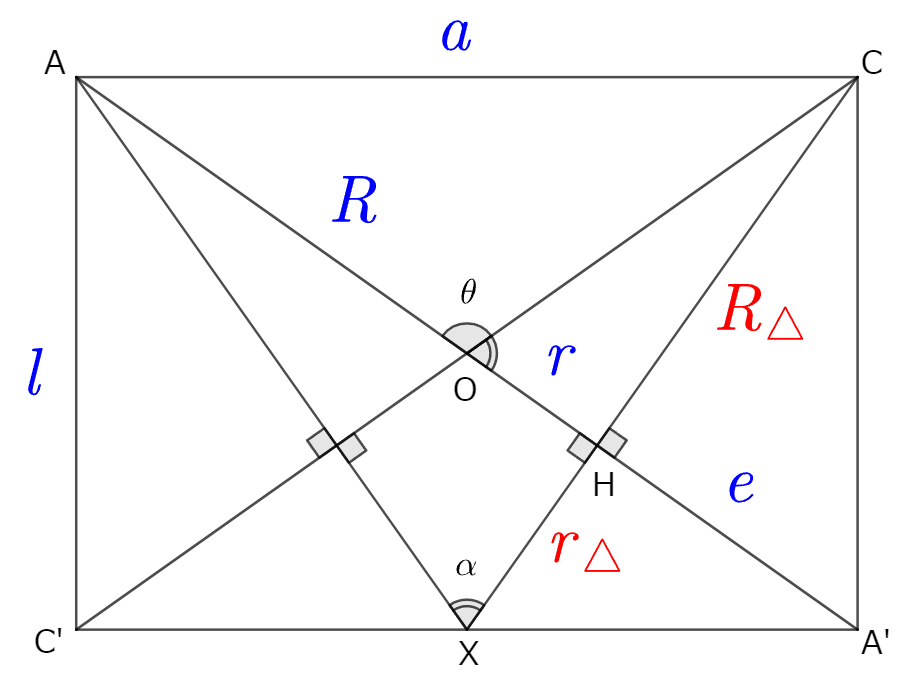断面図

計量

$$a=\sqrt{2}l$$
$$l=\frac{\sqrt{2}}{2}a $$

$$V_\mathrm{C}=l^3=\frac{\sqrt{2}}{4}a^3$$
$$V_\mathrm{P}=\frac{l^3}{6}=\frac{\sqrt{2}}{24}a^3$$
$$V_\mathrm{T}=\frac{1}{3}l^3=\frac{\sqrt{2}}{12}a^3$$

$$r=\frac{\sqrt{3}}{6}l=\frac{\sqrt{6}}{12}a $$
$$e=\frac{\sqrt{3}}{3}l=\frac{\sqrt{6}}{6}a $$
$$R=\frac{\sqrt{3}}{2}l=\frac{\sqrt{6}}{4}a $$
$$h=\frac{2\sqrt{3}}{3}l=\frac{\sqrt{6}}{3}a $$
$$R+r=h$$

この$\theta$ をマラルディの角度というらしい。

$$h_{\triangle}=\frac{\sqrt{3}}{2}a=\frac{\sqrt{6}}{2}l$$
$$S_{\triangle}=\frac{1}{2}ah_{\triangle}=\frac{\sqrt{3}}{4}a^2=\frac{\sqrt{3}}{2}l^3$$
$$R_{\triangle}=\frac{2\sqrt{2}}{3}R=\frac{\sqrt{6}}{3}l=\frac{\sqrt{3}}{3}a $$
$$R_{\triangle}+r_{\triangle}=h_{\triangle}$$

おわりに

正四面体の重要な長さ（比）や角度は、A4（$1:\sqrt{2}$）の紙を使えば大体再現できる
という気付きを得た。
今まで白銀比にはあまり面白味を感じてなかったけど、触ってみたら結構面白かった印象。