台形の面積の公式を直観的に理解する

こんにちは。台形の面積の公式ってわかりにくいですよね。

$ \text{面積} = (\text{上底} + \text{下底}) \times \text{高さ} ÷ 2 $

台形

この記事では、私がこの公式をどう理解しているかを紹介します。

紹介

まず、台形を反時計回りに$ \frac{1}{4} $回転させて、カヴァリエリの原理を適用すると、次のような形に変形できます。ここで、$ \angle CDA = \angle BAD = 90\degree $です。

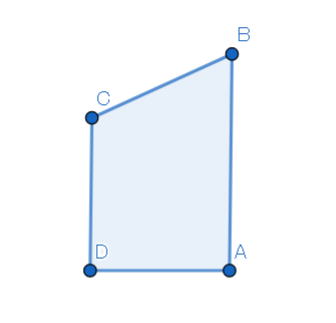台形を変形させる

さて、突然ですが$ BC $の中点が原点となるように座標を入れます。

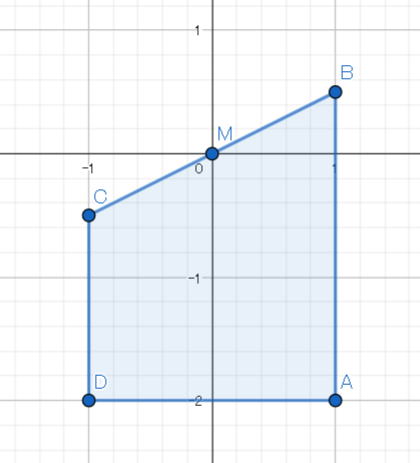台形に座標を入れる

$ D(-s, -t) $とし、直線$ CB $の方程式を$ y=f(x) $とすると、台形の面積$ S $は次で表されます:

\begin{align*} S &= \int_{-s}^{s} (f(x) - (-t)) dx \\ &= \int_{-s}^{s} f(x) dx + \int_{-s}^{s} t dx \\ &= \int_{-s}^{s} f(x) dx + t(s - (-s)) \\ \end{align*}

ここで、$ f(x) $は奇関数なので(そうなるように原点を調整しました)、最後の式の積分の部分は$ 0 $になり、また一次関数の性質から$ t = \frac{AB + CD}{2} $が成り立つので、

\begin{equation*} S = t(s - (-s)) = \frac{AB + CD}{2} \cdot AD \end{equation*}

が成り立ち、台形の面積の公式と同じものを得ることができました。

余談

私の記事でときどき台形の面積を求める式が出てくることがありますが、÷2が真ん中に来ているのはこれが理由です。