「コラッツ予想」の視覚化と確率的な考察

本稿では「コラッツ予想」に関する新たな視覚化の方法（「コラッツ・マップ」と名付ける）を提示する。このコラッツ・マップを使えば、コラッツ予想の数々の特徴が視覚的に理解できることになる。

さらに、このマップから導出される分布を踏まえて確率的に考えると、コラッツ予想が成り立つことも示すことができる。

第1章 初めに

本稿では「コラッツ予想（※）」に関する新たな視覚化の方法として「コラッツ・マップ」というものを提示する。そして、このコラッツ・マップを使って確率的に考えると、コラッツ予想が成立することが強く期待できることを示す。

※）「コラッツ予想」とは以下の予想のことである。 任意の正の整数$n$に対して、以下の操作を考える。
　・${n}$が奇数の場合、${n}$を3倍して1を足す
　・${n}$が偶数の場合、${n}$を2で割れなくなるまで割る
このとき、「どんな初期値から始めても、有限回の操作のうちに必ず1に到達する」という主張が「コラッツ予想」である。

本稿では、上記操作を行って一連の数列を得ることを「コラッツ展開」と呼ぶことにする。コラッツ展開は以下のように表すことができる。なお、本質的に奇数部分のみを考えれば良いので、特に断りのない限り、コラッツ展開は偶数部分を省いた数列のみを記述するものとする。
　①初期値 5： 5→16→1
　②初期値13： 13→40→5→16→1
　③初期値21： 21→64→1

第2章 準備

本稿では以下のような表を頻繁に使うので、準備段階として、まずはこの表の見方について説明する。

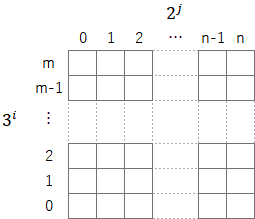
この表の各セル${a_{i,j} (i=0,\cdots,m;j=0,\cdots,n)}$には数字が一つ入り、全体で以下のような集計値${S}$を構成する。

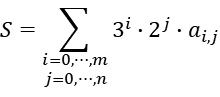
表に入る数字は特に限定しないが、本稿では次のように基本的に0、±1を入れて使用する（見やすさのため、特に断らない限りゼロの表記は省略して空白とする）。

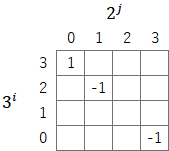
上記の表では、${a_{3,0}=1, a_{1,1}=-1, a_{0,3}=-1}$だけに数字が入り、その他はゼロが入っている（ゼロの表記は省略している）。そのため、この表の集計値${S}$を計算すると以下のように${13}$となる。
$${S=3^3 \cdot 2^0 \cdot a_{3,0}+3^1 \cdot 2^1 \cdot a_{1,1}+3^0 \cdot 2^3 \cdot a_{0,3}=13}$$

この表は二進数や三進数の拡張になっていると言える。たとえば、十進法の${(35)_{10}}$は、二進法では${(100011)_{2}}$、三進法では${(1012)_{3}}$と表現されるが、この表では以下のように表現される（二進法表記とは並び順が逆になっていることは注意されたい）。

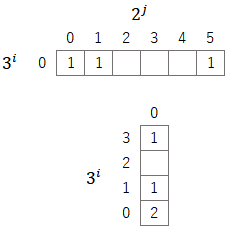
また、二進法や三進法では数字の並びは一意に定まるが、この表では同じ集計値でも異なる表現が可能である。たとえば、十進法の${(27)_{10}}$ は以下のように様々な形で表現できる。この性質はこの先の議論で重要になってくる。

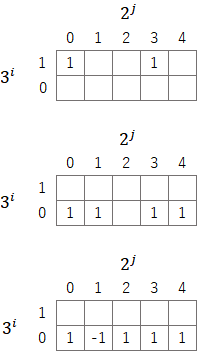
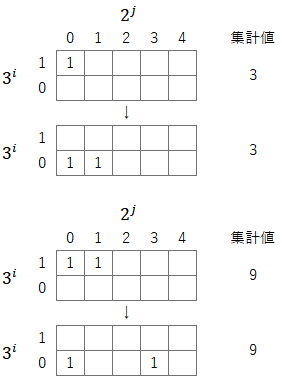
なお、上記の例でも分かるが、この表で集計値が変わらないように数字を下に移動させると、以下のように3倍（二進法表記では${(11)_2}$倍）になる。この特性もこの先の議論で重要になってくるので、認識しておいてほしい。

第3章 コラッツ展開を視覚化する操作

さて、これで準備が整った。この表を使うことでコラッツ展開を視覚化することができる。まず本章では初期値「13」を例にして、コラッツ展開を視覚化するための具体的な操作について説明する。

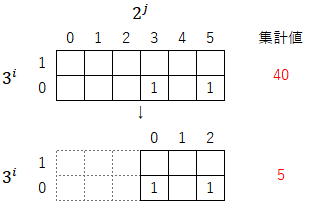
操作①「3倍して１を足す」：表を下に拡張して${3^i}$の指数を振り直す。この操作により集計値は「3倍して１を足す」値になる。

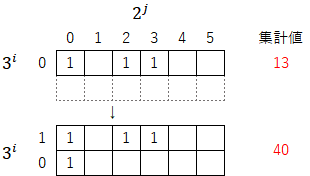
操作②「上方の数列を最下行に移動させる」：数列を移動させるだけなので、この操作では集計値は変わらない（逆に「集計値が変わらないように数列を下行に移動させている」とも言える）。

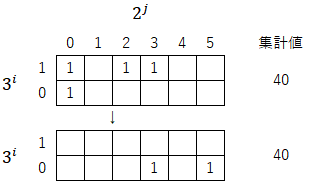
操作③「2で割れるだけ割る」：最小の位が「1」になる位置まで列の起点を移動して${2^j}$の指数を振り直す。この操作により集計値が「2で割り切った」値になる。

第4章 コラッツ展開の視覚化

上記の操作①～③を繰り返すことでコラッツ展開を視覚化することができる。本章では「初期値17」を例にして、コラッツ展開がどのように視覚化できるかを説明する。

0）まず初期値17を設定する。当然だが、集計値は「17」となる。

1-1）3倍して１を足す（操作①）。すると、集計値は「${17\cdot3+1=52}$」となる。

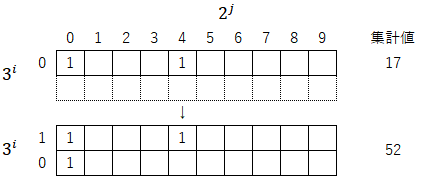
1-2）上方の数列を最下行に移動させる（操作②）。この操作では集計値は変わらない。

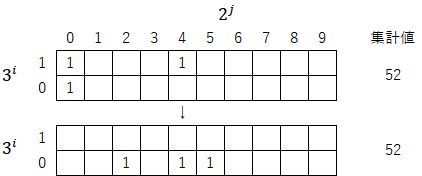
1-3）最小の位が「1」になる位置まで列の起点を移動して指数を振り直す（操作③）。この操作で集計値は「${52÷2^2=13}$」となる。

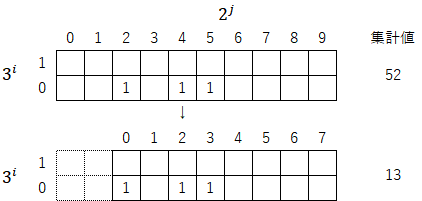
2-1）同様の操作を繰り返す。まず3倍して１を足す（操作①）。ここで集計値は「${13\cdot3+1=40}$」となる。

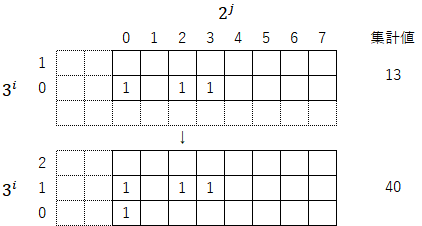
2-2）上方の数列を最下行に移動させる（操作②）。この操作では集計値は変わらない。

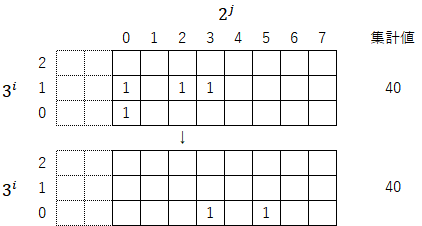
2-3）最小の位が「1」になる位置まで列の起点を移動して指数を振り直す（操作③）。この操作で集計値は「${40÷2^3=5}$」となる。

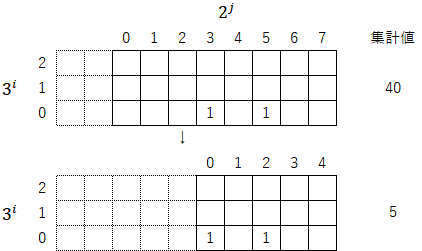
3-1）再び、3倍して１を足す（操作①）。この操作で集計値は「${5\cdot3+1=16}$」となる。

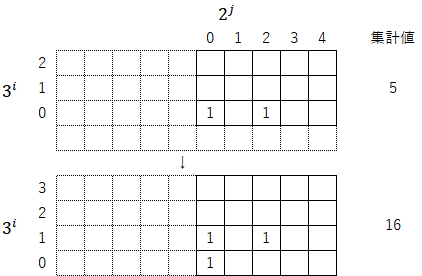
3-2）上方の数列を最下行に移動させる（操作②）。この操作では集計値は変わらない。

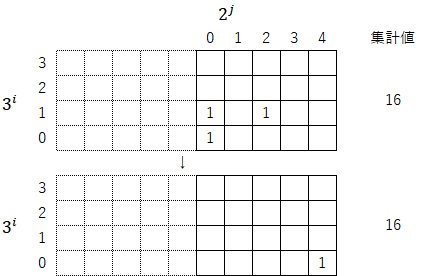
3-3）最小の位が「1」になる位置まで列の起点を移動して指数を振り直す（操作③）。集計値は「${16÷2^4=1}$」となる。

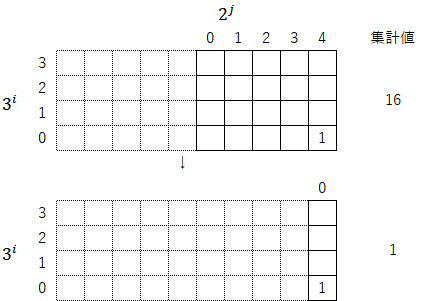
4）集計値が「1」となった時点で、全操作を終了させる。

このように、操作①～③を繰り返すことで、コラッツ展開を視覚化することができる

第5章 コラッツ・マップ

ここで、表を見やすくするためにさらにもう一つ工夫を加える。「3倍して1を足す」操作を行うときの「1を加える」場所にマークを付ける（本稿ではセルを黄色に塗る）。そして、それ以外の「1」のマスにも別のマークを付ける（本稿ではセルをオレンジ色に塗る）。

先ほどの展開図（初期値17）を例に取ると、以下のようになる。

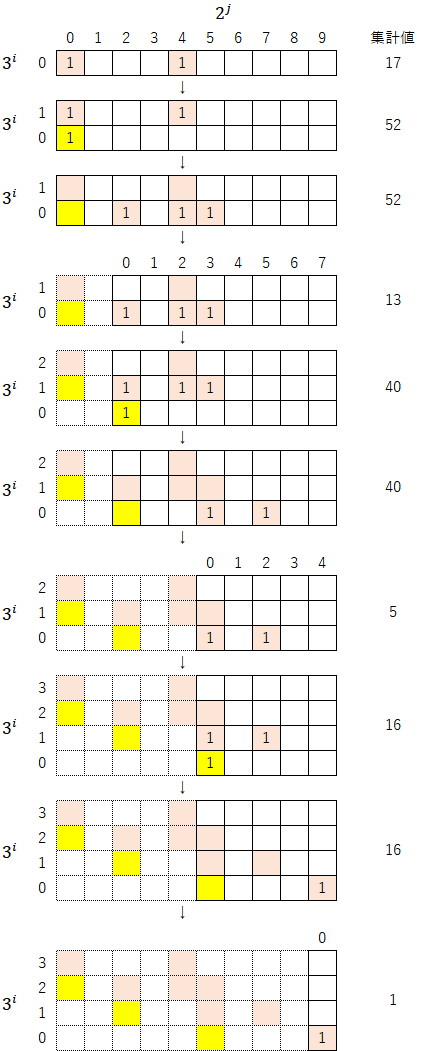
このようなマークを付けることで、ある初期値がどのような経過を経て最終的に1に収束したのかを視覚的に理解することができる。本稿では、このように色付けした表を「コラッツ・マップ（あるいは省略して単に『マップ』）」と呼ぶことにする。

参考までに、いくつかの初期値とそこから始まるマップを以下に示す。計算してもらえば分かるが、各ステップの集計値はコラッツ展開の値と同じになる。また、初期値とマップが1対1に対応していることは言うまでもないと思う。

①初期値5（5→16→1）

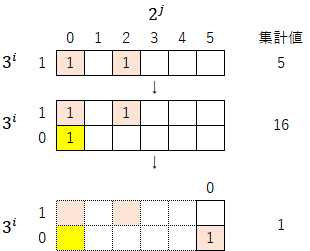
②初期値13（13→40→5→16→1）

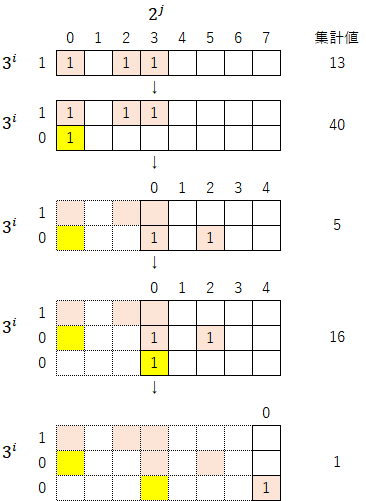
③初期値21（21→64→1）

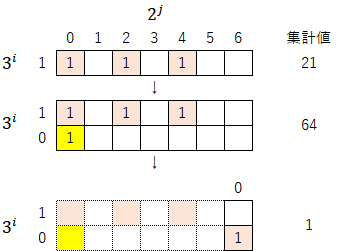
④初期値31このコラッツ展開は以下のように非常に長くなるので、マップもかなり大きくなる（初期値31のマップが大きくなる理由については、後ほど別の章で取り上げてみたい）。31→47→71→107→161→121→91→137→103→155→233→175→263→395→593→445→167→251→377→283→425→319→479→719→1079→1619→2429→911→1367→2051→3077→577→433→325→61→23→35→53→5→1

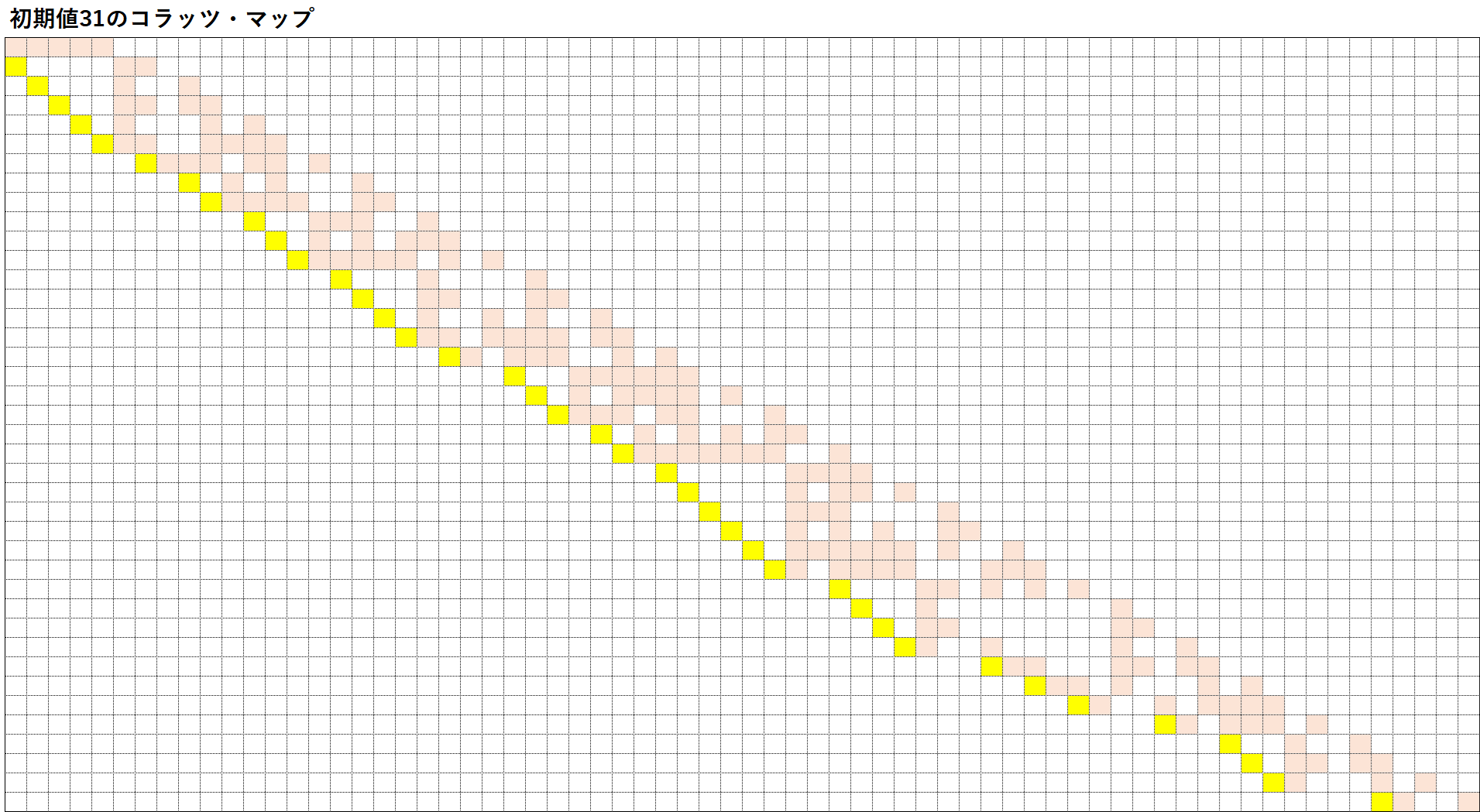
第6章 コラッツ・マップの求め方

本章では「ある初期値に対応するコラッツ・マップの求め方」について説明する。途中の段階をあまり省略せずに説明しているため、少し長くなっているが、ご了承いただきたい。なお、必要に応じて途中で端折っていただいても構わない。また、先ほどの操作①～③と似ているところもあるが、微妙に異なる点もあるので注意されたい。

なお、本章では「初期値29」を例として取り上げるが、他の初期値でも基本的な考え方は同じである。

0-0）まず、初期値29を設定する。

0-1）続いて最左列の「1」を「-1」に置き換える。そして、集計値が変わらないように他の数字にも修正を加える。なお、「-1」が新たに出てきたので、今後はそこに緑色マークを付けていく。

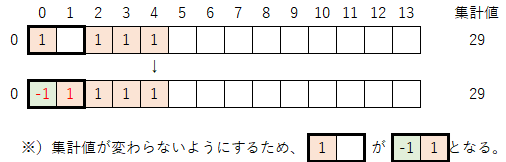
0-2）「-1」と「1」の並びに注目し、以下のルールに従って、表を下に拡張させて指数を振り直す。

①「-1」と「1」が隣り合っている場合は、表を１行だけ下に拡張させる。

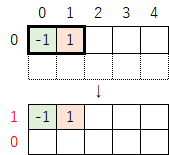
②「-1」と「1」の間が何マスか空いている場合は、その空いているマスの分だけ行を下に拡張させる。なお、隣り合っている場合でも1行だけ拡張させるので、以下の例のように2マス空いている場合は（2+1で）３行拡張させることになる。

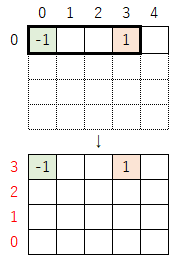
今回の例（初期値29）では「-1」と「1」が隣り合っているので、１行だけ拡張させて指数を振り直す。この操作により、集計値は「29→87」へと変化する。

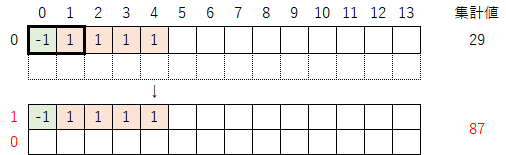
0-3）拡張した行に黄色マークを付ける。ここでは以下のルールに従って色を付けていく。

①１行だけ拡張した場合は「-1」マスの真下にだけ黄色マークを付ける。

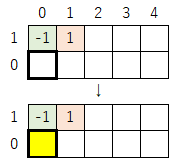
②２行以上拡張した場合は、最初に「-1」マスの真下にだけ黄色マークを付け、その後は斜め下に伸びるように黄色マークを付けていく。

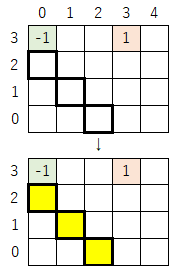
今回の例（初期値29）では拡張した行が１行なので、単純に「-1」マスの真下にだけ黄色マークを付ける。

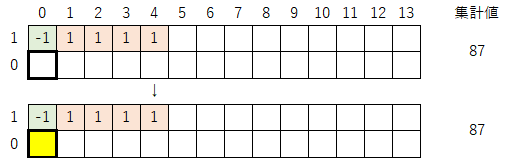
1-0）同様の操作を行っていく。まず、緑色マークの右側にある数列（太枠で囲まれた部分）を、集計値が変わらないように最下行に移動させる。

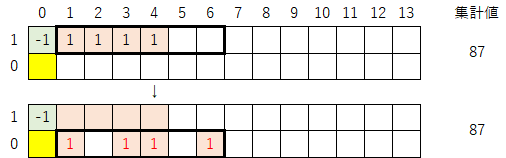
1-1）次に、最下行の数列を変形する。ただし、今度は左から2番目の「1」を「-1」に置き換える。そして、先ほどと同様に、集計値が変わらないように他の数字も修正を加える。

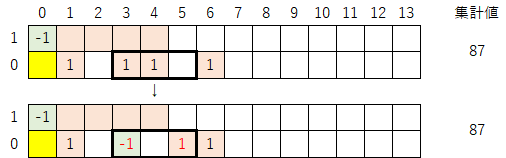
1-2）表を下に拡張し指数を振り直す。拡張する行数は「-1」と「1」の間隔なので、今回は２行拡張させる。この操作により、集計値は「87→783」へと変化する。

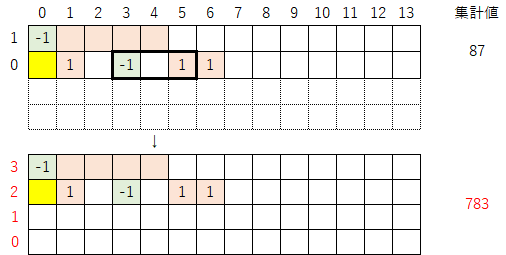
1-3）拡張した行に黄色マークを付ける。今回は拡張した行が２行なので以下のように斜めに黄色マークを付けていく。

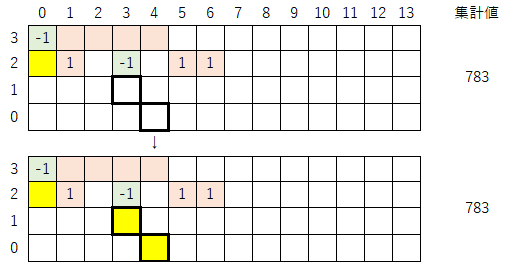
2-0）緑色マークの右側にある数列（太枠で囲まれた部分）を、集計値が変わらないように最下行まで移動させる。今回の例では２行移動させることになる。

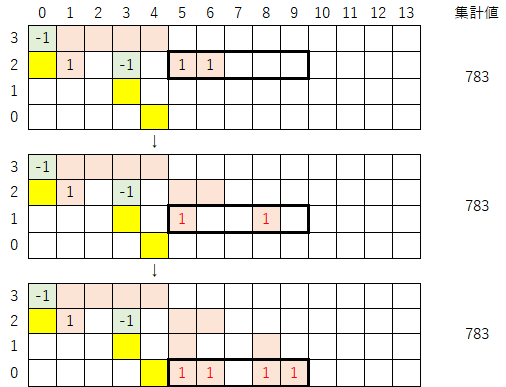
2-1）同様の操作を繰り返す。まず、最下行の左から2番目の「1」を「-1」に置き換える。そして、集計値が変わらないように他の数字も修正を加える。

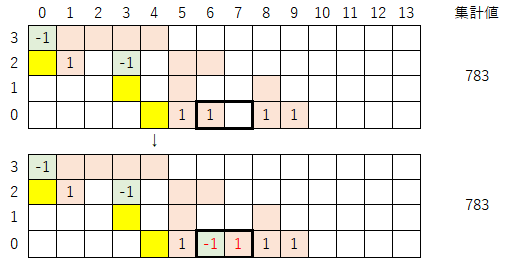
2-2）続いて、表を下に拡張し指数を振り直す。拡張する行数は「-1」と「1」の間隔なので、今回は1行拡張させる。この操作により、集計値は「783→2349」へと変化する。

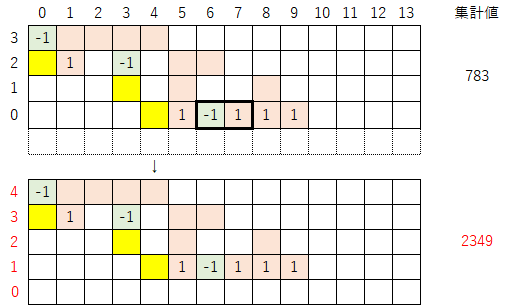
2-3）拡張した行に黄色マークを付ける。今回は拡張した行が１行なので、単純に「-1」があるマスの真下に黄色マークを付ける。

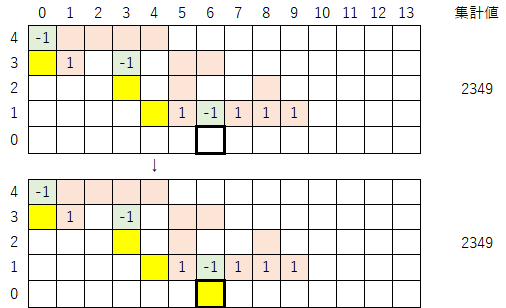
（※以降、同様の手順を繰り返すだけなので、読み飛ばしてもらっても構わない）

3-0）黄色マークの右側にある数列（太枠で囲まれた部分）を、集計値が変わらないように最下行まで移動させる。今回の例では1行移動させることになる。

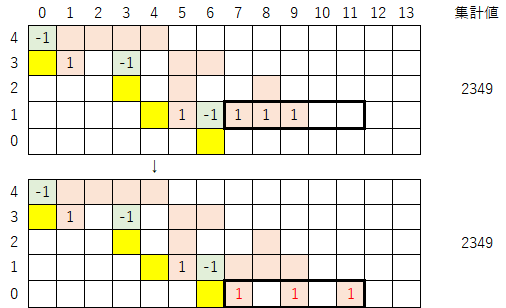
3-1）再び、最下行の左から2番目の「1」を「-1」に置き換える。そして、集計値が変わらないように他の数字も修正を加える。

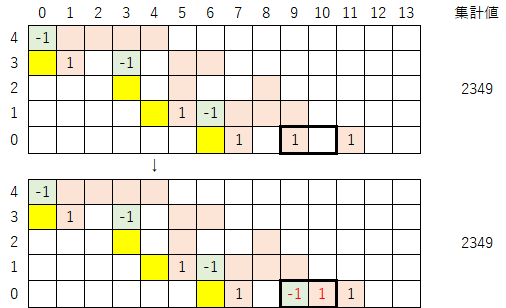
3-2）表を下に拡張し指数を振り直す。拡張する行数は「-1」と「1」の間隔なので、今回は1行拡張させる。この操作により、集計値は「2349→7047」へと変化する。

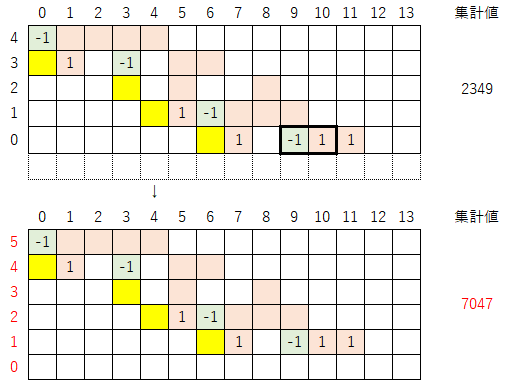
3-3）拡張した行に黄色マークを付ける。今回は拡張した行が１行なので、単純に「-1」があるマスの真下に黄色マークを付ける。

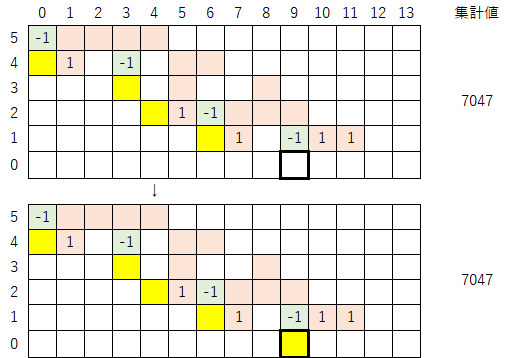
4-0）黄色マークの右側にある数列（太枠で囲まれた部分）を、集計値が変わらないように最下行まで移動させる。今回は1行移動させることになる。

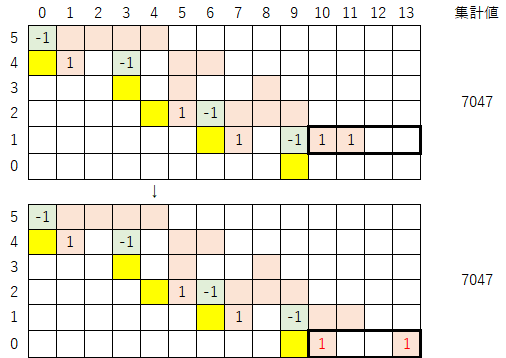
4-1）最終的に、最下行の（黄色マークを除く）数列が以下のように「両側が1、間が全て0」となった時点で操作を終了とする。

4-2）このようにして「初期値29」のコラッツ・マップを作成することができた（見やすさのため数字は記載しないでおく）。

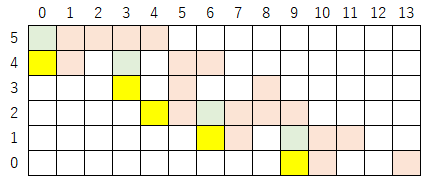
いかがだろうか。最初は複雑そうに見えて若干戸惑うかもしれないが、個々の操作自体は機械的な単純作業であるので、慣れてしまえばそれほど難しくないと思う。

第7章 「マップ＝視覚化」の確認①

さて、このマップが実際に、初期値29のコラッツ展開（29 → 88 → 11 → 34 → 17 → 52 → 13 → 40 → 5 → 16 → 1）を表しているかは、以下のように集計値を見れば確認することができる。

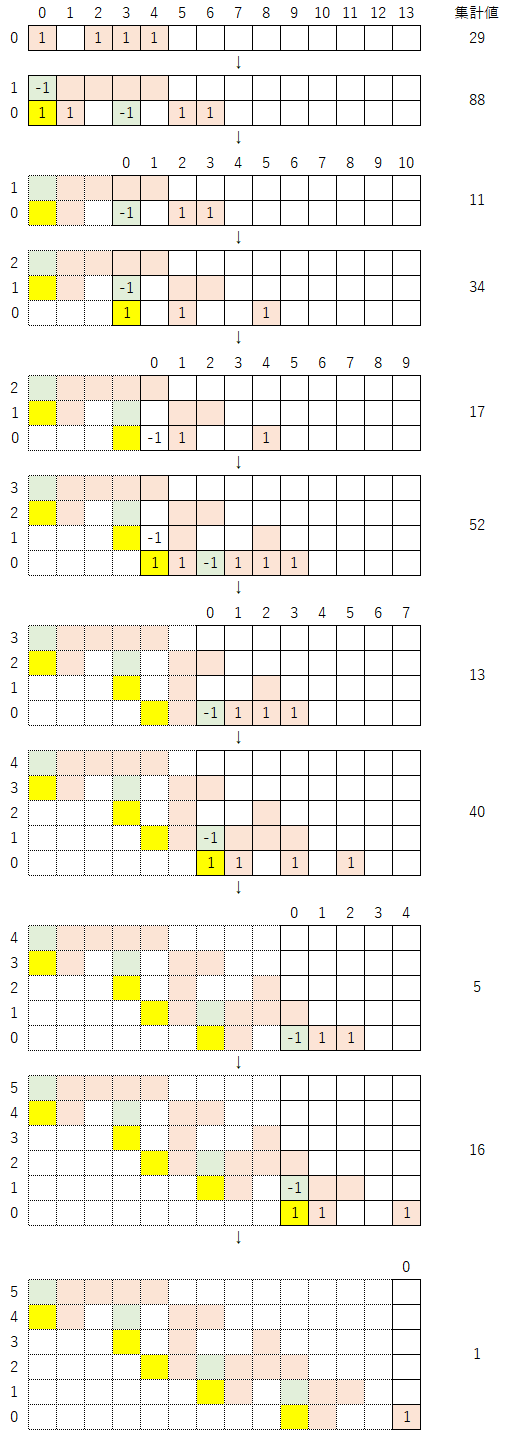
なお、このコラッツ展開（29 → 88 → 11 → 34 → 17 → 52 → 13 → 40 → 5 → 16 → 1）のうち、奇数部分だけを取り出したもの（29 → 11 → 17 → 13 → 5 → 1）は以下のようになり、このように表示した方が分かりやすいかもしれない。

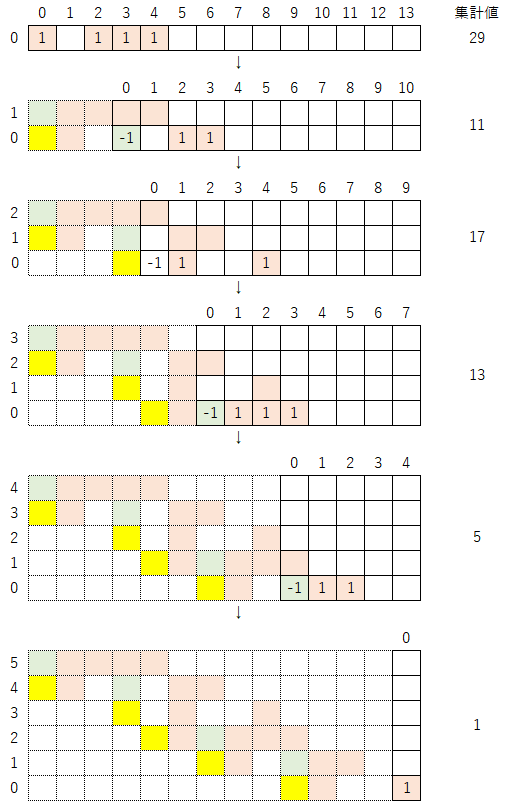
第8章 「マップ＝視覚化」の確認②

このマップがコラッツ展開を視覚化していることは、別の視点からも確認することができる。

「初期値29」のコラッツ・マップの作製過程を再度記載する。

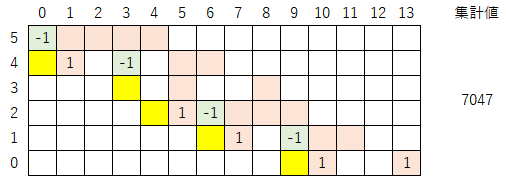
ここから、見やすさのため、オレンジ色と緑色のマークを省くと以下のようになる。

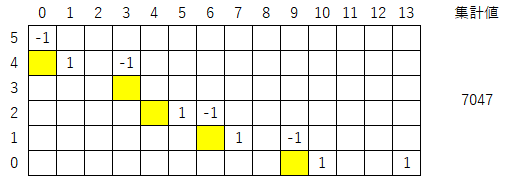
このマップの集計値は「7047」だが、これは初期値「29」と次のような関係になる。
$${7047=29\cdot3^5}$$

つまり、これは以下の二つのマップが「同じ集計値を持つ」ことを意味する（集計値を変えないように変形しているので当たり前だが）。

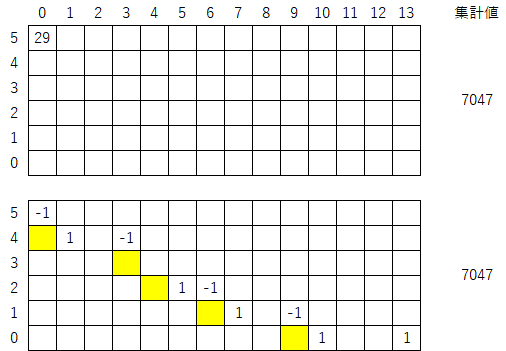
さて、ここで黄色マークに本来記入されるべき「1」を加え、以下のように囲ってみる。

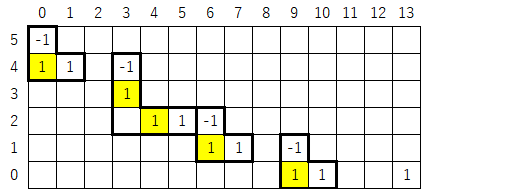
すると、各々の囲みの集計値はいずれもゼロとなり、右下の「1」だけが残ることが分かる。つまり、このマップに沿った形で計算を繰り返していけば、最終的に右下の「1」のみが残り、このマップがコラッツ展開の視覚化を体現していることが分かる。

第9章 コラッツ・マップの漸化式

これまでの説明で、コラッツ・マップについて大分理解いただけたと思う。ここから先の章では、コラッツ・マップを基にした漸化式について論じていく。なお、引き続き、初期値29のマップを例にとって説明する。

まず、初期値を$b_0$とする（後の整合性のため$b_0$を用いる）。$b_0$は以下のように示される。

 
そして、このb_0から「-1」部分を外した数列（太枠で囲った部分）を$c_0$と定義する（このとき指数も振り直す）。

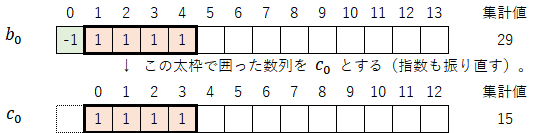
このように定義すると、変数（$b_0$,$c_0$）は以下の関係式で表すことができる。
$${b_0=29}$$
$${c_0=(b_0+1)\cdot\left(\frac{1}{2}\right)^1=15}$$

次に、一行拡張したマップを考える。

この最下行に対して、以下のような変数（$a_1$,$b_1$,$c_1$）を定義する。

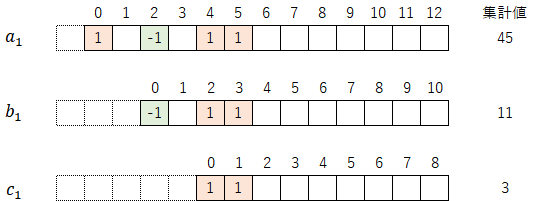
これらの変数（$a_1$,$b_1$,$c_1$）をひとつにまとめると以下のような関係となる。

このとき、変数（$a_1$,$b_1$,$c_1$）は以下の関係式で表すことができる。
$${a_1=c_0\cdot3^1=45}$$
$${b_1=(a_1-1)\cdot\left(\frac{1}{2}\right)^2=11}$$
$${c_1=(b_1+1)\cdot\left(\frac{1}{2}\right)^2=3}$$
 
同様にマップの行を拡張していく。

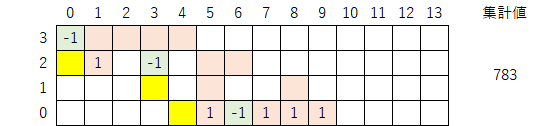
先ほどと同じく、以下のような変数（$a_2$,$b_2$,$c_2$）を定義する。

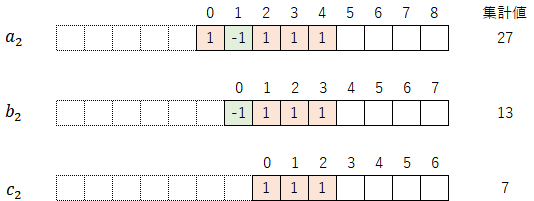
先ほどと同様に、変数（$a_2$,$b_2$,$c_2$）は以下の関係式で表すことができる。
$${a_2=c_1\cdot3^2=27}$$
$${b_2=(a_2-1)\cdot\left(\frac{1}{2}\right)^1=13}$$
$${c_2=(b_2+1)\cdot\left(\frac{1}{2}\right)^1=7}$$

以下、同様の操作を繰り返す。


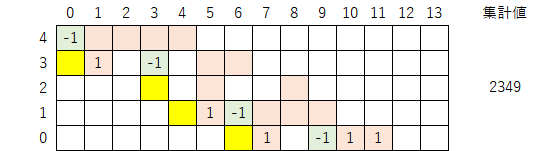
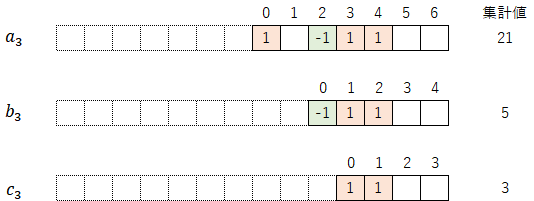
$${a_3=c_2\cdot3^1=21}$$
$${b_3=(a_3-1)\cdot\left(\frac{1}{2}\right)^2=5}$$
$${c_3=(b_3+1)\cdot\left(\frac{1}{2}\right)^1=3}$$

最終的に、以下のように$b_i$が「1」になるまで、この操作を繰り返す。


$${a_4=c_3\cdot3^1=9}$$
$${b_4=(a_4-1)\cdot\left(\frac{1}{2}\right)^4=1}$$

これらをまとめると以下のような関係式になる。

第10章 漸化式の一般化

ここで変数（$a_i$,$b_i$,$c_i$）を一般化する。そのために、以下のような関数を導入する。

$ν_p(n)$＝整数$n$を割り切れるような$p$-冪のうちの最大の冪指数
例：$ν_2(10)=1$ （$10=5\cdot2^1$なので）
　　$ν_2(48)=4$ （$48=3\cdot2^4$なので）

この関数$ν_p(n)$を用いることで、先ほどの漸化式は以下のように書き換えることができる。

添字$i=0$に対して（初期値設定）
$${b_0}=初期値$$
$${k_0=ν_2(b_0+1)}$$
$${c_0=(b_0+1)\cdot\left(\frac{1}{2}\right)^{k_0}}$$

任意の$i(i≥1)$に対して
$${a_i=c_{i-1}\cdot3^{k_{i-1}}}$$
$${h_i=ν_2 (a_i-1)}$$
$${b_i=(a_i-1)\cdot\left(\frac{1}{2}\right)^{h_i}}$$
$${k_i=ν_2 (b_i+1)}$$
$${c_i=(b_i+1)\cdot\left(\frac{1}{2}\right)^{k_i}}$$

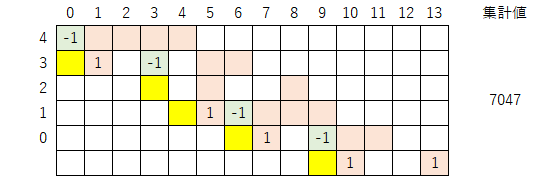
初期値29の場合、これらの変数($a_i$,$h_i$,$b_i$,$k_i$,$c_i$)は以下のような関係になる。

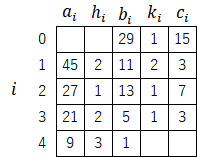
また、変数($h_i$,$k_i$)とマップとの関係は以下のようになる。

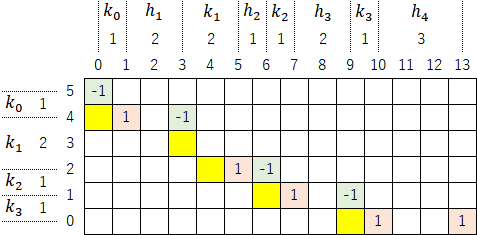
さらに、初期値29のコラッツ展開（29→88→11→34→17→52→13→40→5→16→1）のうち、奇数部分だけを取り出してみると、一つを除いて$b_i$と合致していることも分かる。

 
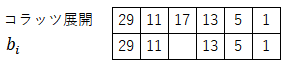
合致していない部分は、以下のように黄色マスが2段飛んでいる部分（太枠で囲まれている部分。本例では17）に該当する。この部分が含まれるように拡張することもできるが、本質的に重要ではないので、このまま進めることにする（※）。

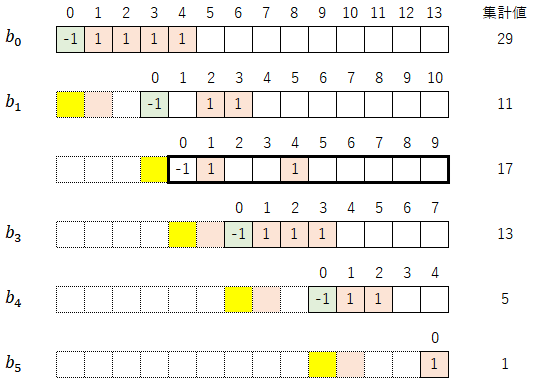
※）これは筆者の直感だが、コラッツ展開の数学的な本質はこの数列$b_i$であって、これまでのコラッツ予想（29→11→「17」→13→5→1 と「17」が入るパターン）は余分な要素が含まれ、かえって分かりにくくなっていると思う（きちんと数学的に説明できる話でもなく、あくまで直感だが）。

第11章 変数$b_i$の範囲（上限）

この変数$b_i$についてもう少し詳しく調べてみたい。そのために、他の変数($a_i$,$h_i$,$k_i$,$c_i$)を使って$b_i$を計算してみる。すると以下のようになる。

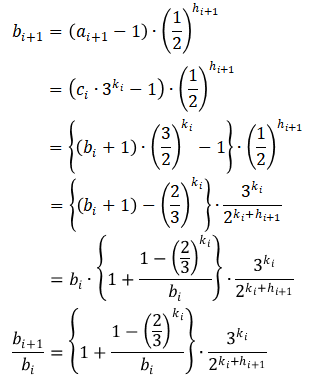
したがって、初期値$b_0$を使って変数$b_{i+1}$は以下のように表すことができる。

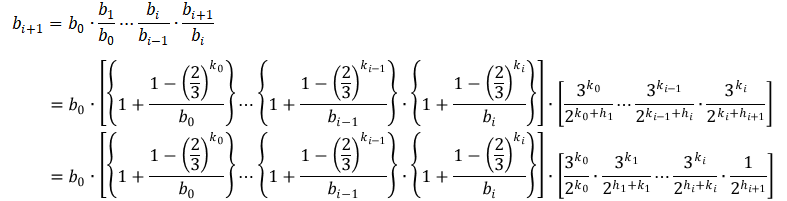
ここで、任意の$i(i≥1)$に対して、$0< k_i$かつ$3≤b_i$であるので、

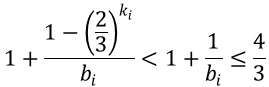
したがって、変数$b_i$に関して以下の関係式が成り立つことが分かる。これは変数($h_i$,$k_i$)の振る舞いを調べることで、変数$b_i$の範囲（上限）が分かることを意味する。

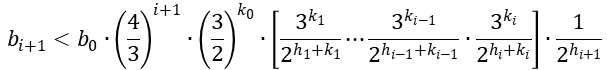
第12章 HK分布

さて、変数($h_i$,$k_i$)の振る舞いを調べてみよう。($h_i$,$k_i$)の定義は以下なので、どちらも変数$a_i$から計算することができる。
$${h_i=ν_2 (a_i-1)}$$
$${k_i=ν_2 (b_i+1)=ν_2\left((a_i-1)\cdot\left(\frac{1}{2}\right)^{h_i}+1\right)}$$

このことは、以下のように、マップ上での$a_i$と($h_i$,$k_i$)の関係を見ると分かりやすいかもしれない。

そこで、実際に各$a_i$から($h_i$,$k_i$)を計算して、その分布を調べてみた。すると、以下のような結果になった。
 

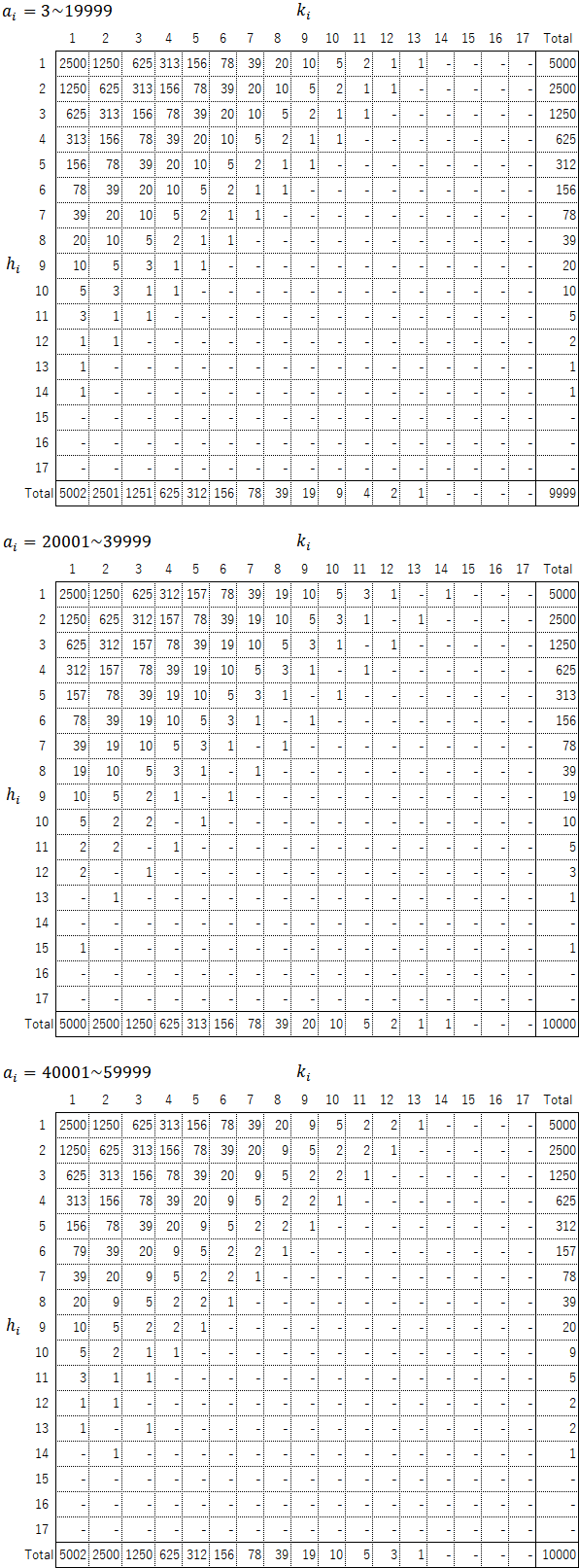
これらを見る限り、($h_i$,$k_i$) の組み合わせは常に以下の分布になりそうである。

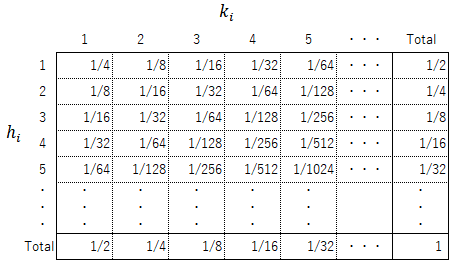
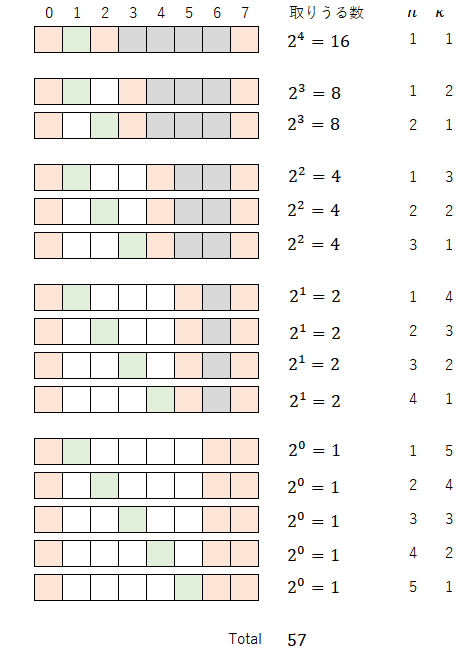
この分布を「HK分布」と名付けることにする。このHK分布は以下の説明からも理解できる話である。まず、次のようなパターンの数を全て列挙してみる（ここで、オレンジ色は「1」、緑色は「-1」、灰色は「0または1のいずれか」を表すものとする）。

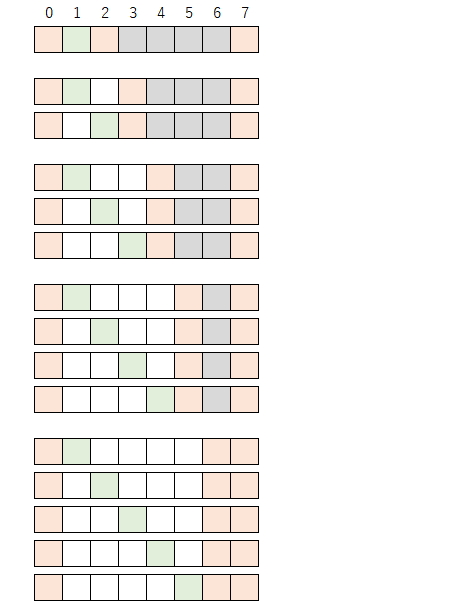
次にこれらのパターンが取りうる組み合わせを考える。オレンジ色と緑色は値が決まっており、灰色のみ値が変わるので、取りうる数は（灰色のマスの数を$n$として）$2^n$になる。その中で、変数($h$,$k$)の組み合わせを示してみると以下のようになり、HK分布はどの範囲の$a_i$でも成り立つと言えそうである。

第13章 コラッツ展開が収束することの確率的な検証

さて、この考察に基づいて、コラッツ展開したときの変数 ($h_i$,$k_i$) がHK分布に従うと仮定しよう。すると、($h_i+k_i$)の期待値$P(h_i+k_i )$と$k_i$の期待値$P(k_i)$はそれぞれ以下のように計算できる。
$${P(h_i+k_i)=\displaystyle\sum_{s,t}(s+t)\cdot\left(\frac{1}{2}\right)^{s+t}≅4}$$
$${P(k_i)=\displaystyle\sum_{s}s\cdot\left(\frac{1}{2}\right)^s≅2}$$

したがって、十分に大きな$i$に対しては、確率的に以下の式が成り立つことになる。
$${P\left(\displaystyle\sum_{q=1}^{i}(h_q+k_q)\right)=\displaystyle\sum_{q=1}^{i}P(h_q+k_q) ≅4i}$$
$${P\left(\displaystyle\sum_{q=1}^{i}k_q\right)=\displaystyle\sum_{q=1}^{i}P(k_q ) ≅2i}$$

なお、このことから、十分に大きなコラッツ・マップでは、縦横の比が1:2に限りなく近づくことも分かる。この性質も後ほど必要となるので、覚えておいてほしい。

さて、上記の性質を使うと、十分に大きな$i$に対しては、$b_{i+1}$は確率的に以下のように計算することができる。

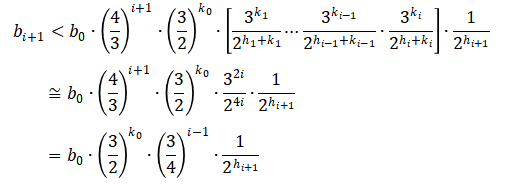
これは、「$i$を十分に大きくした場合」すなわち「コラッツ操作を繰り返して、マップを十分に大きくした場合」には、$b_{i+1}$は発散せずに一定の値以下に落ち着くことが、確率的に強く期待できることを意味している。

第14章 コラッツ展開がループしないことの確率的な検証

コラッツ予想が成り立つためには、以下の条件が必要十分となる。
　　①コラッツ展開が発散しない
　　②コラッツ展開の途中で同じ値を取らない（ループしない）
このうち条件①に関しては前章で確率的に強く期待できることを示した。本章では条件②に関して考えてみたい。

そのために以下の条件③を検討する。
　　③ある初期値Xのコラッツ展開では途中で同じ値が現れる（ループする）
言うまでもなく、この条件は②と背反している。本章では条件③が成り立つとき、どのような状況になるかを見ることにする。

まず、条件③を満たす初期値$X$があるとして、それを以下のように表す（ここで、オレンジ色は「1」、緑色は「-1」、灰色は「0または1のいずれか」を表す）。なお、本例では最左端の緑「-1」とオレンジ「1」が隣接しているが、これは一つの例である。実際には常に隣接しているとは限らないが、そこは本筋には関係ないので、特に気にせず進んでいただきたい。
初期値$X$のマップ

さて、この初期値$X$から始まるコラッツ・マップを考えてみる。ここでは、マップが以下のようになったと仮定しよう（このマップを「$M_X$」と名付けることにする）。
マップ$M_X$

条件③より、マップ$M_X$の右下には以下のように初期値$X$が現れることになる（太枠で囲まれた部分）。なお、見やすさのため、以後は特に必要のないマークはマップから消しておく。
マップ$M_X$

次に、以下のようなマップ「$M_X’$」を考える。これはマップ$M_X$から右下の$X$を除いたものである。
マップ$M_X’$

さらに、この後の議論で使いやすいように、マップ$M_X’$を以下のように変形させておく（黄色マークに数字を移動させる）。このような変形を加えても集計値は変わらないことは、これまでの議論からお分かりいただけると思う。
マップ$M_X’$

さて、マップ$M_X$は初期値$X$から始めたものであるので、条件③が成り立つためには、以下の二つのマップの集計値が同じになることが必要となる。
初期値$X$のマップとマップ$M_X$

そのため、マップ$M_X’$の集計値を「$S$」とすると、条件③が成り立つためには、初期値$X$と$M_X’$の集計値$S$との間には以下の関係が成り立つことが必要となる。
$${3^m \cdot X=S+2^n \cdot X}$$
$${X=\frac{S}{\left(3^m-2^n\right)}}$$

そこで、$S$と$(3^m-2^n)$の関係について調べてみたい。まず、$(3^m-2^n)$は以下のようなマップとして表すことができる。
$(3^m-2^n)$のマップ

ここで少し話が飛ぶが、HK分布を思い出してほしい。HK分布がここで取り上げているマップでも成り立つと仮定すると、十分に大きなマップに対しては、以下の近似が成り立つことが期待できる。
$${n≈2m}$$

そこで、ここでは $n=2m$ が成り立つものと仮定する。その場合、$(3^m-2^n)$のマップは以下のようになる。
$(3^m-2^n)$のマップ

さて、ここでマップ$M_X’$をもう一度見てみよう。すると、若干の違いはあるが、$(3^m-2^n)$のマップとかなり似ていることが分かる。
マップ$M_X’$

もちろん、完全に一致しているわけではないが、この類似性から、$S$と$(3^m-2^n)$ は非常に近い値を取ることが予想され、初期値$X=S⁄(3^m-2^n)$も相対的に小さな数になることが推察される。

では、この推察が実際に妥当かどうかを考えてみたい。そのために、HK分布を使って仮想マップをいくつも生成し、モンテカルロ・シミュレーションで$S$と$(3^m-2^n)$の関係を調べてみた。すると、以下のような結果が得られた（見やすいように両変数とも正に変換し、両軸も対数にしている）。これを見る限り、$S$と$(3^m-2^n)$はほぼ近い値を取っていると言えそうである。

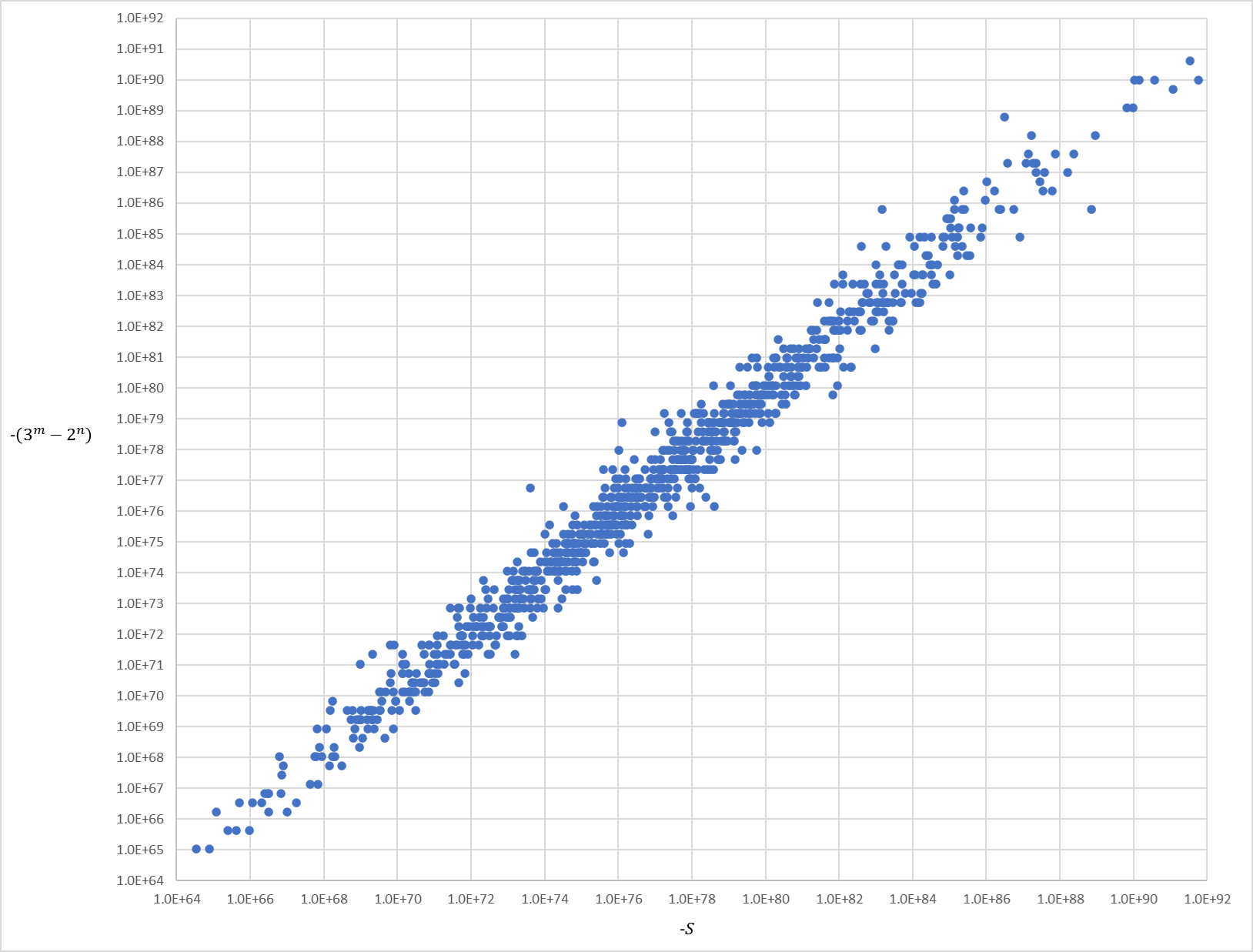
さらに、これらのデータを元に$S⁄(3^m-2^n)$の分布（正確には$\log_{10}⁡[S⁄(3^m-2^n)]$ の分布）を計算したところ、以下のようになった。対数の分布なので$10^3$ までデータの範囲が広がっていることになるが、元データ（$S$と$(3^m-2^n)$）の範囲が$10^{64}\sim10^{92}$なので、その値は相対的にかなり小さいと言えるだろう。

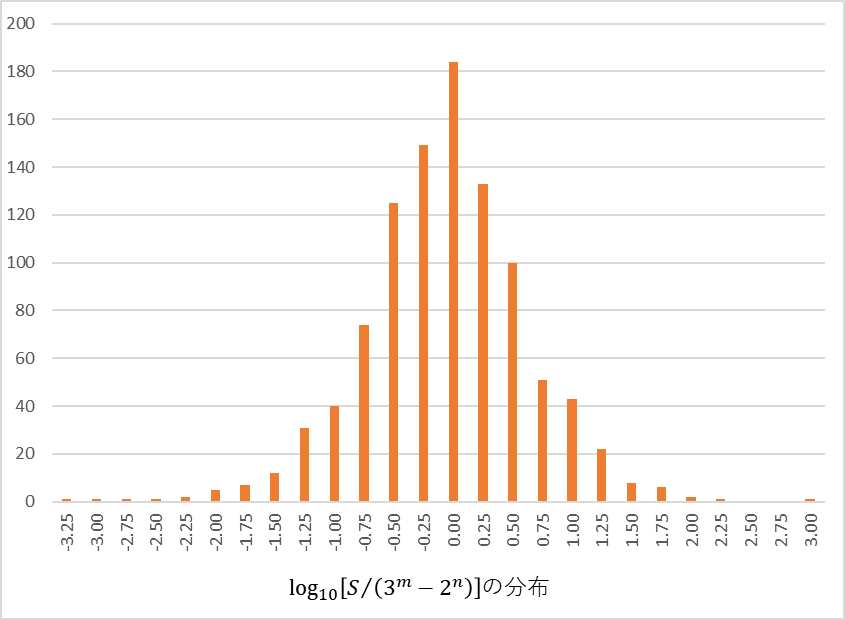
ということで、ここまでの話を整理したい。条件③（コラッツ展開がループする）が成り立つためには、初期値$X$と$M_X’$の集計値$S$との間に以下の関係が成り立つ必要があると述べた。
$${X=\frac{S}{\left(3^m-2^n\right)}}$$

しかし、HK分布を前提に考えると、$S⁄(3^m-2^n)$の値はマップの大きさに比べてかなり小さくなる。すなわち、条件③が成り立つのは確率的に極めて小さいと言えそうである。

第15章 初期値「27」や「31」のコラッツ展開が大きくなる理由

コラッツ展開には一つの大きな特徴がある。隣接した初期値から始まったとしても展開される数列が似たものになるとは限らず、時には（「常に」ではないが）大きく異なる様相を見せる場合があることだ。また、ごく小さな初期値から始まっているにも関わらず、展開した数列が奇妙なほど長く続くものも時々見られる。つまり、コラッツ展開には「初期値がわずかでも異なれば、そのわずかなズレが最終的に大きな違いにつながる」という一種のカオス的な性質が内包されているようだ。

本章では、そうしたカオス的な側面について、少し詳しく見ていきたいと思う。

コラッツ展開を順番に調べていくと、下記の初期値「27」や「31」のように、前後の初期値と大きく異なる振る舞いを見せるものがある。

この理由を紐解くために、各初期値（27と31は除く）のコラッツ・マップを表示してみよう。当然だが初期値ごとに描かれるマップは異なっている。しかし、どれも最終段階では似た形になっていることが分かるだろう。

筆者は様々なコラッツ・マップを調べてみたが、ほとんどの場合は上記と同様のパターンで収束していた。全ての初期値で同じようなパターンで終わるかはさらなる検討が必要だが、少なくともこのパターンで終わる場合が多いことは言えそうである。

そこで、この点についてもう少し詳しく調べてみたい。まずは次の3つのパターンから始まるコラッツ・マップを考えてみる。

これらのパターンから始まるコラッツ・マップを描いてみると以下のようになり、それぞれ数段階を経て収束することが分かる。つまり、上記の3パターンのいずれかがマップの中に見つかれば、そこから収束までは「あともう一息」ということになる。

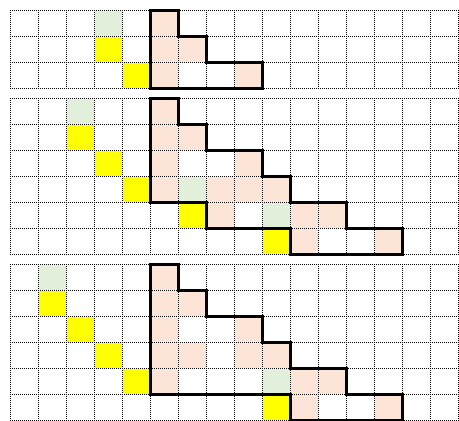
ただ、このようなパターンで始まるマップが直ぐに収束に向かうとは限らない。試しに、上記3パターンよりも、もう一マス間隔が広がった以下のマップを考えてみよう。

このパターンから始まるマップの場合、途中までは収束するパターンと同様だが、そこで終わらず、以下のように先々まで広がっていくことになる。

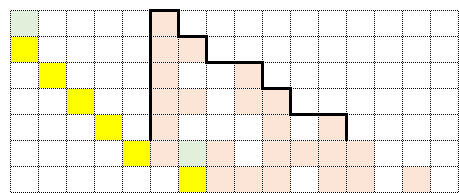
実は初期値が27や31がこの広がっていくパターンに該当する。そのため、この両者では、マップがすぐに収束せず、下に大きく伸びていくことになるのだ。

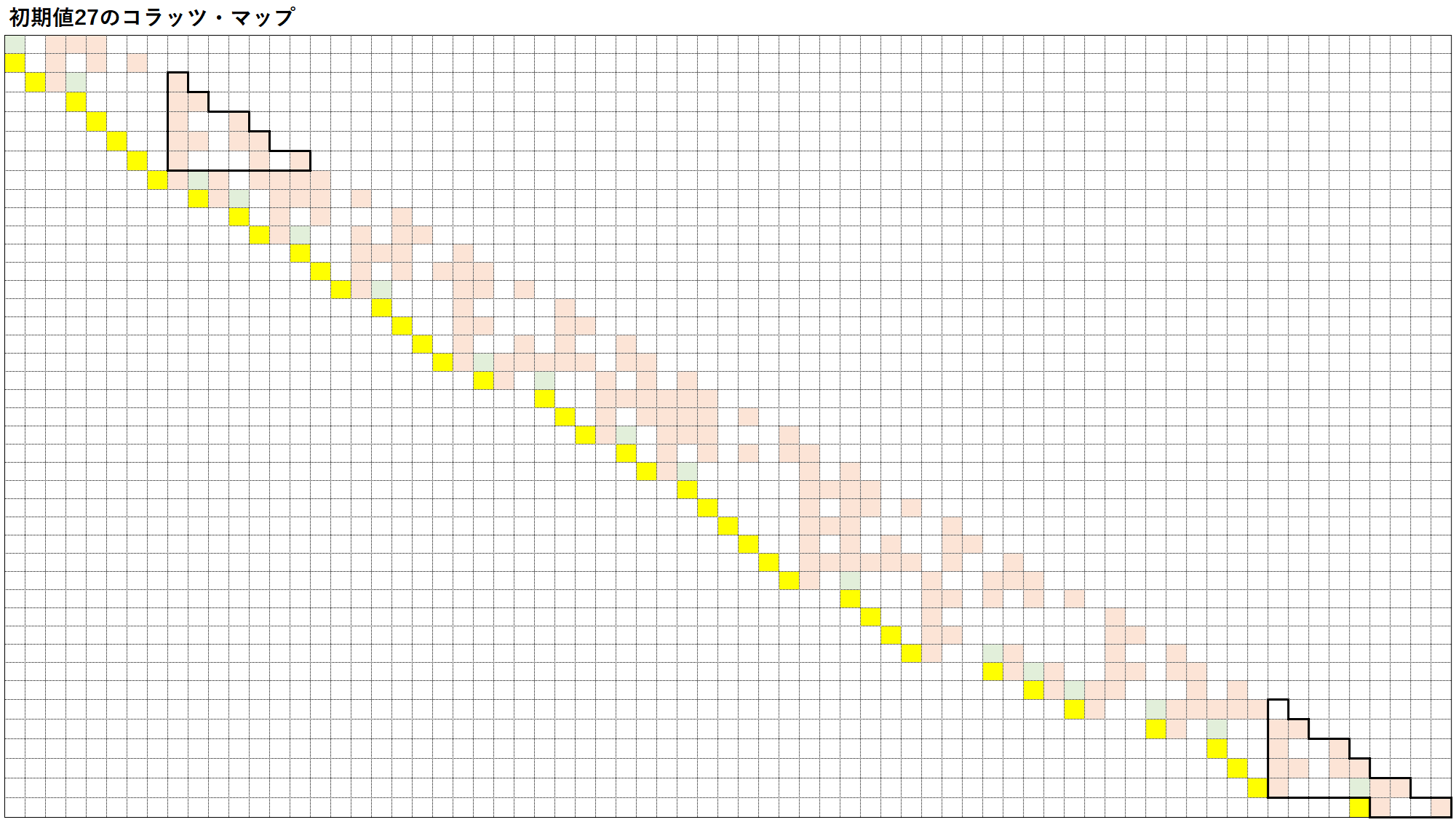
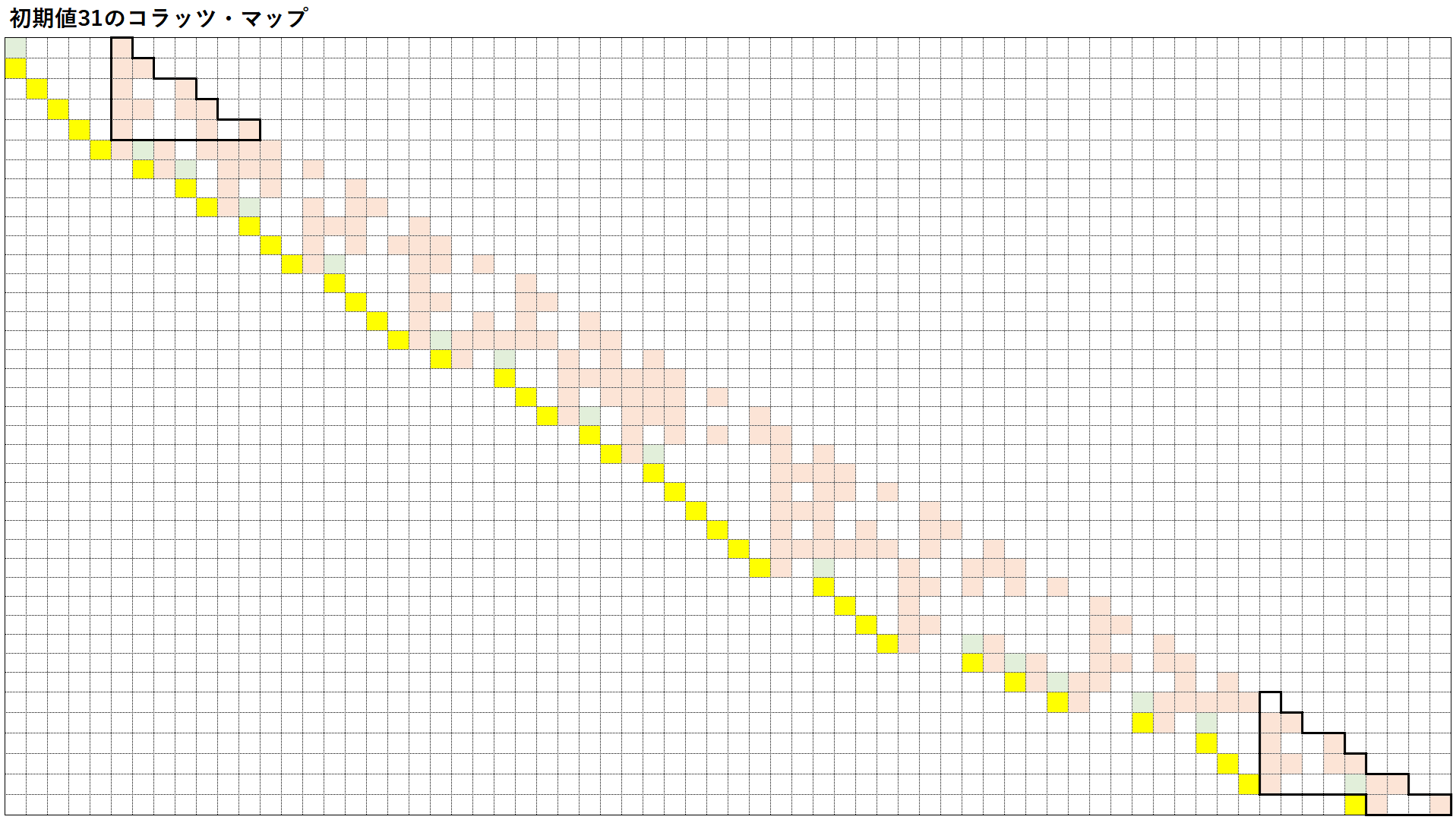
参考までに、初期値が27や31のコラッツ・マップを以下に表す。両マップとも最終的には収束するが、いったんは下に大きく伸びていることが分かるだろう。似たような初期値と思えても、数字が置いてある位置が一つ違うとその後の展開が大きく異なることを如実に示している好例と言えるかもしれない。

第16章 終わりに

本稿はこれで終わりとする。筆者は元々物理出身であるので、本稿での議論でコラッツ予想の成立を強く確信できたが、数学の専門家から見れば物足りない点もあるかと思う。 一方で、本稿で用いたアイデアは、手前味噌ながらシンプルかつ網羅的にコラッツ予想の特徴を説明できており、我ながら中々面白い着眼点かなと考えている。本論考に興味を持たれた方は、是非とも論を先に進めていただきたい。