滑らかな斜面上での物体の運動

記号一覧

　$g\ \cdots$重力加速度$\ \ [ms^{-2}]$
　$x$軸$\ \cdots$斜面に沿って上から下に引いた軸
　$x_0\ \cdots$物体の最下点の座標$\ \ [m]$
　$m\ \cdots$物体の質量$\ \ [kg]$
　$x\ \cdots$物体のx軸方向位置$\ \ [m]$
　$v\ \cdots$物体のx軸方向速度$\ \ [ms^{-1}]$
　$a\ \cdots$物体のx軸方向加速度$\ \ [ms^{-2}]$
　$k\ \cdots$バネ定数$\ \ [kgs^{-2}]$
　$t\ \cdots$初期時刻からの経過時間$\ \ [s]$
　$\theta\ \cdots$斜面の角度$\ \ [rad]$
　$const\ \cdots$「時間によらず一定の数」の意味で用いられる。この記事では力学的エネルギーを表す。

状況設定

角度$\theta$の滑らかな斜面上に質量$m$の物体がバネに繋がれている。この時の物体の運動について考える。

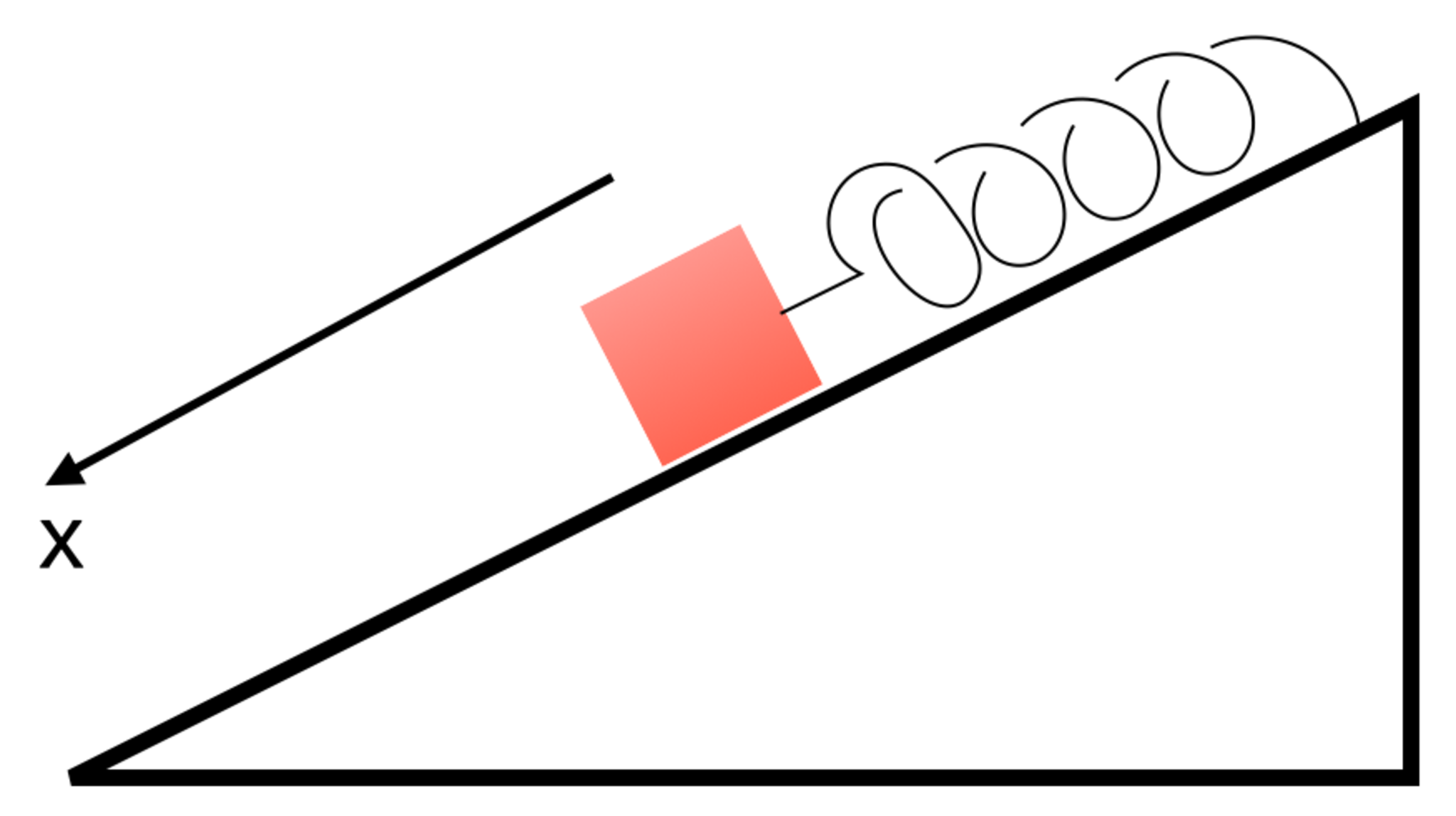
座標系の定義

斜面に沿って、高い方から低い方に$x$軸を取る。また、バネの自然長における地点を$x$軸の原点とする。

運動方程式とエネルギー保存

この時、$x$軸方向の運動方程式は
$$ma = mgsin\theta - kx$$
　この運動方程式より導かれるエネルギー保存は
$$\frac{mv^2}{2}-mg(x-x_0)sin\theta+\frac{kx^2}{2}=const\ \ \cdots (1)$$
※重力の位置エネルギーの基準は最下点$x_0$で取る。

初期条件を具体的に設定した時

一つの具体例としてバネの自然長の位置で静かに物体を離した時を考えると、初期条件は$x(0)=0,v(0)=0$となる。

最下点を力学的エネルギー($const$)保存則から求める

エネルギー保存の式(1)を用いると

(i)初期時刻にて：$x(0)=0,v(0)=0$が満たされるので、
$$\ \ \ \ \ \ \frac{m\cdot 0^2}{2}-mg(0-x_0)sin\theta+\frac{k\cdot 0^2}{2}=const$$
$$\Leftrightarrow mgx_0sin\theta=const\ \ \cdots(2)$$

(ii)最下点$x=x_0$にて：$v=0$が満たされるので、
$$\ \ \ \ \ \ \frac{m\cdot 0^2}{2}-mg(x_0-x_0)sin\theta+\frac{k x_0^2}{2}=const$$
$$\Leftrightarrow \frac{k x_0^2}{2}=const\ \ \cdots (3)$$

よって、(2)(3)より$\displaystyle mgx_0sin\theta = \frac{kx_{0}^2}{2} \Leftrightarrow x_{0}=\frac{2mgsin\theta}{k}\ \ \cdots (4)$

$x_0$が求まったので力学的エネルギー$const$を求める

(3)の$x_0$に(4)を代入して$\displaystyle const=\frac {2m^2g^2sin^2\theta}{k}\ \ \cdots (5)$となる。(※(3),(4)ではなく (2),(4)を用いてもよい)

力学的エネルギー$const$が求まったので改めてエネルギー保存則を書き直す

エネルギー保存則(1)を改めて書き直す。(4),(5)より$x_0, const$を(1)に代入する事で以下を得る。
$$\ \ \ \ \ \frac{mv^2}{2}-mg(x-\frac{2mgsin\theta}{k}) sin\theta+\frac{kx^2}{2}=\frac {2m^2g^2sin^2\theta}{k}$$
$$\Leftrightarrow \frac{mv^2}{2}-mgx sin\theta+\frac{kx^2}{2}=0\ \ \cdots (6)$$

振幅を求める

振幅は最も物体が大きく振れている座標を2つ求めてそれを2で割れば良い。

振幅が最も振れている時は速度について$v=0$が成立するが、それは今の場合$x=0,x_0=\displaystyle \frac{2mgsin\theta}{k}$で満たされる。
　よって振幅はこれの半分で$\displaystyle \frac{2mgsin\theta}{k} \div 2 =\frac{mgsin\theta}{k}$

中心における速度を求める

振動中心の座標は、初期地点$x=0$と$x_0=\displaystyle \frac{2mgsin\theta}{k}$の中間地点$\displaystyle x=\frac{mgsin\theta}{k}$である。この地点での速度はエネルギー保存則(6)に$\displaystyle x=\frac{mgsin\theta}{k}$を代入して
$$\ \ \ \ \ \frac{mv^2}{2}-\frac{m^2g^2 sin^2\theta}{k}+\frac{m^2g^2sin^2\theta}{2k}=0$$
$$\Leftrightarrow \frac{mv^2}{2}=\frac{m^2g^2sin^2\theta}{2k}$$
$$\Leftrightarrow v^2=\frac{mg^2sin^2\theta}{k}$$
$$\Leftrightarrow v=\pm \sqrt{\frac{m}{k}}gsin\theta$$
速さは$\displaystyle |v|=\sqrt{\frac{m}{k}}gsin\theta$