【正単体】n次元にn+1個の点を互いに距離を等しく非負座標に置く公式

133

$n$次元に“非負座標”だけで組み上げる正単体

公式の前に

正単体ってなに？

正単体(regular simplex)
-$n$次元上の互いの距離がすべて等しい$n+1$点
$n$次元上には、等距離の点が最大$n+1$個置けることが知られています。
$2$次元平面上に、互いの距離が等しい$3$点は正三角形をつくる要領で置けるね。

再帰的に求め、一般化します

本来は「Gram行列」やら、いろんな方法で求めるようですが、僕は何も知りません。
互いの距離を1と決め、原点からスタートし、一本ずつ次元を増やし、非負座標で定めていくと、一意に定まります。
その座標の公式を求めれました。既によく知られたものでしたらごめんなさい。

座標公式

$n$次元内に$n+1$個の点$p_1$～$p_{n+1}$を互いの距離を等しく置いたときの座標（距離=1、原点スタート、次元を一つずつ追加しながら、非負座標）

$p_1 = (0, 0, … , 0)$
$p_2 = (b_1, 0, … , 0)$
$p_3 = (a_1, b_2, 0, … , 0)$
$p_4 = (a_1, a_2, b_3, 0, … , 0)$
$p_5 = (a_1, a_2, a_3, b_4, 0, … , 0)$
$…$
$p_{n+1} = (a_1, a_2, … , a_{n-1}, b_n)$

$a_k= \frac{1}{\sqrt{2k(k+1)}} , b_k=\sqrt{\frac{1}{2}(1+\frac{1}{k})}$
$(k=1,2,3,...,n)$

※距離$=r$にしたいときは、全体を$r$倍すればよい。

求める過程（アルゴリズム）

例えば$xyz$空間の時、
最初に$p_1=(0,0,0)$を定め、
$p_1$からの距離が1となる点の条件は$x^2+y^2+z^2=1$...①
①から$y,z$を$0$のまま条件を満たす$x$のうち非負の実数$1$を用いて
$p_2=(1,0,0)$とする
$p_2$からの距離が$1$となる点の条件は$(x-1)^2+y^2+z^2=1$...②
①,②から、$z=0$$(z軸は用いない)$で$x=\frac12$と非負の$y=\frac{\sqrt3}{2}$が得られ
$p_3=(\frac12,\frac{\sqrt3}{2},0)$
...とこのように続く。
解く過程から、$a_k,b_k$は定まる。

例

$3$次元に$4$点$(n=3)$点と点との距離は1

公式により、
$p_1 = (0,0,0)$
$p_2 = (1,0,0)$
$p_3 = (\frac{1}{2},\frac{\sqrt3}{2},0)$
$p_4 = (\frac{1}{2},\frac{1}{2\sqrt3},\frac{\sqrt2}{\sqrt3})$
$p_1,p_2,p_3,p_4$間はそれぞれすべて距離が1です。
一辺の長さが$1$の正四面体の頂点を三次元空間においた感じです。
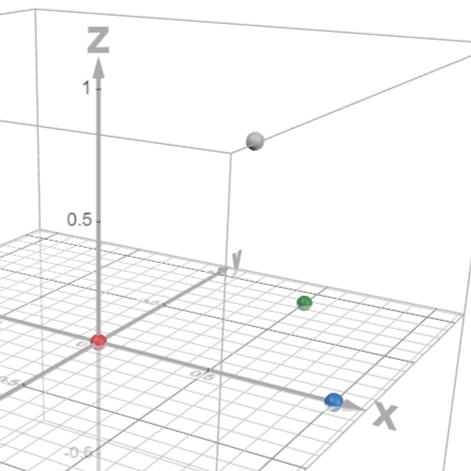3dimentional/Desmos