sin cos tan ←なんでそんなにチヤホヤされてんの？！？！

　こんにちは、普段は数学部の活動の一環として数オリ対策問題集を投稿しているみねみねです。

　ところでみなさん、「三角関数」及び「サイン・コサイン・タンジェント」という言葉に聞き馴染みはあるでしょうか？　人間、生きていれば一回は聞いたことがあるかも知れません。また、「高校数学でつまづくところ」という矢鱈と弱気な解釈をしている人もそう少なくないかと思います。

　もしくは、「三角関数って習う必要ないだろ！！！！！！！」と豪語する三角関数アンチもいるかもしれません()

　いいえ、三角関数は、数学の根幹を支える超重要な概念なのです！

　どこで役に立つかは多岐にわたり、

・習いたてのときは "幾何学(図形を研究する学問)" で、
・さらに進むと "代数学(計算法則を研究して数学の共通言語を作る学問)" で、
・さらには "解析学(関数の性質について研究する学問)" で

　その強力さを発揮します。いわゆる「神ツール」です。

　ってなわけで、そんなみなさんに三角関数の偉大さをわからせてあげましょう！！！(筆者は最近そういうものにハマっている)

やること

(0.ラジアンと三角関数の定義)
1.三角形の面積と余弦定理
2.三角関数の具体的な値を求める(加法定理/倍角・半角公式)
3.三角関数の微分とマクローリン展開
4.三角関数を用いる置換積分
5.複素平面と三角関数とオイラーの公式

ではいく〜！

0. ラジアンと三角関数の定義

角度の新たな定義

　$1 \degree,2 \degree,3 \degree,\cdots$と続く度数法. その定義をみなさんはパッと言えるでしょうか？　なんだか当たり前すぎて定義に帰ることってないですよね. まあ、次のように定義すればいいんじゃないでしょうか.

　そういえば小学校でこんな習い方をしたような気もしますね(ずいぶんと昔の話でよく覚えていませんが).
　しかし, この角度の表し方ってなんだか不思議じゃありませんか? わざわざ円周を "360" という数字で分割しているところとか, そもそもなんで "360" なんだろうって話です. 1周を「1」とするのでなく「360」とするのはだいぶキモいことに思えます.

　だったら, 最初から等分なんてしないで「弧の長さ」とかで角度を定義してあげたらいいんじゃないでしょうか? そうして定義できるのが「弧度法」ってヤツです.

　はじめはこの定義にキレそうになるかもしれませんが、のちのちこれが効いてきます(とくに微分あたり).

　ってなわけで、急に問題を出しましょう. 先にヒントを与えると, 中学1年生の定期テスト小問集合の最後の方らへんにある問題です.

　ってことで度数法に慣れ親しんだ今までの私たちとはおさらばです！！これからはこの弧度法を死ぬほど使っていくので頑張ってついてきてください.

三角関数とはなにか

　いよいよ三角関数の定義をしていきます. 定義を聞いてキレないでください(言いましたからね?).

(つまり$\tan \theta$は "直線$AO$" と "直線$x=1$" の交点の$y$座標とも捉えられる.)
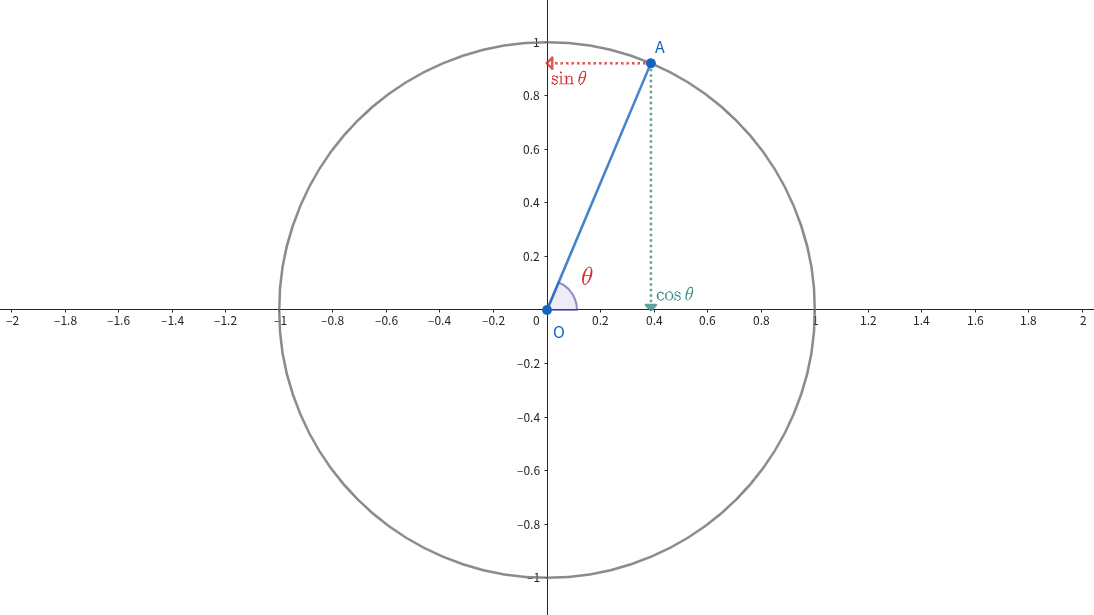sinとcosのイメージ

　はい, これが三角関数-すなわち"sin,cos,tan"の定義です!

　(...)

　(...よし, キレてないな...?)

　(...よかった, よかった...)

　(...いや, 気づかれたか...?!)

　(...まずい, 完全に気づかれた!!!!)

　ぎゃぁ〜〜!!!! 許してください!!! 確かにみなさんの「どこにも "三角" が出てこないじゃないか！」っていう気持ちもわかります!!! これは私がひとステップ飛び級して定義したせいなんです!!! でも, 次の公式を見たらちょっとは納得がいくのではないでしょうか?!?!?!

　はい. 確かに三角形が出てきましたね(冷や汗).

　...って, 流石にこれだけで受け入れてくれる人はそう多くないと思うのでもうちょっと「三角」要素について考えていきます.

　証明に出てきた$\triangle AOH$ですが, これは

• 斜辺が$1$
• $\theta$の対辺が$\sin \theta$
• 上の２つで取り上げなかった辺が$\cos \theta$

　という直角三角形です. 実は, 三角関数が産声を上げたとき, その定義は上の$\triangle AOH$そのものでした. つまり, 斜辺が$1$の直角三角形において$\theta$の対辺を$\sin \theta$と定義したのです. この定義だと「三角関数」という名前にも納得がいきます.

　しかし, 数学者たちは三角形を考えるだけでは物足りませんでした. なぜなら, 三角形で定義した三角関数は定義域が$0 \lt \theta \lt \frac{\pi}{2}$に限定されていたからです!!!

　$\sin 120\degree$や$\tan (-720\degree)$のようなものも考えたい...

　そうした欲求から, 三角関数を, より拡張した「円での定義」で考えるようになったのです!

　ってなわけで, 三角関数の値を求める簡単な問題を解いてみましょう.

　こんな感じで,有名角は求めることができます.
　また, 4つの問題では扱いませんでしたが, $\sin 120\degree=\frac{\sqrt{3}}{2}$のように円を考えることで様々な角度が求められます(「$120\degree$のときって, つまり第2象限に$1:2:\sqrt{3}$の直角三角形ができるときだなぁ」という発想).

　$\theta=135\degree(=\frac{3}{4}\pi)$のときの$\sin,\cos,\tan$なんかも暇つぶしに求めてみてください.

1. 三角形の面積と余弦定理

　ここから, 一気に応用編です. まさか, 定義だけで三角関数のありがたみを感じられる人なんていないでしょう. これから私達は中学数学(図形分野)での「点と点とがつながっていく感覚」を味わいます. ここからがお楽しみポイントですので, 楽しんでください!

三角形の合同条件

　三角形の合同条件って, いくつかありましたよね.
　私は「3+2個」って意識で覚えているんですけど, 同じ人いるんですかね...

　ってな訳で, 合同条件を5個書いていきます.

　定理1〜3の証明は本題から逸れるのでしません.

　では, 定理4の証明をします.

　よくよく考えたら当たり前でしたね(なお, 合同条件は中二で, 三平方は中三の最後で習うらしいですが...).

　このままの勢いで定理5も証明します.

　この証明に出てきた「相似」が, 三角関数ではとても大事です.

　斜辺が$r$のとき, $\theta$の対辺は$r\sin \theta$になりますし, もう一つの辺は$r\cos \theta$になります.
　この考え方は三角関数を使う上で必ず使うのでちゃんと理解して使えるようになりましょう!

三角形の面積を合同条件②から求める

　いきなりですが, 三角形の面積公式というのはたくさんあります.

　たとえば「ヘロンの公式」なんてものがありますね? あれは三辺の長さが分かれば一瞬でその三角形の面積が求められるってやつです.

　これって, 三角形の合同条件①の考え方にとっても準拠していませんか?
　三辺が決まれば三角形が決まるので, その面積は3つの辺の長さの情報のみに依存するはずです. つまり, 辺の情報だけで面積が書けるはずです!
　それが, ヘロンの公式の気持ちです.

　では, 合同条件②の考え方に準拠した面積の公式はあるのでしょうか?

　二辺とその間の角が決まるらしいので,その２つの辺の長さをそれぞれ$a,b$として, 間の角を$\theta$とでもしましょう.
　このとき, 下のような図を考えると, もう今のあなたなら面積を求めることができそうです...!
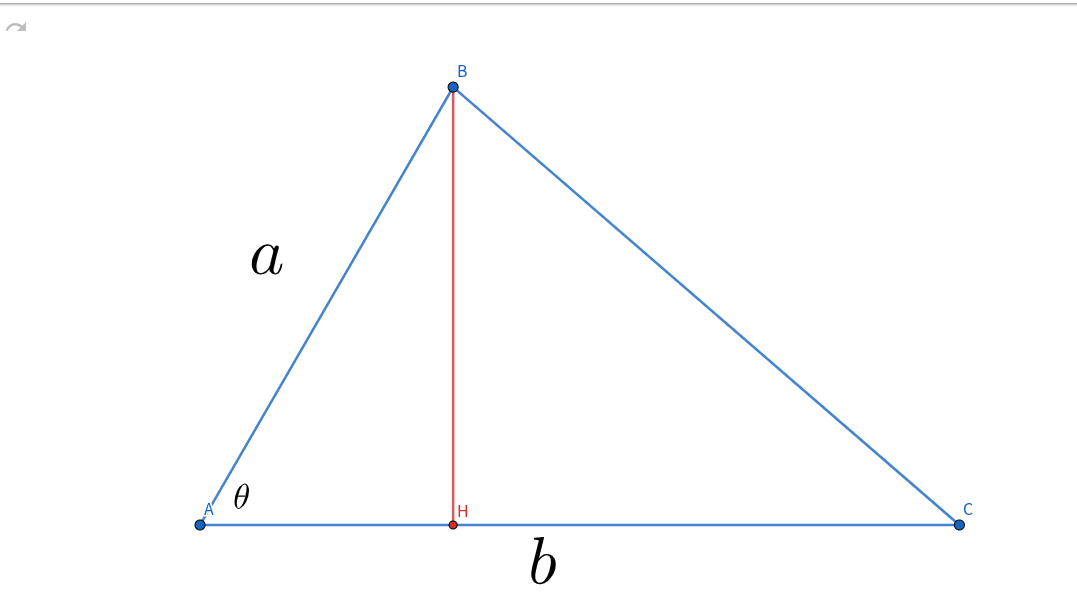二辺とその間の角から面積を求めよう

$AH$を用いて面積を記述する

　$\triangle ABC=S$とするとき, $S=b\cdot AH\cdot \frac{1}{2}$である.(底辺$\times$高さ$\times \frac{1}{2}$)
　計算し, 次式を得る.

$${S=\frac{1}{2}AH\cdot b}$$

$AH$を$a$や$\theta$で表現する

　さきほどの「証明：三角関数→定理4へ」と同じように考え, $AH=a\sin \theta$
　これを代入し, 次式を得る.
$${S=\frac{1}{2}ab\sin \theta}$$

　これで合同条件②に準拠した面積公式が得られました!
　当然な話ではあるのですが, 角度が与えられたらだいたいは三角関数を使えば求めたいものが求まります. 三角関数に慣れてきた方々は合同条件③に準拠した面積公式も導いてみてはいかがでしょうか.

三平方の定理を合同条件②で拡張する

　先ほどと同じように, 三平方の定理を合同条件で解釈してみましょう.

斜辺がわからないとき　→合同条件②

　二辺とその間の角(これは直角)が決まるため, 三角形が決定し, 斜辺の長さも決定される.

斜辺以外がわからないとき　→合同条件④

　直角三角形で斜辺と他の一辺が決まるため, 三角形が決定し, 分からない辺も決定される.

　合同条件に着目すると, 三平方の定理は2通りの気持ちがあるのですね(わざわざこの違いを意識する必要はないのですが).
　では, この「合同条件②の三平方の定理」について, 拡張した定理を考えてみましょう.

拡張のしかたとして考えられるもの

　与えられているものは二辺$a,b$とその間の角$\frac{\pi}{2}$.
　分からないものは$\frac{\pi}{2}$の反対側の辺であり, これを$c$とする.

　→拡張・一般化とは, 具体的な数値を文字で表すことなので, $\frac{\pi}{2}$を文字に置き換えるしかない.

　先に定理の形として書いてしまいます.

　三平方の定理$a^2+b^2=c^2$にちょっとだけ項が増えただけですね.
　ちょっと証明してみましょう.

　やぁぁぁったぁぁぁ！！！！　もう, なんとなく三角関数の強力さに気づいてきているのではないでしょうか! 上で示した公式や定理を使って新しい様々な定理を示すことができます.
　面積公式や余弦定理の練習問題はここでは出しませんが, ネットや参考書なんかに転がっているので然るべきときにやりましょう.

2. 三角関数の具体的な値を求める

sin75°はどんな値?

　いままで, $\sin \frac{\pi}{4}$や$\tan \frac{\pi}{3}$などを求めてきました. しかし, これらは有名な角度での値に過ぎません. 三角比を知っていたから脳死で解けただけです.
　では, $\sin \frac{5}{12}\pi(=75\degree)$などを求めることはできないのでしょうか?
　実は, 以下の公式を使って求めることができます.

また、$\tan(\alpha+\beta)=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)},\tan(\alpha-\beta)=\frac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)}$より,次式を得る.

　ここではtanのみを証明する. ちなみに, sin,cosの証明は実は余弦定理を用いてすることができるが, ここではしないことにする.

加法定理において, $\alpha=\beta=\theta$とすることで倍角公式を得る.

cosの倍角公式から半角公式を得る(下に証明あり).

　これらの覚え方についてのアドバイスです.
　まず、sinとcosの加法定理を覚えましょう！ これらは使っているうちに覚えられますが, 実際に加法定理を使う問題に出会う前は語呂合わせで覚えましょう(いわゆる「咲いたコスモスコスモス咲いた」「幸子小林小林幸子」のこと).
　これらを覚えたら, tanの加法定理は上の証明のとおりにすれば導けます.
　また, 倍角公式も$\alpha=\beta=\theta$を代入するだけなので導けます.
　さらに, 倍角公式を導いたらそこから半角公式を導けます.

　これは数学あるあるなのですが, 「公式を覚える」ではなく, 「導出を覚える」ほうが圧倒的にラクです. 数学者は, 四次方程式の解の公式(フェラーリの公式)を覚えていないものの, その導出は完全に覚えているので, その場で公式を作ることができます.

　分かりましたか？ 勉強するときは「導出を覚える」!
　これはとても大切なことなので本題からは逸れますが強調して書きました.

　じゃあ, 今手に入れた道具を使ってsin15°を求めましょう.

　はい. こんな感じで求めることができます.

　また, 今の知識であの超有名問題が解けるので, 解いてみましょう!

　(こんなにも短い最終問題があっていいのか!!!!!!)

　一度, 自力で解いてみてください!!!

　この問題の回答はあえてこの記事には残しません. 解説はネット上に死ぬほど転がっているので解けたら探してみてください.

3-1. 三角関数の微分

　ところで, いままで三角関数を「幾何的な概念」として扱ってきました.
　しかしながら, 「関数」という名を預かっている以上, 解析的な研究もしてみたいわけです.
　というわけで, 今からは考える世界を解析の世界に変えて, 三角関数を「関数」として扱っていきましょう!

サインカーブ

　今まで$\sin\theta$のように表現してきた三角関数で,$y=\sin x$のグラフを考えてみます. 第0章で考えたように, ここで$x$は任意の実数をとることができます.
　まあ, 百聞は一見に如かずってわけで早速グラフを見てみましょう.
$y=\sin x$のグラフ

気づくこと

• $y=0$は,$x=n\pi$$(n=0,1,-1,2,-2,\cdots)$のとき
• 常に$-1 \leq y \leq 1$が成り立つ
• $x$が$2\pi$動くごとに同じ形が繰り返される

　こんな感じですかね. 第0章での定義を考えればどれも当たり前の性質ですね.
　ちなみに, これは現段階で理解しなくていいんですけど, このグラフの1つの山の面積はちょうど2です(!!!!) なんかえもいえない感動があります!

微分がしたい

　微分を習っていない人向けに「微分とはなにか」を軽く触れておくと, 微分とは「関数を別の関数にする手法の一つ」です. もうちょっと具体的にすると, 「関数のある地点$x$における傾きを値にもつ新たな関数をつくること」が微分です.
　たとえば,「$y=ax+b$(一次関数)」を微分することを考えてみましょう.

• $x=1$のとき, グラフの傾きは$a$です.
• $x=2$のとき, グラフの傾きは$a$です.
• さらにいえば, $x$がどんなときでも, グラフの傾きは$a$です.

　ここで, $y=ax+b$を微分してできた関数は

• $x=1$のとき, $y=a$
• $x=2$のとき, $y=a$
• さらにいえば, $x$がどんなときでも, $y=a$

　を満たす関数なので, 「$y=a$(定数関数)」になります.

なんとなく気持ちが理解できましたかね. しかし, この記事は微分を理解する記事ではないので未履修の方はここでさよならです. ここからは普通に$\sin x$を微分していきます.

定義に沿って計算してみると...?

　では, $\sin x$を微分の定義に沿って計算してみましょう.

$\sin x$を微分する. 定義式に当てはめると以下のようになる.
$${\lim_{h \to 0}\frac{\sin(x+h)-\sin x}{h}}$$

ここで, $\sin(x+h)$を加法定理で展開する.
$${\lim_{h \to 0}\frac{\sin x \cos h+\cos x \sin h-\sin x}{h}}$$

$\sin x$でくくり, 整理する.
$${\lim_{h \to 0}(\sin x \cdot \frac{\cos h-1}{h}+\cos x\cdot\frac{\sin h}{h})}$$
...

...

？？？？？？？？？？？？？？？？？？？？？(白目をむいている)

　ってなわけで, これ以上計算ができなさそうです. 違う形の不定形が2個もあって心が折れます.
　では, ここで不定形を処理していきましょう(鬼畜)

$\lim_{h \to 0}\frac{\sin h}{h}$の計算

　突然ですが, 下の図を考えます.

突然出てきた単位円($r=1$)

　ここで,$\triangle ABO \lt (赤色の扇型) \lt \triangle A'BO$が成り立ちます.

　では, 中心角を$\theta$(ラジアン)としてそれぞれの面積を求めましょう.

1. $\triangle ABO$の面積

　第1章, 三角関数の面積公式より$\triangle ABO=\frac{\sin\theta}{2}$

2. 赤色の扇型の面積

　第0章, 問題1(ラジアンの問題)より,$\frac{\theta}{2}$

3. $\triangle A'BO$の面積

　底辺1,高さ$\tan\theta$(第0章, 定義3の直後)より, $\triangle A'BO=\frac{\tan\theta}{2}$

　よって,$\theta \gt 0$のとき,
$${\frac{\sin\theta}{2} \lt \frac{\theta}{2} \lt \frac{\tan\theta}{2}}$$
が成り立つ.

2をかけてsinθで割ると次式を得る.
$${1 \lt \frac{\theta}{\sin\theta} \lt \cos\theta}$$

分母と分子をひっくり返して順番を左右逆にすると次式を得る.
$${\frac{1}{\cos \theta} \lt \frac{\sin\theta}{\theta} \lt 1}$$

ここで, $\theta \gt 0$だから$\theta$をプラスから$0$に近づけていく.
左も右も1に近づくから, 真ん中の$\frac{\sin\theta}{\theta}$は必ず$1$に近づく(はさみうちの定理).

よって,
$${\lim_{\theta \to +0}\frac{\sin\theta}{\theta}=1}$$

ここで,$\theta$を$-\varphi$に変えると次式を得る.
$${\lim_{-\varphi \to +0}\frac{\sin(-\varphi)}{-\varphi}=1}$$

近づけ方は$\varphi \to -0$とでき, $\sin(-\varphi)=-\sin\varphi$(図を考えれば明らか)なので次式を得る.
$${\lim_{\varphi \to -0}\frac{-\sin\varphi}{-\varphi}=1}$$
$${\lim_{\varphi \to -0}\frac{\sin\varphi}{\varphi}=1}$$

よって,$\frac{\sin h}{h}$は,$h$を正から0に近づけても負から0に近づけても$1$になると分かった.

$\lim_{h \to 0}\frac{\cos h-1}{h}$の計算

分母分子に$\cos h+1$と$h$をかけ,
$${\lim_{\theta \to 0}(\frac{\cos h-1}{h}\cdot \frac{\cos h+1}{\cos h+1} \cdot \frac{h}{h})}$$
$${\lim_{h \to 0}(\frac{\cos^2 h-1}{h^2}\cdot \frac{h}{\cos h +1})}$$

ここで, $\sin^2 h+ \cos^2 h=1$より,
$${\lim_{h \to 0}(-(\frac{\sin h}{h})^2\cdot \frac{h}{\cos h +1})}=-1^2 \cdot\frac{0}{2}=0$$

本題(微分の続き)

　$\sin x$の微分に戻ります.

$${\lim_{h \to 0}(\sin x \cdot \frac{\cos h-1}{h}+\cos x\cdot\frac{\sin h}{h})}$$

ここで, 先ほど求めた極限により, これが計算できる.

$${\sin x \cdot 0 +\cos x\cdot 1}$$

よって,$\sin x$を微分した関数は$\cos x$である.

　なんと!! 驚くべきことです!!

　sinを微分したらcosになったではありませんか!!

　では, ここでcosを微分してみてください..!!!

...

...

してみましたか?

そうなんです! cosを微分すると次のようになります!

この事実から, 驚くべきことが分かります.

実は, 三角関数を微分すると,
$${\sin x \to \cos x \to -\sin x \to -\cos x \to \sin x \to \cdots}$$

というように周期的に関数が出てくるのです!!!!!!
　幾何学から生まれた三角関数が, 解析学的にとても美しい性質をもっているところに感動を覚えます!!!

はい, じゃあ次の話に行きますね()

3-2. 三角関数のマクローリン展開

　三角関数というのは幾何学で定義された概念であって, 今まで具体値を「加法定理」を使って代数的に求めてきました.
　また, そのグラフについて, 「微分」を使って解析的にその性質を導いてきました.
　しかし, この関数はあくまでも幾何的に定義されたものです. しかし, もしも三角関数―$\sin x,\cos x, \tan x$を$x$の冪級数で表せたとしたら, どのような形になるのでしょうか...?
　この考え方が「マクローリン展開」です.

冪級数で近似する

$\sin x$が$x$の冪級数で近似できる, つまり以下の式が成り立つとしましょう.
$${\sin x \approx a_0+a_1x+a_2x^2+a_3x^3+\cdots}$$
ここで, 両辺を$k$階微分してみましょう.
$${(\sin x)^{(k)} \approx k!a_k+ {}_{k+1} \mathrm{P}_kx+{}_{k+2} \mathrm{P}_k x^2+\cdots}$$
(ただし,$f^{(k)}(x)$で, $f(x)$を$k$階微分した関数を表すこととする.)
ここで, $x=0$を代入して整理すると,
$${a_k=(\sin 0)^{(k)}\frac{1}{k!}}$$
ここで,
$(\sin 0)^{(0)}=\sin 0=0,$
$(\sin 0)^{(1)}=\cos 0=1,$
$(\sin 0)^{(2)}=-\sin 0=0,$
$(\sin 0)^{(3)}=-\cos 0=-1,$
$\cdots$
より, 次式を得る.
$${\sin x \approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}\cdots}$$
そして, じつはこの左辺と右辺は「厳密に」等しい(要証明だが, ここではしない)
$\cos x$についても同様の議論ができ, 以下の等式を得る.

　なんと! 幾何学によって定義された関数がこんなにもきれいな形をしていたのですね!!! とても数学の神秘を感じます(n回目).

　では, ここで数学のチート解法を体験してもらいましょう.

(解答)
$\sin 1=1-\frac{1}{6}+(\frac{1}{5!}-\frac{1}{7!})+(\frac{1}{9!}-\frac{1}{11!})\cdots \gt \frac{5}{6}=0.8333...$
より明らか

はい, チートです.
少なくとも高校の試験や大学入試でこれをやってはいけません()

4. 積分に使える三角関数

　積分のテクニック「置換積分」において, 変数を三角関数で置換すると変態的に解きやすくなる場合があります. ここでは, 有名な置換をいくつか紹介してみようと思います.
　積分をしっかり学習している方は見なくても大丈夫です.

1. $x=\sqrt{a}\sin \theta$

$$ \int \sqrt{a-x^2} dx=\sqrt{a}\int \left| \cos\theta \right| \cos \theta d\theta $$
定積分なら積分区間によって絶対値を外せてきれいになります！

2. $x=\sqrt{a}\tan \theta$

$$ \int \frac{1}{x^2+a}dx=\frac{1}{\sqrt{a}}\int d\theta $$
なんと被積分関数がバッサリ消えます！

3. $\tan\frac{\theta}{2}=t$

$$ \int \frac{1}{a+b\sin \theta}d\theta=\int \frac{2}{(a+b)+(a-b)t^2}dt $$
このあと, 2. を使えばもっときれいになりますね!($a-b \neq0$に限る)
$$ \int \frac{2}{(a+b)+(a-b)t^2}dt=\frac{2}{\sqrt{a^2-b^2}}\int dx $$

　本当はもっとたくさんのテクニックがあるかと思いますが, 積分をあまり学習していない人にとっては三角関数による置換積分の便利さを感じるにはこれで十分かと思います.
　今の時代, youtubeなどのコンテンツで高校の積分はマスターできちゃうので 某アンパンマン氏 等の動画を参考にすることをおすすめします.

(ほんとうにいつもわかりやすい動画をありがとうございます...!)

5. 世界一美しい数式

　巷ではこのように宣われる数式.

　オイラーの等式というものがある.
　彼の残した数多の数式, 定理, 証明の中でも特段ちやほやされている数式だ. 筆者の個人の感想としては, オイラーの等式自体よりも$\sin x$のマクローリン展開とかのほうがよっぽど美しく見えるのだが, 世間的にはそれは違うらしい(解せぬ).
　しかしながら, 初めて見た瞬間の衝撃は忘れられない. こんなことがあっていいのか. そのような思考に陥る.

　さっそく, その等式を理解するための準備に入る.

複素数とは

　実数全体の集合を$\mathbb{R}$とする. 例えば, $0 \in \mathbb{R}$だし, $-\pi \in \mathbb{R}$だ.
　突然だが, $\mathbb{R}$は「体」という代数構造をもつ. 簡単に言えば, 加減乗除ができる集合のことだ. 整数は, 割り算をすると整数で無くなる場合があるから体でない. いっぽう, 実数は, 割り算をしても必ず商は実数になるため体である(ゼロ除算を除く). これくらいの理解でいい.
　ここで, $x^2+1=0$という方程式を考える. この解は体$\mathbb{R}$の中に存在しない. そこで, この方程式の解を$\pm\sqrt{-1}$と定義する.

　では, いっぱんに$a,b \in \mathbb{R}$を用いて$a+b\sqrt{-1}$と表される数全体の集合が体であることを示そう.
　わかりやすさのためにこの体を$\mathbb{C}$と書く.
　さらに, $\mathbb{C}$は交換法則と結合法則が成り立つこととする(本当は示さないといけない).

足し算する

　$a_{1},b_{1},a_{2},b_{2}\in \mathbb{R}$とする.
　$(a_{1}+b_{1}\sqrt{-1})+(a_{2}+b_{2}\sqrt{-1})=(a_{1}+a_{2})+(b_{1}+b_{2})\sqrt{-1}$であり, $a_{1}+a_{2},b_{1}+b_{2}\in \mathbb{R}$であるからこれもまた$\mathbb{C}$の要素である.

引き算する

　足し算と同じ.

掛け算する

　$a_{1},b_{1},a_{2},b_{2}\in \mathbb{R}$とする.
　$(a_{1}+b_{1}\sqrt{-1})(a_{2}+b_{2}\sqrt{-1})=(a_{1}a_{2}-b_{1}b_{2})+(a_{1}b_{2}+a_{2}b_{1})\sqrt{-1}$であり, $a_{1}a_{2}-b_{1}b_{2}\, ,a_{1}b_{2}+a_{2}b_{1}\in \mathbb{R}$であるからこれもまた$\mathbb{C}$の要素である.

割り算する

　$a_{1},b_{1},a_{2},b_{2}\in \mathbb{R}$とする.
　$\frac{a_{1}+b_{1}\sqrt{-1}}{a_{2}+b_{2}\sqrt{-1}}=\frac{a_{1}+b_{1}\sqrt{-1}}{a_{2}+b_{2}\sqrt{-1}}\cdot \frac{a_{2}-b_{2}\sqrt{-1}}{a_{2}-b_{2}\sqrt{-1}}$ $ =\frac{(a_{1}a_{2}+b_{1}b_{2})+(-a_{1}b_{2}+a_{2}b_{1})\sqrt{-1}}{a_{2}^2+b_{2}^2}=\frac{a_{1}a_{2}+b_{1}b_{2}} {a_{2}^2+b_{2}^2}+\frac{-a_{1}b_{2}+a_{2}b_{1}}{a_{2}^2+b_{2}^2}\sqrt{-1}$
ここで, $\frac{a_{1}a_{2}+b_{1}b_{2}} {a_{2}^2+b_{2}^2},\frac{-a_{1}b_{2}+a_{2}b_{1}}{a_{2}^2+b_{2}^2}\in \mathbb{R}$であるからこれもまた$\mathbb{C}$の要素である.

　つまり, $a+b\sqrt{-1}$という形の数は四則演算が自由にできる. この$a+b\sqrt{-1}$を複素数という.

　複素数は, 実数の組$(a,b)$によって定まるため, 座標平面の点の一つ一つが一つの複素数に対応する.
　たとえば, $(1,3)\rightarrow 1+3\sqrt{-1},\, (-3,5)\rightarrow -3+5\sqrt{-1}$である.

　ここで注意を書いておく.

複素数平面

　$1$に$i$をかけると, $i$になる. $i$に$i$をかけると, $-1$になる. $-1$に$i$をかけると, $-i$になる. $-i$に$i$をかけると, $1$になる.

　これは, $i$をかけることが, 複素平面上の点を原点中心で反時計回りに$\frac{\pi}{2}$だけ回転させる動作と対応していることを示している.
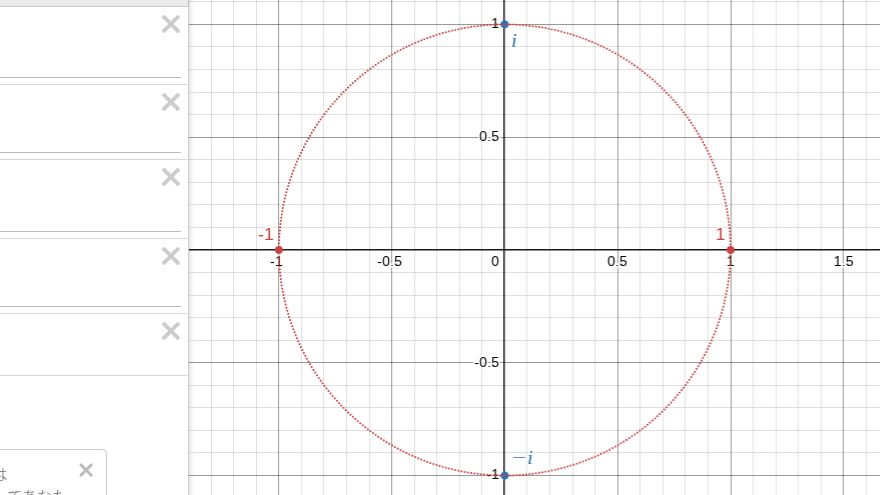編集を怠ったdesmosのスクショ

　$i$をかける動作が回転を表すということは, もっと他の複素数(たとえば$2+\sqrt{3}i$など)でも成り立つ. 気になる人は計算して確かめてほしい.

　ここで, 図6の単位円上にある複素数は, すべて$\cos\theta+i\sin\theta$という形で表される. $(1,0)$を反時計回りに$\theta$だけ回転させた点というわけだ.
　このことを気に留めながら, 以下の議論を覗いてほしい.

$e^x$のマクローリン展開

　いわゆる「指数関数」というものだ. 第3章を飛ばした人は無理して理解しなくても良いが, この関数は微分においてとてもいい働きをする. 具体的には, 微分の前後で関数の形が変化しないのです!!
　本題でないため, 結果だけ書く.

　また, 指数関数$e^x$は, 定義域が実数だったが, 指数法則を満たすように定義域を複素数へと拡張してみる.

　たとえば, $e^{2+3i}=e^2\cdot e^{3i}$が成り立つ.

　ここで,$e^{ix}$というものを考えてみよう. これ単体ではこれ以上計算ができないため, 定理14を使ってみる.

$${e^{ix}=1+\frac{ix}{1!}+\frac{(ix)^2}{2!}+\frac{(ix)^3}{3!}+\frac{(ix)^4}{4!}\cdots}$$
$i^2=-1$だから,
$${e^{ix}=1+\frac{x}{1!}i-\frac{x^2}{2!}-\frac{x^3}{3!}i+\frac{x^4}{4!}\cdots}$$
$i$がついていないものとついているものを分ける(本当は絶対収束していることを確認しないといけないがここではしないこととする).
$${e^{ix}=(1-\frac{x^2}{2!}+\frac{x^4}{4!}\cdots)+i(\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}\cdots)}$$
ここで, 三角関数のマクローリン展開を思い出してみよう. すると以下の等式を得る.
$$ {e^{ix}=\cos x+i\sin x} $$
これを「オイラーの公式」という.

　ここで, $\theta=\pi$としてみよう. すると, 以下の等式を得る.

(ちなみに, 定理/補題/系 という用語については, 某アンパンマン氏がわかりやすい動画を出しているためそれを参照してください)

　これが「世界で一番美しい数式」と呼ばれている数式です.
　確かに, 幾何学の概念の$\pi$と, 代数学の概念の$i$, 解析学の概念の$e$がきれいに結びついている, 様々な分野の数学が相互に関係し合っているということを示していると言われるとわからなくもないですが, 個人的にはこの「式」そのものよりも, それまでに必要となる証明のほうが美しいように感じます.

　あと, 余談!

　$i$は$\frac{\pi}{2}$だけ回転させた場所にあるため, $i=e^{i\frac{\pi}{2}}$であるが, これの両辺を二乗する.
　$(e^{i\frac{\pi}{2}})^i=e^{i\cdot i\frac{\pi}{2}}=e^{-\frac{\pi}{2}}$より, $i^i=e^{-\frac{\pi}{2}}$である.

　$i$とかいうわけわからない概念を$i$乗するとかいうわけわかんないことをしたら,きれいな実数になりました!!!
　なんか, あまりにもよく出来すぎているような気がします...

さいごに

　最後までご覧下さりありがとうございました！　そしてお疲れ様です。

　三角関数はこれから数学を勉強するにあたってあらゆる場面で出てきます。そして、自分で実際に使ってみて、三角関数が神ツールであることをさらに実感してほしいなと思います。

　それでは、よき数学ライフを〜

修正情報

7/11　記事投稿
7/12　$\cos$の加法定理の誤植訂正
　　　「修正情報」の作成