東大入試風の6問
はじめに
前から作っていた東大入試風の問題がある程度揃ったので、Mathlogに合うか分かりませんが、こちらで公開してみることにしました。
興味がある方は解いて見てください。略解は問題の下の方にあります。
$L$を正の実数とし,$a_{0}=0$とする。実数 $a_{n} \, (n=1,2,3, \cdots )$ を座標平面上で点$\left( a_{n-1}, \ {a_{n-1}}^{2} \right)$と点$\left( a_{n}, \ {a_{n}}^{2} \right)$の距離が$L$と等しくなり,かつ$a_{n} \gt a_{n-1}$をみたすように順次定める。
(1) $n=1,2,3, \cdots $ に対し,${a_{n}}^{2}+a_{n} \gt nL$を示せ。
(2) $\displaystyle\lim_{n \to \infty} \frac{a_{n}}{ \sqrt{n} } $を求めよ。
赤玉と白玉が$1$個ずつ入った袋$\rm{A}$と,赤玉$1$個のみが入った袋$\rm{B}$がある。
次の操作 (*) を$n$回繰り返した後,より多くの玉が入っている袋を$\rm{X}$とし,$\rm{X}$に赤玉が$2$個入っている確率を$p_{n}$,赤玉が$1$個入っている確率を$q_{n}$,赤玉が入っていない確率を$r_{n}$とする。
(*) 袋$\rm{A}$と袋$\rm{B}$にそれぞれ白玉を$1$個ずつ加える。
次に,より多くの玉が入っている方の袋から無作為に玉を$1$個選んで取り出し,もう一方の袋に移す。
(1) $p_{n+1},\ r_{n+1}$を$p_{n},\ r_{n}$を用いて表せ。
(2) $r_{n}$を求めよ。
(3) $\displaystyle\lim_{n \to \infty} p_{n}, \ \lim_{n \to \infty} q_{n},\ \lim_{n \to \infty} r_{n} $を求めよ。
$k$を正の実数とする。次の関数$f(x)$を考える。
$$ \displaystyle f(x)= \frac{\log (x^2+k) }{x} \quad (x \gt 0) $$
(1) $f(x)$ が極大値をちょうど$1$つ持つような$k$の条件を求めよ。
(2) $k$が(1)の条件をみたすとき,$f(x)$は$x=\alpha$で極大値$f(\alpha)$をとるとする。
このとき,不等式
$$ \sqrt{e-k} \lt \alpha \lt \sqrt{e^2-k} $$
$$ \frac{2}{e} \lt f(\alpha) \lt \sqrt{\frac{2}{e}} $$
を示せ。ただし,$e$は自然対数の底である。
複素数平面上の点$\rm{P(1)}$を中心とする半径$1$の円周上に相異なる$2$点$\rm{A}(\alpha),\ \rm{B}(\beta)$があり,$\rm{P}$を通り虚軸に平行な直線上に点$\rm{C(\gamma)}$がある。3点$\rm{A,\ B,\ C}$が$\alpha i+\beta i + \gamma =0$をみたすように動くとき,以下の問いに答えよ。ただし,$i$は虚数単位である。
(1) $\gamma$の虚部がとりうる範囲を求めよ。
(2) $\triangle \rm{ABC}$の外心$\rm{O}(\omega)$の軌跡を図示せよ。
$m$を正の整数,$n$を$2$以上の整数とする。正の整数の組$(a_1,\ a_2,\ \cdots,\ a_{n})$が
$$ m+a_1+a_1 a_2+a_1 a_2 a_3+ \cdots +a_1 a_2 \cdots a_{n-1}=a_1 a_2 \cdots a_n $$
をみたすとき,$\displaystyle \sum_{k=1}^{n} a_{k} $ のとりうる最大値を$M$とする。
(1) $n=2$のとき,$M$を$m$で表せ。
(2) $M$を$n,\ m$で表せ。
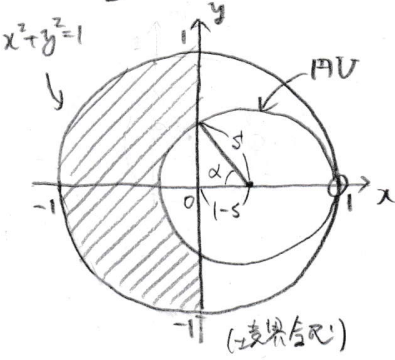
座標空間上に点$\rm{A}(0,\ 0,\ 1),\ \rm{B}(1,\ 0,\ 0)$をとる。点$\rm{P}$は$xy$平面上の原点を中心とする半径$1$の円周上を動き,点$\rm{Q}$は線分$\rm{BP}$上を動く (ただし$\rm{P} \neq \rm{B}, \rm{Q} \neq \rm{B}$とする)。線分$\rm{AQ}$上に$\displaystyle \rm{\frac{BQ}{BP}=\frac{QR}{AQ}} $をみたすように点$\rm{R}$をとり,線分$\rm{QR}$が通過する領域を$D$とする。ただし,線分はいずれも端点を含むものとする。
(1) $s$ を$0\lt s\lt 1$をみたす定数とする。線分$\rm{QR}$が平面$z=s$と共有点をもつような点$\rm{Q}$の範囲を$xy$平面上に図示せよ。
(2) $\displaystyle\frac{1}{2} \leqq t \leqq 1$とする。実数$\alpha,\ u$が
$$ \cos \alpha= \frac{1-t}{t} \ (0 \leqq \alpha \leqq \frac{\pi}{2}),\quad u=\alpha - \frac{1}{2} \sin 2\alpha $$
をみたすとき,$\displaystyle \frac{du}{dt}$を$t$で表せ。
(3) $D$の$x\leqq 0$の部分の体積を求めよ。
*
*
*
*
*
* 以下略解
*
*
*
*
*
第一問
解けない漸化式の極限。思いつけば一瞬だが…
(1) ${\rm{A_n}}( a_{n}, \ {a_{n}}^{2} )$と${\rm{B_n}}( a_{n}, \ {a_{n-1}}^{2} )$と定めると,直角三角形$\rm{A_{k-1} A_k B_k}$について(斜辺の長さ)$\lt$(他の2辺の長さの和)より
$$ ({a_{k}}^{2}-{a_{k-1}}^{2})+(a_k - a_{k-1})\gt L$$
これを$k=1,\ 2,\ \cdots ,\ n$ に対し辺々加えて題意の式を得る。
(2) (1)より $\displaystyle \frac{a_n}{\sqrt{n}} \gt \sqrt{L+ \frac{1}{4n} }- \frac{1}{2 \sqrt{n} }$
また直角三角形$\rm{A_{k-1} A_k B_k}$について(斜辺の長さ)$\gt$($y$軸に平行な辺の長さ)より$L \gt {a_{k}}^{2}-{a_{k-1}}^{2}$
これを$k=1,\ 2,\ \cdots ,\ n$ に対し辺々加えて,$nL \gt {a_{n}}^{2}$ すなわち$\displaystyle \sqrt{L} \gt \frac{a_n}{\sqrt{n}}$を得る。
以上から,はさみうちの原理を用いて $\displaystyle\lim_{n \to \infty} \frac{a_{n}}{ \sqrt{n} }= \sqrt{L}$
第二問
確率漸化式。こちらは解ける漸化式。
(1) $n+1$回目の操作中,両方の袋に白玉を入れた時点を考える。次に袋$X$から$Y$へと玉が移るとする。
[i] $Y$が白玉のみになるのは,以下の場合だけなので
$\overbrace{\underbrace{ \boxed{赤} \boxed{赤}\underbrace{\boxed{白}\boxed{白} \cdots \boxed{白}}_{n+1個}}_{n+3個}}^{X} \rightarrow_{白} \overbrace{\underbrace{ \boxed{白} \cdots \boxed{白}}_{n+2個}}^{Y}$ $\displaystyle r_{n+1}= \frac{n+1}{n+3} p_n \quad \cdots ①$
[ii] $Y$が赤玉のみになる場合は,以下の排反な$2$パターンがあるので
$\overbrace{\underbrace{ \boxed{赤} \underbrace{\boxed{白} \cdots \boxed{白}}_{n+2個}}_{n+3個}}^{X} \rightarrow_{赤} \overbrace{\underbrace{ \boxed{赤}\boxed{白} \cdots \boxed{白}}_{n+2個}}^{Y}$ $\overbrace{\underbrace{ \boxed{白} \cdots \boxed{白}}_{n+3個}}^{X} \rightarrow_{白} \overbrace{\underbrace{ \boxed{赤}\boxed{赤}\boxed{白} \cdots \boxed{白}}_{n+2個}}^{Y}$
$\displaystyle p_{n+1}= \frac{1}{n+3}q_n+r_n $
$p_n+q_n+r_n=1$より,$\displaystyle p_{n+1}= -\frac{1}{n+3}p_n+\frac{n+2}{n+3}r_n+\frac{1}{n+3} \quad \cdots ②$
(2) ①$-$②を変形して,$\displaystyle (n+3)(r_{n+1}-p_{n+1})+\frac{1}{2}=-\lbrace (n+2)(r_{n}-p_{n})+\frac{1}{2} \rbrace$
$\displaystyle p_1=\frac{1}{3},\ r_1=0$より $\displaystyle (n+2)(r_{n}-p_{n})+\frac{1}{2}$は初項$\displaystyle -\frac{1}{2}$,公比$-1$の等比級数であるから,$\displaystyle r_{n}-p_{n}=\frac{(-1)^n-1}{2(n+2)}$
①を用いて変形して,$\displaystyle (n+3)(n+2)r_{n+1}=(n+2)(n+1)r_n+(n+1)\frac{1-(-1)^n}{2}$
$\displaystyle\therefore r_n=\frac{1}{(n+1)(n+2)} \underbrace{\sum_{k=1}^{n-1}(k+1)\frac{1-(-1)^k}{2}}_{a_nとする} \quad (n \geqq 2)$
$n=2m+1 \ (m \in \mathbb{N} )$のとき,$\displaystyle a_n=\sum_{k=1}^{m}2k=m(m+1)=\frac{n^2-1}{4}$
$n=2m \ (m \in \mathbb{N} )$のとき,$\displaystyle a_n=a_{2m+1}=m(m+1)=\frac{n(n+2)}{4}$
以上より $\displaystyle r_n= \begin{eqnarray}
\left\{
\begin{array}{l}
\frac{n-1}{4(n+2)} \quad (n \rm{が奇数のとき}) \\
\frac{n}{4(n+1)} \quad (n \rm{が偶数のとき})
\end{array}
\right.
\end{eqnarray} $ これは$n=1$でも成立。
(3) (2)より$n \to \infty$で$r_n$は偶奇それぞれ同じ値に収束するので,$\displaystyle\lim_{n \to \infty} r_n = \frac{1}{4}$
①より $\displaystyle\lim_{n \to \infty} p_n = \lim_{n \to \infty} \frac{n+3}{n+1}r_{n+1} = \frac{1}{4}$
余事象より $\displaystyle\lim_{n \to \infty} q_n = \displaystyle\lim_{n \to \infty} (1-p_n-r_n) =\frac{1}{2}$
第三問
数Ⅲ微分法。
(1) $\displaystyle f^{\prime}(x)= \frac{2x^2-(x^2+k)\log(x^2+k)}{x^2(x^2+k)} $ の分母は常に正であり,分子を$g(x)$とすると
$g^{\prime}(x)= 2x \lbrace 1-\log(x^2+k) \rbrace$である。以下便宜的に$g(0)=-k\log{k}$を考える。
$k \geqq e$のとき,$g^{\prime}(x) \lt 0$ かつ $g(0) \lt 0$ より$g(x) \lt 0$ であるから,$f(x)$ は単調減少し,極値をもたない。
$0 \lt k \lt e$ のとき,$g(x)$は$x=\sqrt{e-k}$ で極大値$e-2k$ をとり,増加→減少に転じる。題意の条件をみたすには$g(x)$が正→負へと変化する箇所がちょうど$1$箇所あればよく,$g(\sqrt{e^2-k})=-2k<0$ より$g(\sqrt{e-k})=e-2k>0$ であれば必要十分。
以上より答えは$\displaystyle 0 \lt k \lt \frac{e}{2}$。
(2) (1)より$\alpha$は開区間$(\sqrt{e-k},\ \sqrt{e^2-k})$ にあるので最初の不等式は成立。変形して$e \lt \alpha ^2+k \lt e^2$を得る。
$g(\alpha)=2\alpha ^2-(\alpha ^2+k)\log(\alpha ^2+k)=0$ を変形して,$\displaystyle \frac{2\log(\alpha ^2+k)}{\alpha ^2 + k}= (\frac{2\alpha}{\alpha ^2 + k})^2 $ を得る。
また$\displaystyle f(\alpha)=\frac{\log(\alpha ^2+k)}{\alpha}=\frac{2\alpha}{\alpha ^2+k}$ と変形でき,$\displaystyle h(x)=\frac{2\log x}{x}$ とおくと,$\displaystyle {f(\alpha)}^2=\frac{2\log(\alpha ^2+k)}{\alpha ^2 + k}=h(\alpha ^2+k) $ となる。
$h(x)$ を微分して増減表をかき,開区間$(e,\ e^2)$ における値の範囲を調べることにより,$\displaystyle \frac{4}{e^2} \lt {f(\alpha)}^2 \lt \frac{2}{e}$が示され,$f(\alpha)\gt 0$より二番目の不等式が示される。
第四問
複素数平面のテクニックは殆ど使わない。
(1) $\gamma=1+ai$ ($a$は実数) とおくと,線分$\rm{AB}$ の中点$\rm{M}$は$\displaystyle \frac{\alpha+\beta}{2}=\frac{i\gamma}{2}=\frac{i}{2}-\frac{a}{2}$となり,$\rm{M}$は虚部が$\displaystyle \frac{i}{2}$の直線上にある。
相異なる $\alpha,\ \beta$ が存在するには,$\rm{M}$が題意の円 ($ \Gamma $とする) の内部にあることが必要。このとき$\rm{AM=BM}$ となるには,対称性より$\rm{PM \perp AB}$となるように$\alpha,\ \beta$をとることが必要であり,これは$\rm{M}$が$ \Gamma $内なら常に可能である。
以上より求める$a$の条件は,$\rm{M}$が$ \Gamma $ 内にある範囲であり,$-2- \sqrt{3} \lt a \lt \sqrt{3} -2$。
(2) $\rm{O}$は直線$\rm{MP}$上にあり,点$\rm{Q(2)}$をとって$ \angle \rm{QPM}= \theta $ とする。
$\rm{M}$の虚部$\displaystyle =\frac{1}{2}$,直角三角形$\rm{APM}$,および$\rm{O}$が線分$\rm{AP}$の二等分線上にあることに注意して,
$\displaystyle \rm{MP}\sin \theta= \frac{1}{2}$, $\displaystyle \rm{MP}=\cos \angle APM$, $\displaystyle \rm{OP}\cos \angle APM= \frac{1}{2}$ が得られ,$\rm{OP}=\sin \theta$ と分かる。
$\displaystyle\omega=(1+\rm{OP}\cos\theta)+(\rm{OP}\sin\theta)\textit{i}=(1+\frac{1}{2}\sin 2\theta)+\frac{1-\cos 2\theta}{2}\textit{i}$
$\displaystyle \frac{\pi}{6} \lt \theta \lt \frac{5\pi}{6}$ より,$\rm{O}$の軌跡は中心$\displaystyle 1+\frac{i}{2}$,半径$\displaystyle \frac{1}{2}$の円の虚部が$\displaystyle \frac{1}{4}$ より大きい部分 (図示略)。
第五問
帰納法で解ける整数問題。
$\displaystyle S=\sum_{k=0}^{n} a_{k}$とする。
(1) $m=a_1 (a_2-1)$ より,$a_1$は$m$の約数であるから,$1 \leqq a_1 \leqq m$である。
$\displaystyle f(x)=x+\frac{m}{x} \ (1 \leqq x \leqq m)$ を微分して増減を調べると,$x=1,m$のとき最大値$m+1$をとる ($m=1$でも成立)。
$\displaystyle\therefore S=a_1+a_2=a_1+\frac{m}{a_1}+1$の最大値は$M=m+2$である。
(2) $S \leqq m+2(n-1) \ \cdots(☆)$が任意の$m$に対し成り立つことを,各$n$についての数学的帰納法で示す。
$n=2$のとき,(1)より成立。$n=k$のとき成立すると仮定し,$n=k+1$のときを考える。
与条件より $\displaystyle(\frac{m}{a_1}+1) +a_2+a_2 a_3 + \cdots +a_2 a_3 \cdots a_{k}= a_2 a_3 \cdots a_{k+1}$であり,
仮定において,$m$を$\displaystyle\frac{m}{a_1}+1$,$(a_1,\ \cdots ,\ a_k)を(a_2,\ \cdots ,\ a_{k+1})$として適用して
$\displaystyle S=a_1+\sum_{i=2}^{k} a_{i} \leqq a_1 + \frac{m}{a_1}+1+2(k-1)$
$\displaystyle \frac{m}{a_1}$が正の整数より$1 \leqq a_1 \leqq m$であり,(1)の$f(x)$の結果から$S \leqq m+2k$となり,$n=k+1$のときも成立。
$\therefore$(☆)は成立し,等号は$a_1=a_2=\cdots=a_{n-1}=1,\ a_n=m+n-1$のとき成り立つので,$M=m+2(n-1)$である。
第六問
かなり面倒な求積問題。
(1) 点${\rm{Q}}(x,y,0),\ {\rm{C}}(-1,0,0),\ {\rm{O}}(0,0,0)$ とする $(-1\leqq x \lt 1)$。
${\rm{BP}:\rm{BC}}=(1-x):{\rm{BQ}}$より,$\displaystyle \frac{\rm{QR}}{\rm{AQ}}=\frac{\rm{BQ}}{\rm{BP}}=\frac{\rm{BQ}^2}{2(1-x)}=\frac{(x-1)^2+y^2}{2(1-x)}$
$\rm{QR}$が平面$z=s$と共有点をもつ条件は$\displaystyle s \leqq \frac{\rm{QR}}{\rm{AQ}}$より,$\lbrace x-(1-s) \rbrace ^2 +y^2 \geqq s^2$
$\therefore \rm{Q}$の条件は,「原点を中心とする半径$1$の円の周および内部」かつ「点$(1-s,\ 0)$を中心とする半径$s$の円の周および外部」 (ただし点$\rm{B}$を除く) (図示略)
(2) $\displaystyle \frac{du}{d\alpha}=2\sin ^2\alpha$,$\sin\alpha \geqq 0$より$\displaystyle \sin\alpha=\frac{\sqrt{2t-1} }{t}$
$\displaystyle \cos \alpha= \frac{1-t}{t} $の両辺を$t$で微分して,$\displaystyle \sin\alpha \cdot \frac{d\alpha}{dt}=\frac{1}{t^2}$
以上より,$\displaystyle \frac{du}{dt}=\frac{du}{d\alpha}\cdot \frac{d\alpha}{dt}=\frac{2\sqrt{2t-1}}{t^3}$
(3) $\rm{Q}$が (1) かつ$x \leqq 0$の範囲を動く場合を考えればよく,この範囲の面積を$Y(s)$とする。
相似より,求める領域の$z=s$における断面積$X(s)$は$X(s)=(1-s)^2Y(s)$である。
[i] $\displaystyle 0\leqq s\leqq \frac{1}{2}$のとき $\rm{Q}$は半径$1$の半円の周および内部を動くので,$\displaystyle X(s)=\frac{\pi}{2}(1-s)^2$
[ii] $\displaystyle \frac{1}{2}\leqq s\leqq 1$のとき
$\rm{Q}$が動く領域の面積は図より,$\displaystyle \frac{\pi}{2}-s^2(\alpha-\frac{1}{2}\sin 2\alpha) \quad ({\rm{ただし}}\cos\alpha=\frac{1-s}{s},\ 0 \leqq \alpha\leqq \frac{\pi}{2})$
$\displaystyle \therefore X(s)=\frac{\pi}{2}(1-s)^2-s^2(1-s)^2(\alpha-\frac{1}{2}\sin 2\alpha)$
[i][ii]より求める面積$V$は,
$\displaystyle V= \underbrace{\frac{\pi}{2}\int_{0}^{1}(1-s)^2ds}_{①とする}-\underbrace{ \int_{\frac{1}{2}}^{1}s^2(1-s)^2(\alpha-\frac{1}{2}\sin 2\alpha)ds}_{②とする}$
(2)で$t=s$とすると$\displaystyle (\alpha-\frac{1}{2}\sin 2\alpha)\frac{d}{ds}=\frac{2\sqrt{2s-1}}{s^3}$であり,部分積分を用いて,
②$\displaystyle = \int_{\frac{1}{2}}^{1}(\frac{1}{5}s^5-\frac{1}{2}s^4+\frac{1}{3}s^3)^{\prime}(\alpha-\frac{1}{2}\sin 2\alpha)ds$
$\displaystyle = \underbrace{ \biggl \lbrack (\frac{1}{5}s^5-\frac{1}{2}s^4+\frac{1}{3}s^3)(\alpha-\frac{1}{2}\sin 2\alpha) \biggr\rbrack ^{1}_{\frac{1}{2}}}_{③とする} -\underbrace{\int_{\frac{1}{2}}^{1}(\frac{1}{5}s^5-\frac{1}{2}s^4+\frac{1}{3}s^3)\frac{2\sqrt{2s-1}}{s^3}ds}_{④とする}$
④$\displaystyle =2\int_{\frac{1}{2}}^{1}(\frac{1}{5}s^2-\frac{1}{2}s+\frac{1}{3})\sqrt{2s-1}ds$
$\displaystyle =\int_{\frac{1}{2}}^{1} \lbrace \frac{1}{10}(2s-1)^{\frac{5}{2}}-\frac{3}{10}(2s-1)^{\frac{3}{2}}+\frac{4}{15}(2s-1)^{\frac{1}{2}} \rbrace ds=\frac{68}{1575} $
①$\displaystyle =\frac{\pi}{6}$,③$\displaystyle =\frac{\pi}{60}$より,$\displaystyle V= \frac{3 \pi }{20}+\frac{68}{1575}$
ChatGPT o3-miniに解かせてみた
配点を下記のように定め,ChatGPT o3-miniに解かせたところ,以下のような結果となり、合計点は51/120点となった。
1(1)◯ (2)△2点 2(1)◯ (2)☓ (3)☓ 3(1)△3点 (2)☓
4(1)◯(2)☓ 5(1)◯(2)△6点 6(1)△4点(2)◯(3)☓
上位モデルだともっと解けるのかもしれない。
第一問 (1) 8点 (2) 12点
第二問 (1) 8点 (2) 8点 (3) 4点
第三問 (1) 10点 (2) 10点 (配点は後半の不等式のみ,前半は(1)のヒント)
第四問 (1) 10点 (2) 10点
第五問 (1) 6点 (2) 14点
第六問 (1) 6点 (2) 4点 (3) 10点
詳細:
1(2)は近似計算をしてきたので,会話ではさみうちに誘導してみたが,今度は誤った議論となった。
2(1)は$p_{n+1}$は$q_{n}$を消してくれなかったが許した。
(2)の漸化式は解けず、(3)はシミュレーションで答えをだしてきた。
3(1)は$g^{\prime}(x)$に相当する箇所の計算を誤った。
(2)の後半は$\displaystyle \frac{(\log x)^2}{x-k} $の増減を区間$(e,\ e^2)$で調べることに帰着させ,"容易に示せる"と一言で片付けたが,おそらく容易でない。
4(2)は長考の末,三次の代数曲線と答えた。
5(2)は答えは予想できていた。すごくセンスの良さそうな証明を出してきたが,よく読むとハルシネーションだった。
6(1)は境界のみ回答したので減点した。
(3)は立式も無理だったが、積分式を与えると近似計算で答の値を出すことはできた。