初記事です。
どうも初めまして。haaaaaaaと申します。
普段は数学のいろんな分野を広く浅くいじりまくってます。
私はMathlogにいる他の皆さんほど頭は良くない方ですので御粗末な物しか書けないと思います。
記事はいい感じの結果が得られたらゆるくまったり書いていこうかと思います。
自己紹介
(情報は全て2025年8月時点のものです)
- 競技数学、大学数学をやっている公立中3
- (競技数学の中では)整数、組み合わせが好き
- 幾何も最近興味を持ち始めている(ただし出来るとは言っていない)
- 代数は苦手
- 競技数学以外では積分、級数が好き
(数学関係ないけど)音ゲーマー
折角なので自作問題を
自己紹介だけで終わらせるのも何なので自作問題を一問だけ置いていこうかなと思います
(三角関数などを用いると驚くほど簡単に解けてしまうので出来れば初等幾何で解く方法も考えてみてください)
$AB = 5,BC = 3,\angle ABC = 120 \degree $である三角形$ABC$の外接円と$\angle B$の二等分線との交点を$D$とする。このとき四角形$ABCD$の面積を求めよ。
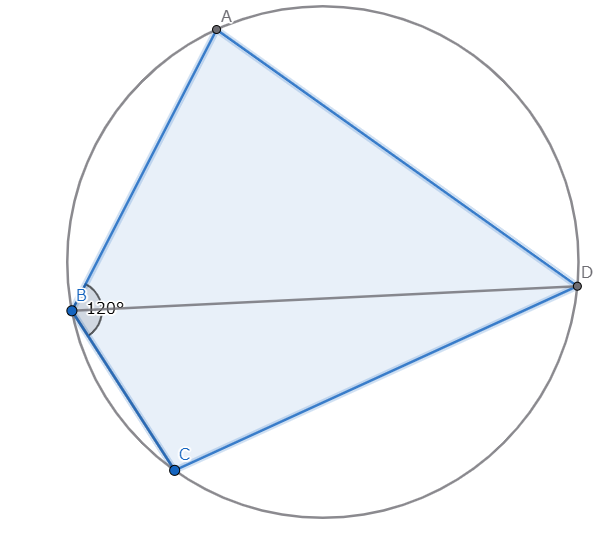 問題
問題
解説
この先にこの問題の解説があります。自力で考えたい人は戻って考えることをおすすめします。
ネタバレ注意
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
円に内接する四角形の性質により$\angle ADC = 60 \degree$,
$\angle ABD$と$\angle CBD$が$\angle CBA$の二等分線になっているので$\angle ACD = \angle CAD = 60\degree$になるので$ \triangle ACD$は正三角形になりますね。
なので$CA = AD$なので$\triangle ABC \equiv \triangle DEA$となるように点Eを取ることができます。
ここで、$\angle AED + \angle ACD = \angle CBA + \angle ACD = 120\degree + 60\degree = 180\degree$なので点$E$は四点$A,B,C,D$と同じ円上にあります。
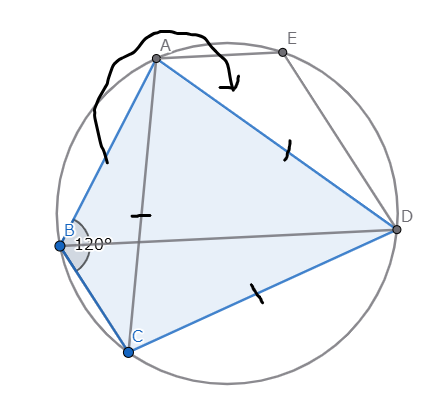 線書くの下手くそだなおい
線書くの下手くそだなおい
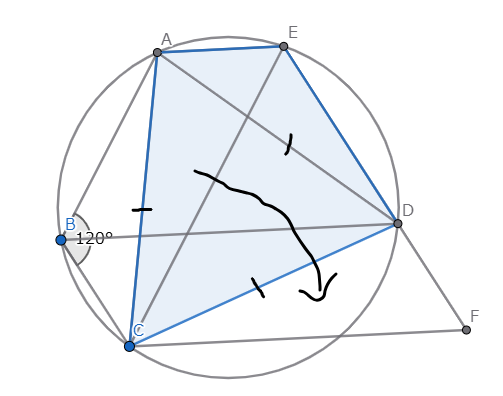
ここで、$\triangle AEC$を時計回りに$60\degree$回転させます。
$\triangle ACD$は正三角形なので、点$A$は点$D$に移り、点Eの移動先を点Fとします。
円に内接する四角形の性質より、$\angle EDF = \angle FDC + \angle CDE = \angle EAC + \angle CDE = 180\degree$なので
$E,D,F$は同一直線上にあります。
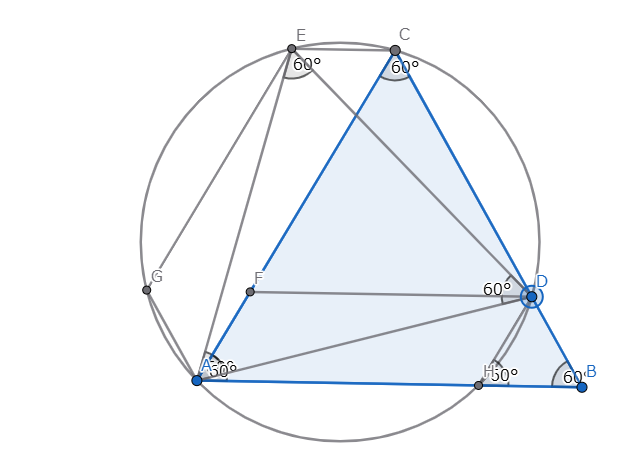
円周角の定理より$\angle ECF = \angle AEC = \angle ADC = 60\degree,\angle FEC = \angle DAC = 60\degree$なので$\triangle ECF$は正三角形になります。
ここで、この正三角形の一辺の長さを考えましょう。
$FE = FD + DE = EA + DE = BC + AB = 3 + 5 = 8$なので、正三角形$ECF$の一辺の長さは8です。
EからCFに垂線EHを引きます。
$\triangle ECF$は正三角形なので三角形$\triangle ECH$は$30\degree,60\degree,90\degree$の直角三角形になるので、$EH = 4\sqrt{3} $になります。
よって、$\triangle ECF = 1/2 \times 8 \times 4\sqrt{3} = 16\sqrt{3}$ になります。
四角形$ABCD = $ 四角形$ACDE$ = $\triangle ECF$なので、求めるべき値は$16\sqrt{3}$です!
おわりに
読みずらい部分も多々あったかもしれませんが、最後まで読んでいただきありがとうございます。やる気があっていい結果がでれば他の記事も書いていこうと思うのでよろしくお願いします。あと自作問題の解答の不備や指摘もあったら教えてください