円周率πはどこへ消えた?
円絡みの問題で求まる面積から消える$π$について
わかりません。
問題
$xyz$空間において、
$x^2+y^2=1,z\gt0,x\lt0,z\lt-x$を満たす下図のような図形の面積$S$を求めよ。
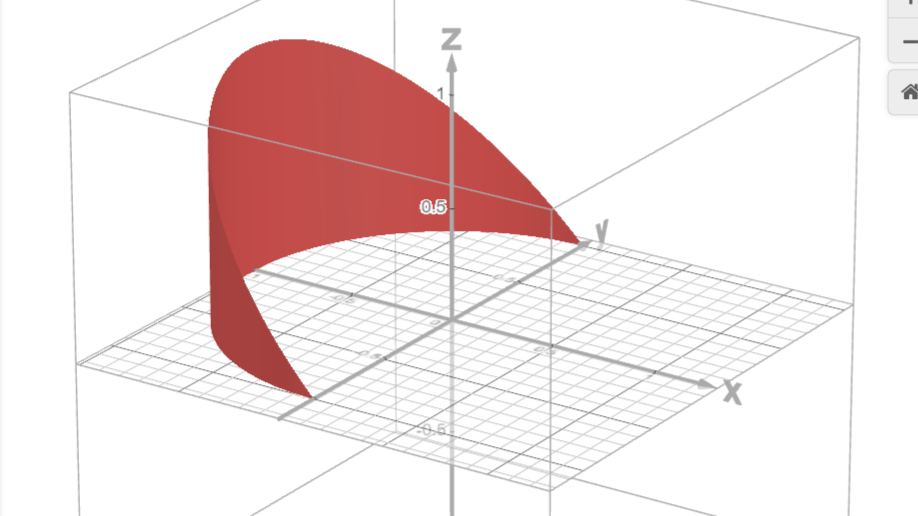 Cuttube/Desmsos
Cuttube/Desmsos
どのような求め方をしても良いのですが、一例として
$ S=\int_0^πsinθ dθ=2$
なんと面積に$π$が現れず整数で答えが出てきました。
どうしてでしょうか?直感的にはわかりません。
切られて取り除かれた方の筒の体積は$2π-2$となり、
これもまた、奇妙です。$π$の要素を押し付けた感じです。
縦方向に一般化してみる
$arcsinx$は$sinx$の定義域が$-\frac{π}2\le x\le\frac{π}2$の逆関数である。
さっきの図に対して、下と上の範囲を決めその面積を求める
$-1\leα\leβ\le1$
$S_{α,β}=-2\sqrt{1-β^2}+πβ-2β\arcsinβ+2\sqrt{1-α^2}-πα+2α\arcsinα$
普通に積分しました。
さっきの問題に適用すると
$α=0,β=1$で
$S_{0,1}$
$=-2\sqrt{1-1^2}+π-2\arcsin1+2\sqrt{1-0^2}-0π+20\arcsin0$
$=π-2・\frac{π}2+2=2$
と合ってます。
$β=1$の代入部分だけで$π$が打ち消しあい、値が$0$に。
$α=0$の代入で、$π$の出現する可能性が高い項は消え、$2$に。
$α$や$β$が$(0,1)$以外の$sin$の有名角の値で、答えに$π$成分が出ないものは無さそうです。
似た話(ヒポクラテスの三日月)
円絡みなのに$π$が消えることで有名な図形です。
斜線の面積は直角三角形の面積と等しい。
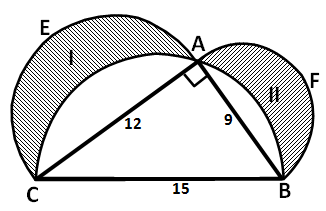 moon
moon
これは直感的に、$12^2+9^2=15^2$から察するように$π$同士が打ち消しあってる感じは伝わってくるのですが、さっきの問題はあまりピンときません。
最後に
読んで頂きありがとうございました。
なんとなく、平面図形と違って立体で積分して面積を求める過程が感覚的に身についていないから理解するのが難しいような気がします。納得のできる説明を自分でも模索中です。
「そんなの当たり前じゃん」って思ってる方が居ましたらご教授お願いいたします。
