レスターの定理の垂重円を用いた証明

重心,垂心をそれぞれ$G,H$とすると,$\measuredangle HD'G=\measuredangle HE'G=\measuredangle HF'G=\measuredangle HQ_AG=90°$より，六点$H,G,D',E',F',Q_A$は同一円周上にある.よって,角度追跡から三角形$ABC$と三角形$D'E'F'$は相似.したがって,$BC,E'F'$の中点をそれぞれ$M,M'$とすると,$\measuredangle E'M'D'=\measuredangle AMD=\measuredangle AGD'=\measuredangle Q_AF'D'$.よって四角形$D'E'Q_AF'$は調和四角形であるから,$D'E':D'F'=E'Q_A:F'Q_A$.さらに,$D'E':D'F'=AB:AC=E'A:F'A$であるので三角形$AD'Q_A$の外接円は$E',F'$におけるアポロニウスの円である. 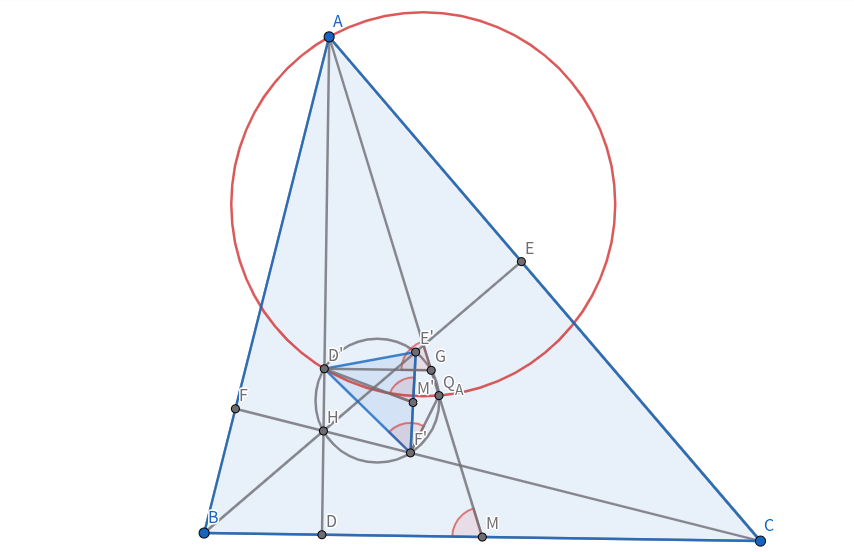補題1

$A$-共役反転で,$X$の反転先を$X^*$とする.このとき,$B^*=C,C^*=B,Q_A^*$は三角形$ABC$の外接円における$BC$の極となる.フェルマー点の定義から,$\measuredangle AF_1B=\measuredangle CF_1A=\measuredangle BF_2A=\measuredangle AF_2C$.よって,$\measuredangle ACF_1^*=\measuredangle F_1^*BA=\measuredangle F_2^*CA=\measuredangle ABF_2^*$.$BF_1^*$と$CF_2$の交点を$I$,$CF_1^*$と$BF_2^*$の交点を$J$とすると,$\measuredangle ACJ=\measuredangle ACF_1^*=\measuredangle ABF_2^*=\measuredangle ABJ$,$\measuredangle IBA=\measuredangle ICA$.したがって,五点$A,B,C,I,J$は同一円周上にある.よって,六角形$BBICCJ$にパスカルの定理を適用することで,三点$F_1^*,F_2^*,Q_A^*$は同一直線上にあることがわかる.
三角形$ABC$の外心を$O$,$O$に関して$A$と対称な点を$A'$とする.
$\measuredangle AIJ=\measuredangle ACJ=\measuredangle IBA=\measuredangle IJA$,$3\measuredangle AIJ=3\measuredangle ACJ=3\measuredangle ACF_1^*=3\measuredangle AF_2^*B=0°$より,$\measuredangle JAI=-2\measuredangle AIJ=\measuredangle AIJ$.よって,三角形$AIJ$は正三角形である.したがって,$IJ$は$A'O$の垂直二等分線で,$D'^*$は$A'$に関して$O$と対称な点であるから,$D'^*$は三角形$ABC$の外接円における$IJ$の極.よって,六角形$BIICJJ$にパスカルの定理を適用することで,三点$F_1^*,F_2^*,D'^*$が同一直線上にあることがわかる.したがって四点$F_1^*,F_2^*,Q_A^*,D'^*$が同一直線上にあるので,五点$A,D',Q_A,F_1,F_2$は同一円周上にある.また,$I$で射影することで$F_2^*,Q_A^*,F_1^*,D'^*$は調和点列をなすことがわかるので,四角形$F_1D'F_2Q_A$は調和四角形である. 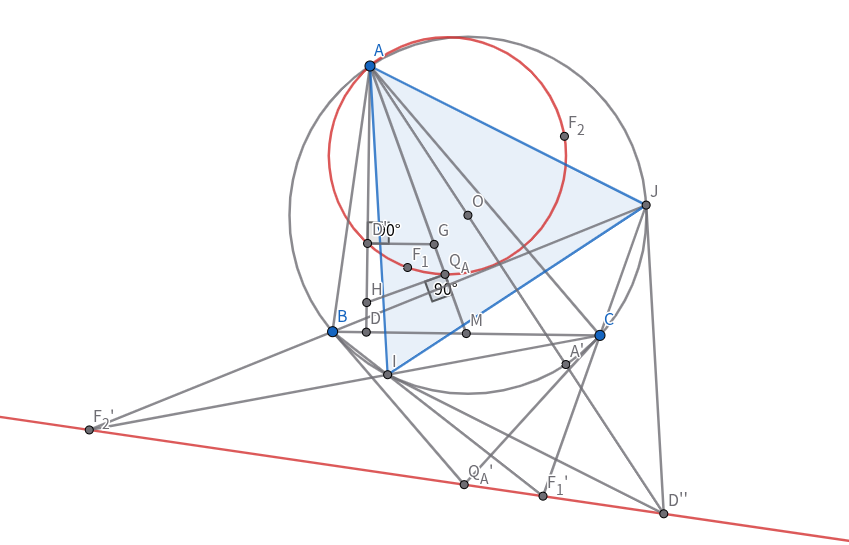補題2

補題1より,三角形$D'E'F'$の外接円と三角形$AD'Q_A$の外接円は直交するため,三角形$AD'Q_A$の外接円における$D',Q_A$の接線の交点は三角形$D'E'F'$の外心($HG$の中点)であり,この点を$O'$とする.補題2より$F_1F_2$は$O'$を通る.よって,$O'F_1×O'F_2=O'G^2$.また,四点$H,N,G,O$は調和点列を成すから,$O'G^2=O'N×O'O$.よって,$O'F_1×O'F_2=O'N×O'O$.したがって,四点$O,N,F_1,F_2$は同一円周上にある.