競技数学解説

OMC対策（G分野：垂心に関する知識）

垂心,OMC,競技数学

本記事の前提知識

　垂心を知っていれば十分である．
　なお，垂心に関する構図は数多くあると思うが，本記事では「水レートを目指すならまずはこのくらい」というものだけ扱っている．

垂心の基本

　まず，次の$2$つは最も基本的なものである．

性質１．共円について

　点$H$は$△ABC$の垂心である．
　このとき，共円である$4$点の組がいくつか存在する（例：$(A,F,H,E)$は共円である）．　
　

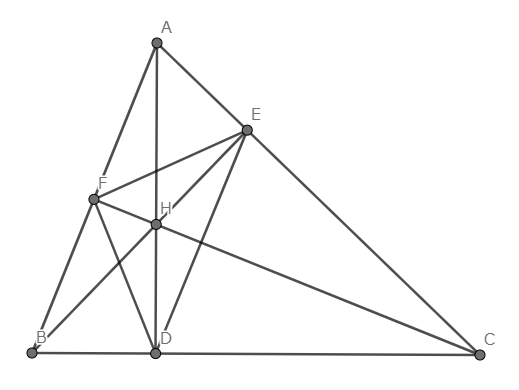
（問題）$(A,F,H,E)$が共円であることを示せ．また，そのような$4$点の組を，図からできるだけ多く発見せよ．

答え

　$\angle AFH+\angle AEH=180°$から従う．
　他に$(B,D,H,F),(C,E,H,D),(A,B,D,E),(B,C,E,F),(C,A,F,D)$も共円である．

性質２．角度について

　図1中の，線分と線分によってできる全ての角度は，$\angle A, \angle B, \angle C$のみを使って表すことができる．

（問題）実際に確かめよ．

ヒント

　頂点$A,B,C$の周りの角は，全て$90°-\angle X$という形をしている．
　頂点$D,E,F$の周りの角については，性質１を用いればよい（円周角の定理を用いよ）．

垂心に関する基礎知識

　「基礎」と書いてはみたが，競技数学における基礎知識である．受験数学でここまで求められることはまずないだろう．

垂心と外接円１

　$△ABC$の垂心，外心をそれぞれ$H,O$とする．$BC$の中点を$M$，$AA'$が円$O$の直径となるような点を$A'$とする．$AH$と線分$BC$，$A$を含まない方の円弧$BC$との交点をそれぞれ$D,H'$とする．このとき

点$H,H'$は直線$BC$について対称な位置にある
点$H,A'$は点$M$について対称な位置にある
点$A',H'$は直線$OM$について対称な位置にある

　証明は角度追跡でできる．

垂心と外接円２

　$△ABC$の垂心，外心をそれぞれ$H,O$とし，$OA=R$とする．
　このとき$AH=2R \cos A,BH=2R \cos B, CH=2R \cos C$が成り立つ．

　証明は三角比の定義に従って計算すればよい．もちろん正弦定理も使う．

Euler線（オイラー線）

　$△ABC$の外心，重心，垂心をそれぞれ$O,G,H$とする．これらの$3$点はこの順に一直線上に並び，これをEuler線という．$OG:GH=1:2$である．

　証明は例えば高校数学の美しい物語を参照．

　まずはここまで知っておけばよいと思うが，追加でもう一つ挙げるなら九点円だろうか．

九点円（フォイエルバッハ円）

　$△ABC$の垂心，外心をそれぞれ$H,O$とする．次の$9$点は同一円周上に存在する．

$AH$と$BC$の交点，$BH$と$CA$の交点，$CH$と$AB$の交点
線分$AH,BH,CH$の中点
線分$AB,BC,CA$の中点
　その円を九点円（フォイエルバッハ円）と呼ぶ．円の中心は$OH$の中点である．

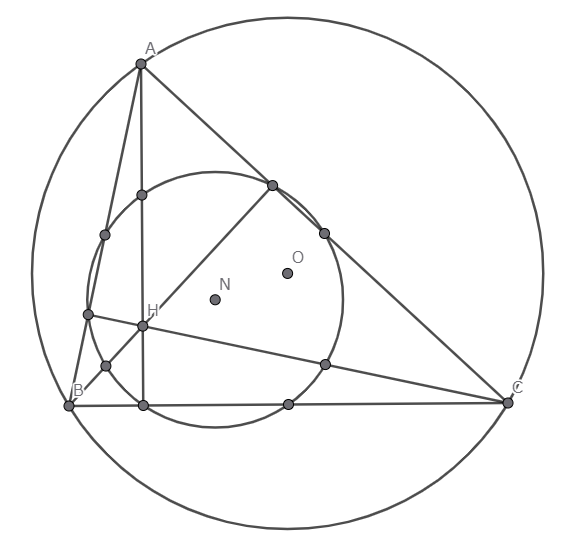
　九点円の存在の証明は，中点連結定理を使うのは最も単純だろう．参考として Wikipedia ．

　ベクトルが得意であれば（Euler線を含めて）以下の説明も好まれるだろう.
　$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$とおくと，$\overrightarrow{OH}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$が成り立つことが知られている．
　さらに重心の性質から$\overrightarrow{OG}=\dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}$なので，Euler線の性質が従う．
　次に$9$点円である．$BC$の中点，$AH$の中点をそれぞれ$M_1,M_2$とおくと，
　　$\overrightarrow{OM_1}=\dfrac{\overrightarrow{b}+\overrightarrow{c}}{2}, \overrightarrow{OM_2}=\overrightarrow{a}+\dfrac{\overrightarrow{b}+\overrightarrow{c}}{2}$
であり，その中点は$\overrightarrow{ON}=\dfrac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{2}$となる．これは線分$OH$の中点に一致する．
　また，$AH$と$BC$の交点を$D$と置くと，$\angle M_1DM_2=90°$より，点$D$は$M_1M_2$を直径とする円上に存在する．