文献あり

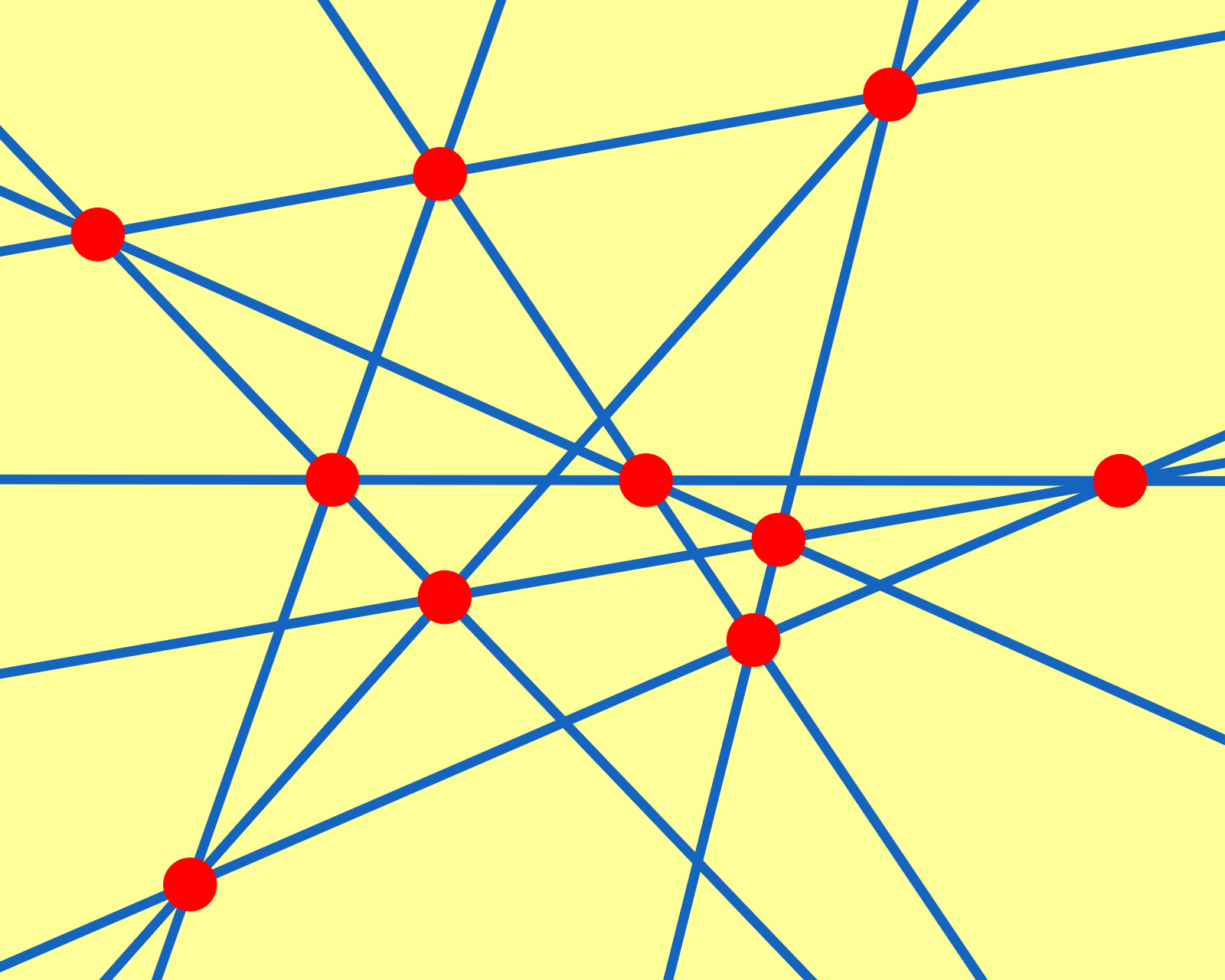
円に関する定理

メモ書きですが、公開にしておきます。

この定理や関連する定理の名称等があれば教えてください。
→ ミケルの定理により容易に証明可能でした。自己解決。(2026/1/5追記)
→ 定理1はミケルの六円定理でした。自己解決その2。(2026/1/9追記)

平面上に円または直線$\Gamma$があり、$\Gamma$上にある点$A,B$と$\Gamma$上にない点$C,D$を定める。
$\Gamma$上に点$X$をとり、円$ACX$と円$BDX$が再び交わる点を$Y$とする。
$X$が$\Gamma$上を動くとき、$Y$は$X$に依らない円または直線$\Omega$上にあり、$\Omega$は$C,D$を通る。
定理1 定理1

(2026/1/9 証明追加)

$\Gamma$上に点$X'$をとり、円$ACX'$と円$BDX'$が再び交わる点を$Y'$とする。
4つの円$ACX,BDX,ACX',BDX'$に対してミケルの六円定理を使うと、$A,B,X,X'$が共円なので$C,D,Y,Y'$も共円であることがわかる。
$X'$を固定して$X$を動かせば$Y$は固定された円$CDY'$上にあることになり、定理1が示された。

平面上に直線$\Gamma$があり、$\Gamma$上にある点$A$と$\Gamma$上にない点$C,D$を定める。
$\Gamma$上に点$X$をとり、円$ACX$と直線$DX$が再び交わる点を$Y$とする。
$X$が$\Gamma$上を動くとき、$Y$は$X$に依らない円または直線$\Omega$上にあり、$\Omega$は$C,D$を通る。
系1

系1は定理1における$\Gamma$を直線にして$B$を無限遠点にしたものとみなすことができます。

(2026/1/5 証明差し替え)

定理1において点$B$を中心とする反転を行うと系1に帰着されるので、系1のみ示せばよい。

以下、系1を証明する。

$\Gamma$上に点$X'$をとり、円$ACX'$と直線$DX'$が再び交わる点を$Y'$とする。
$\triangle DXX'$に着目して直線$DX,DX',XX'$上の点$Y,Y',A$についてミケルの定理を適用すると、$C,D,Y,Y'$が共円であることがわかる。
$X'$を固定して$X$を動かせば$Y$は固定された円$CDY'$上にあることになり、系1が示された。

差し替え前のバージョンも一応残しておきます。↓

(2026/1/1 最初に載せた証明)

定理1において点$B$を中心とする反転を行うと系1に帰着されるので、系1のみ示せばよい。

以下、系1を証明する。

この証明では、「円」という用語で「円または直線」を表す。

虚円点を$I,J$とする。
$\Gamma$上に点$X'$をとり、円$ACX'$と直線$DX'$が再び交わる点を$Y'$とする。
円$ACX$と直線$DX'$を合わせた三次曲線を$\tau_1$とし、円$ACX'$と直線$DX$を合わせた三次曲線を$\tau_2$とする。
$\tau_1,\tau_2$の交点は$A,C,D,X,Y,X',Y',I,J$である。
今、$A,X,X'$は一直線上にあるので、ベズーの定理の応用(dgの命題4)あるいはケイリー＝バッハラッハの定理の応用(cb)より、$C,D,Y,Y',I,J$は一つの円錐曲線上にある。すなわち$C,D,Y,Y'$は共円である。
$X'$を固定して$X$を動かせば$Y$は固定された円$CDY'$上にあることになり、系1が示された。