　問題は[こちら](https://www.imojp.org/archive/mo2024/selection_camp/problems/2024.pdf)から．

　元の問題は次の問題に言い換えられます．

&&&exc 問題*
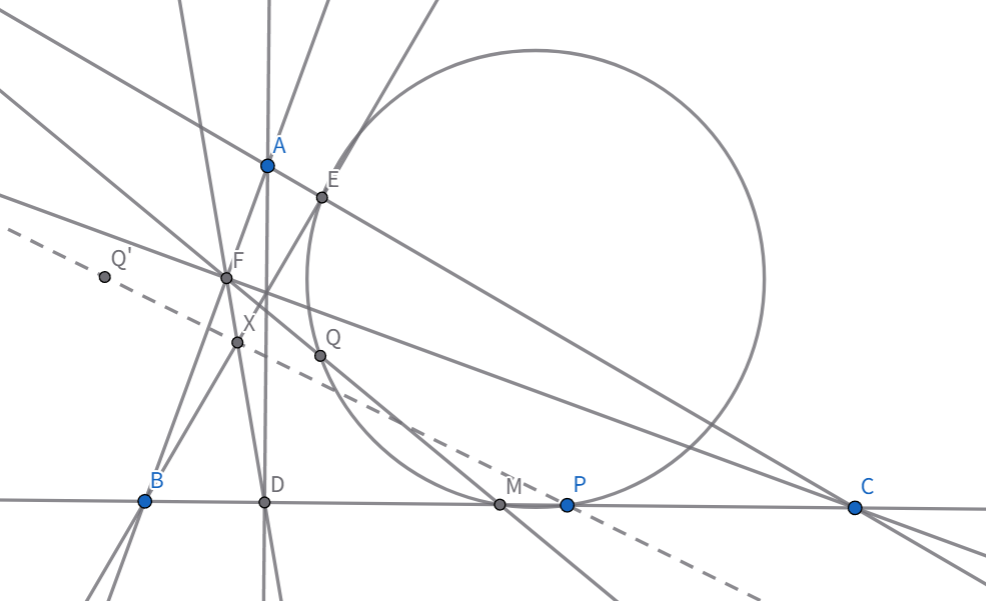
三角形$ABC$において，辺$BC$の中点を$M$とし，$A,B,C$から対辺に下ろした垂線の足をそれぞれ$D,E,F$とする．半直線$MC$上に点$P(\neq M)$をとり，円$MPE$と直線$MF$の交点を$Q(\neq M)$とする．$Q$を直線$AB$に関し対称移動した点を$Q'$とし，$DF$と$BE$の交点を$X$とすれば，$Q',X,P$は共線．![](/uploads/mathdown/qNff33D4YCW1x10sMIBU.png =500)
&&&

　これは，$FQ':DP=FQ:DP=EF:ED=FX:XD\quad(\because \triangle EFD\sim \triangle EQP)$と，$Q'F\parallel DP$から従います．$\blacksquare$




春24P12の不親切な解説

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント