【初投稿】三角比の範囲で2倍角・半角の公式を導く
はじめに
こんにちは、みのと申します。
Mathlogを書いてみたかったので、やってみます！
初めて…といいたいところですが、すでに同じ内容の記事を1回書いていてそれを消してしまったためもう1回書いています。悲しい
僕は、現在高1で数検準1級を取っています。大学数学もぼちぼち。今の目標は留数定理とやらで気持ちよくなることと、関数グラフアートに触れたりしたいなーと思っています。
三角比の範囲で2倍角・半角の公式
さて、最近思いついたことについてここに書いておこうと思います。高1の知識で三角関数の2倍角・半角の公式を導いてみようというものです。すでに誰かが書いていそうですが、一応自分が思いついたということで…
今回cosの場合を導きます。とりあえず下に示す形を導けば、変形して他のcos^2-sin^2みたいな形も出てきますね。
$\cos2 \theta=1-2sin^{2} \theta$
※三角形を使う関係上、$0°\lt \theta \lt90°$に限られます。まあ三角比の範囲ですし、そうでないとだめではありますね。
以下のようなAB=ACの二等辺三角形ABCを考える。
AB=AC=a,BC=b,$\angle$BAC=$2\theta$とする。
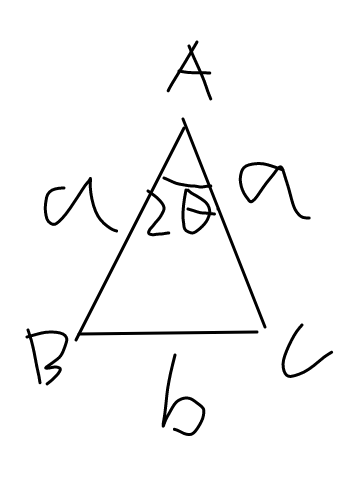手書きで汚いのは許して
また、$\angle$BACの二等分線とBCとの交点をDとすると、$\angle$BAD=$\angle$CAD=$\theta$,BD=DC=$\frac{b}{2}$,$\angle$ADB=$\angle$ADC=90°となる。
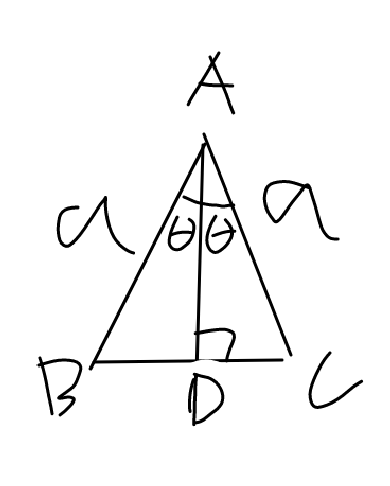手書きで（以下略）
三角形ABCにおいて、余弦定理より
$$
b^{2}=2 a^{2}-2 a^{2} \cos2\theta
$$
$b^{2}=2 a^{2} \left( 1-cos2\theta \right)$
また、
$$
\frac{b}{2}=BD=a \sin \theta
$$
$$
b=2a \sin \theta
$$
$$
b^{2}=4 a^{2} \sin^{2} \theta
$$
よって、
$$
2 a^{2} \left( 1-\cos2\theta \right)=4 a^{2} \sin^{2} \theta
$$
$$
a^{2} \neq0
$$より、
$$
1- \cos2\theta=2 \sin^{2} \theta
$$
あとは変形すれば目標の式を得られる
（最後の式は半角の公式のほうが分かりやすそう〜）
さいごに
加法定理でいいんじゃないんですかね
図形的なアプローチも楽しいですね。
これからも気づいたことを書き留めたり、勉強したことを書いてったりするかもしれないので見てくれると嬉しいです。
では！
この記事を高評価した人
この記事に送られたバッジ
投稿者
