中学数学でπ>3.14を示す。+sin3°を幾何学的に示す。

目次

０. はじめに
１. 流れ
２. 正五角形と黄金比
３. 半径1の円に内接する正五角形の1辺の長さを求める。
４. 18°,72°,90°の直角三角形の比を求める。
５. 15°,75°,90°の直角三角形の比を求める。
６. 3°,87°,90°の直角三角形の比を求める。
７. 半径1の円に内接する正120角形の面積を求める。
$ \quad(\mathrm{sin3°}$を幾何学的に示す。)
８. $\pi>3.14$
９. おわりに

０. はじめに

初めまして、$\mathrm{liber}$です。
今回は、円に内接する正120角形の面積から、
初等幾何で$\pi>3.14$を示していきたいと思います!

１. 流れ

「正120角形の１つの中心角が3°であることから、
　3°,87°,90°の直角三角形の辺の比を求めたい。」

→ 「18°-15°=3°より、
　　18°,72°,90°の直角三角形の辺の比と、　　
　　15°,75°,90°の直角三角形の辺の比を求めたい。」

→　$18°\times2$=36°より、
　　 36°,54°,90°の直角三角形の辺の比を求めたい。

２. 正五角形と黄金比

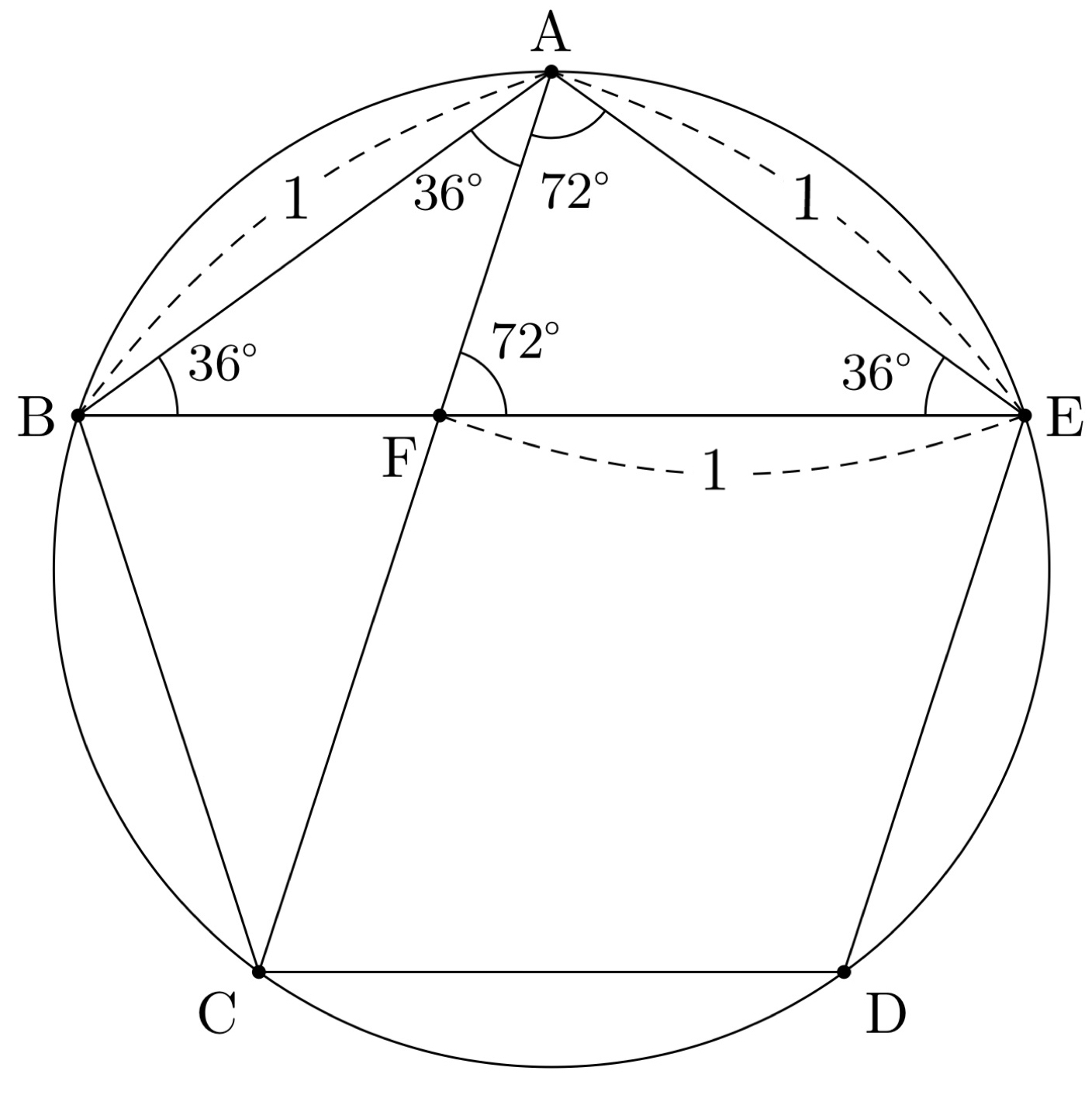正五角形①
$AB=1$とする。
$\triangle{ABF}\sim\triangle{BEA}$より、
\begin{eqnarray} AB:BE &=& BF:EA\\ 1:BF+1 &=& BF:1\\ BF(BF+1) &=& 1\\ BF^2+BF-1 &=& 0\\ BF>0より、BF &＝& \frac{-1+\sqrt5}{2} \end{eqnarray}
よって、$BE=BF+1=\frac{-1+\sqrt5}{2}+1=\frac{1+\sqrt5}{2}$

３. 半径１の円に内接する正五角形の1辺の長さを求める。

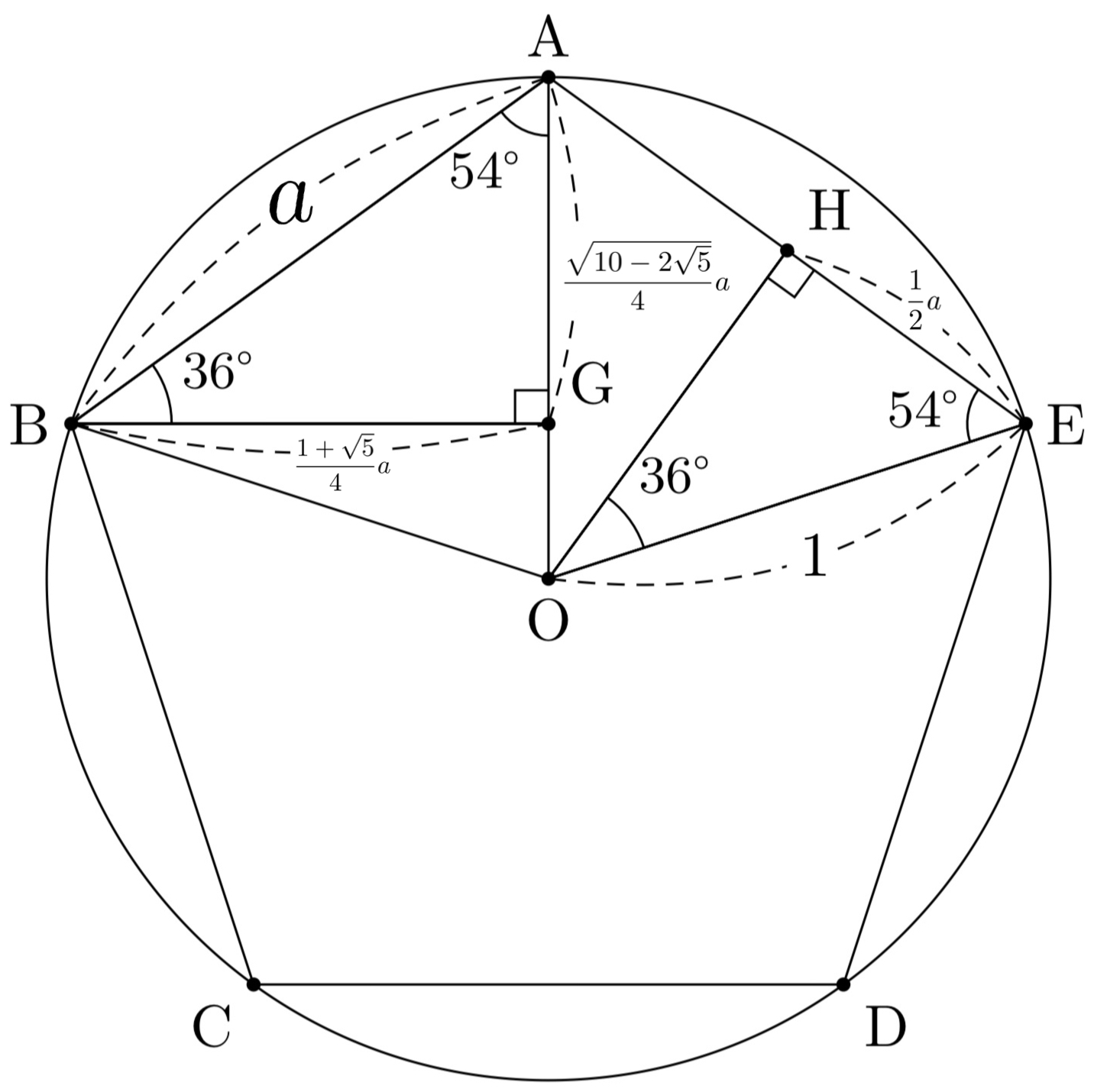正五角形②
$AB＝a$とおく。
前述から、$AB：BG＝1:\frac{1+\sqrt5}{4}$より、$BG=\frac{1+\sqrt5}{4}a$

ここで、$\triangle{ABG}$において、三平方の定理により、
$AG=\frac{\sqrt{10-2\sqrt5}}{4}a$を得る。

$\triangle{ABG}\sim\triangle{EOH}$より、
\begin{eqnarray} AB:EO &=& AG:EH\\ \hspace{1cm}\mathit{a}:1 &=& \frac{\sqrt{10-2\sqrt5}}{4}a:\frac{1}{2}a \end{eqnarray}
$$\therefore{a=\frac{\sqrt{10-2\sqrt5}}{2}}$$

よって、

４. 18°,72°,90°の直角三角形の比を求める。

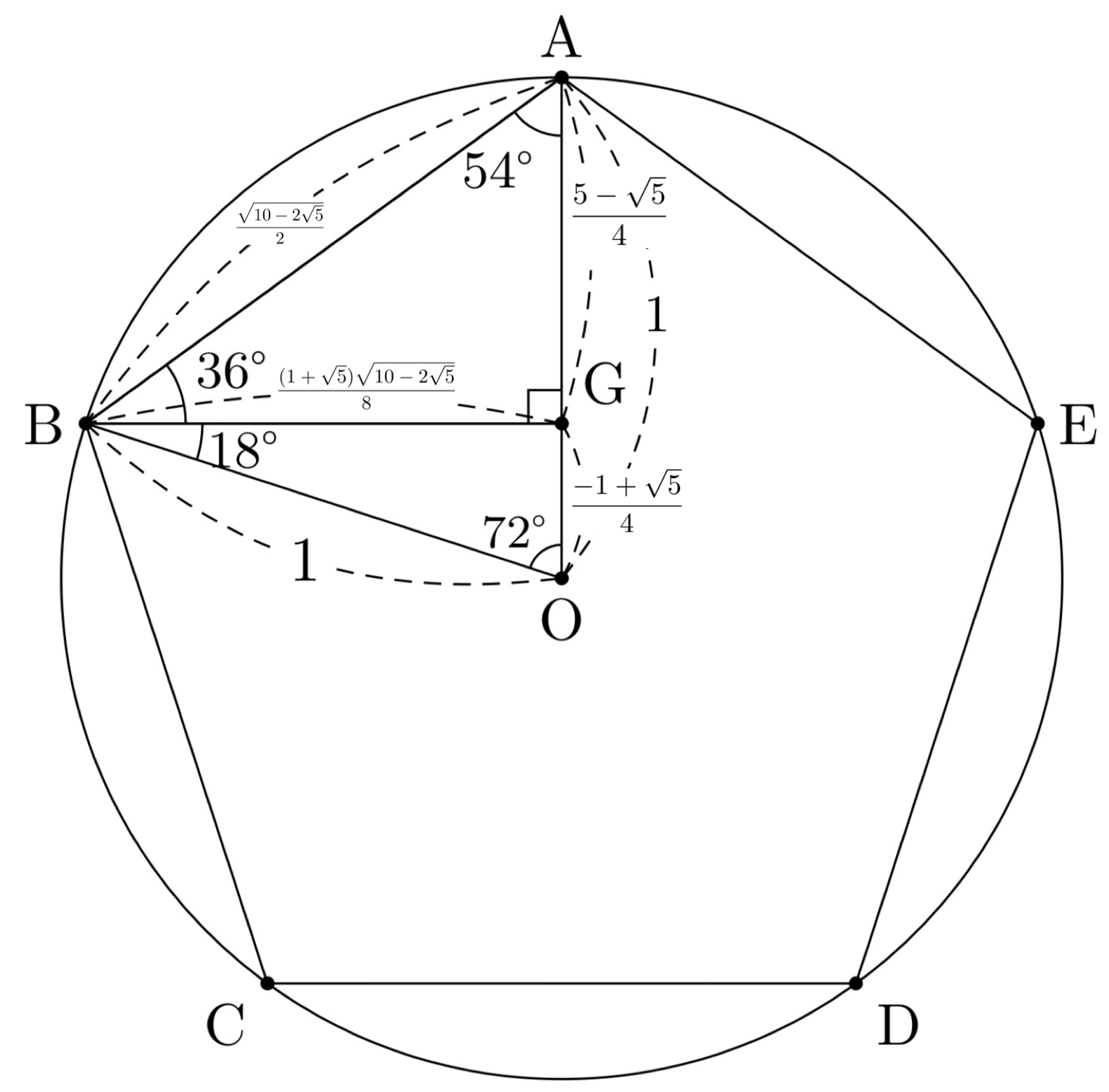正五角形③
前述から、$AB:BG:AG＝1:\frac{1+\sqrt5}{4}:\frac{\sqrt{10-2\sqrt5}}{4}$である。

よって、$AB=\frac{\sqrt{10-2\sqrt5}}{2}$のとき、

$BG=\frac{1+\sqrt5}{4}\times{\frac{\sqrt{10-2\sqrt5}}{2}}=\frac{(1+\sqrt5)\sqrt{10-2\sqrt5}}{8}\;,$

$AG=\frac{\sqrt{10-2\sqrt5}}{4}\times{\frac{\sqrt{10-2\sqrt5}}{2}}=\frac{5-\sqrt5}{4}\;,$

$GO=AO-AG=1-(\frac{5-\sqrt5}{4})=\frac{-1+\sqrt5}{4}$

よって、

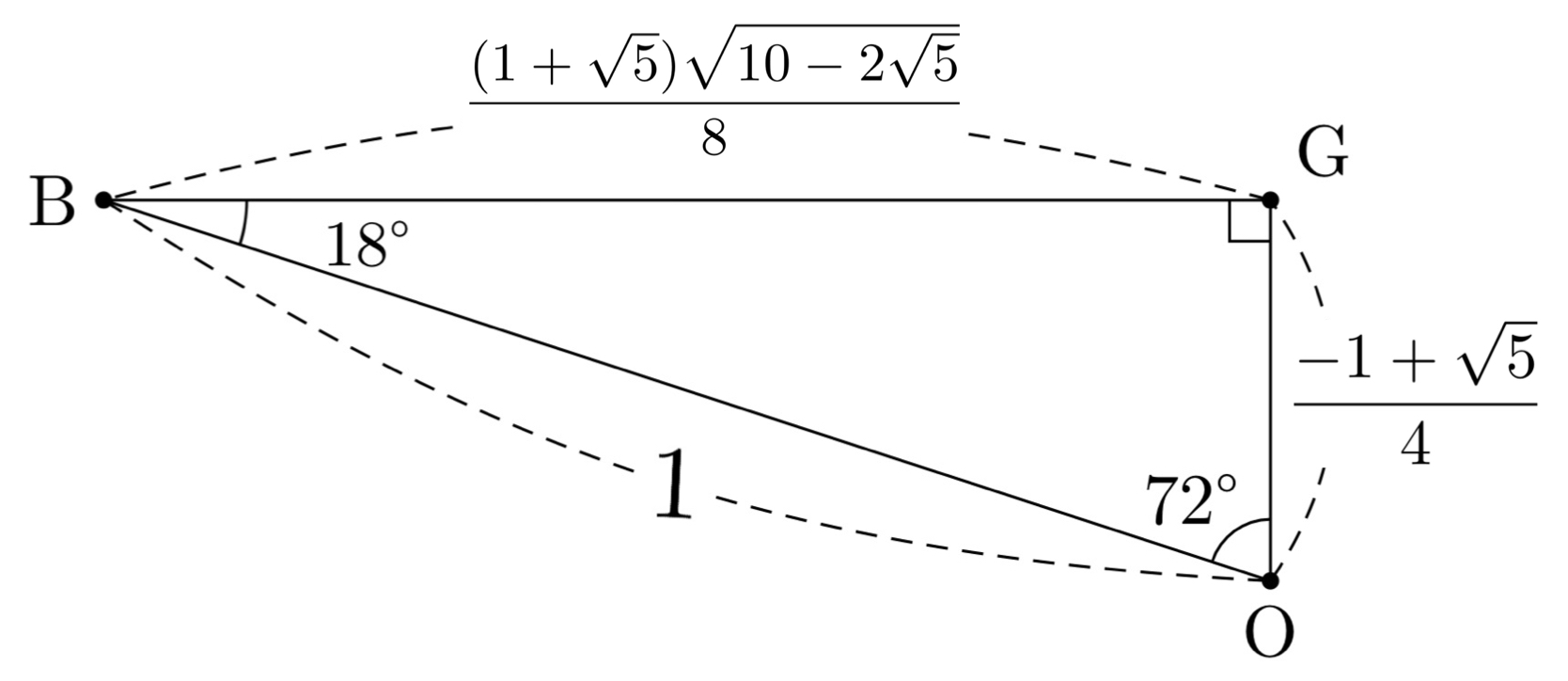18°,72°,90°の直角三角形①

５. 15°,75°,90°の直角三角形の比を求める。

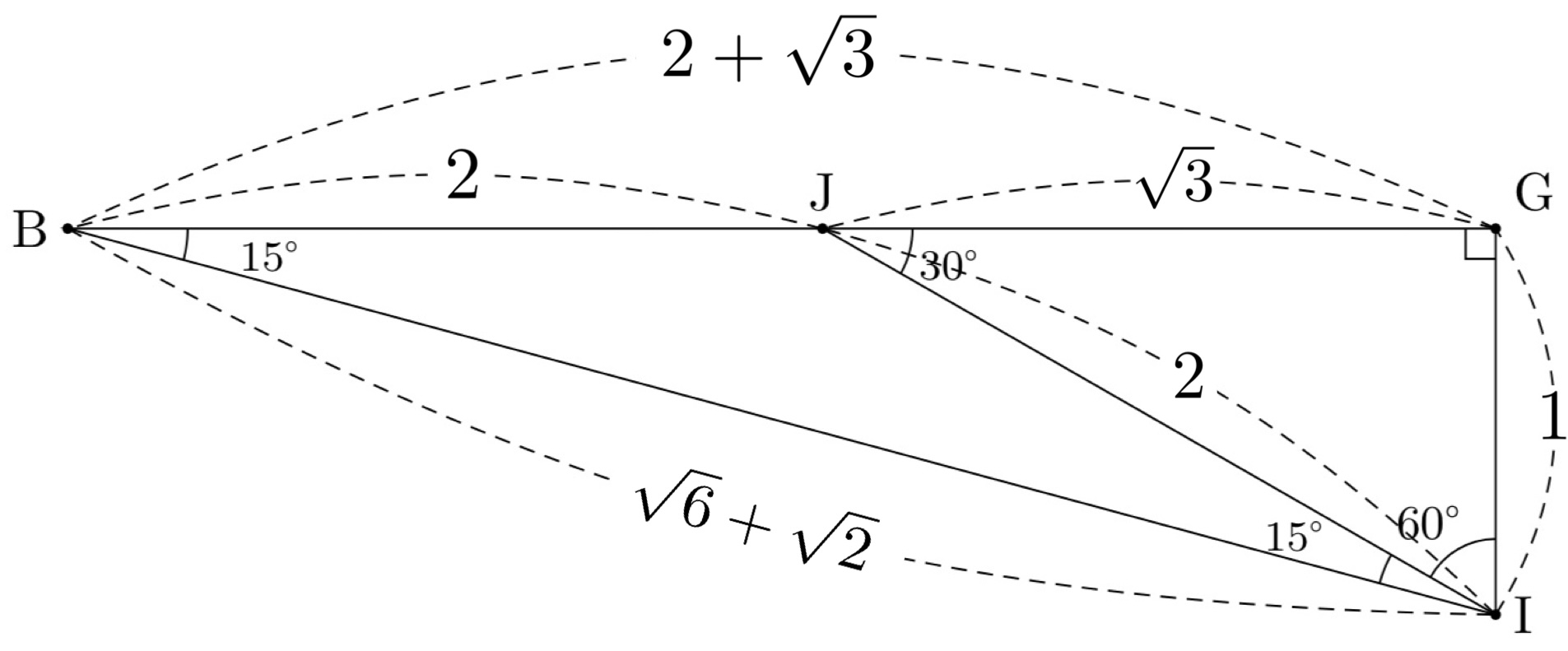15°,75°,90°の直角三角形
$GI=1$とすると、
$JI=JB=2,\quad JG=\sqrt3,\quad BG=2+\sqrt3$

$\triangle{BGI}$において、三平方の定理により、
$BI=\sqrt{8+4\sqrt3}=\sqrt{8+2\sqrt{12}}=\sqrt{(\sqrt6+\sqrt2)^2}=\sqrt6+\sqrt2$

よって、

６. 3°,87°,90°の直角三角形の比を求める。

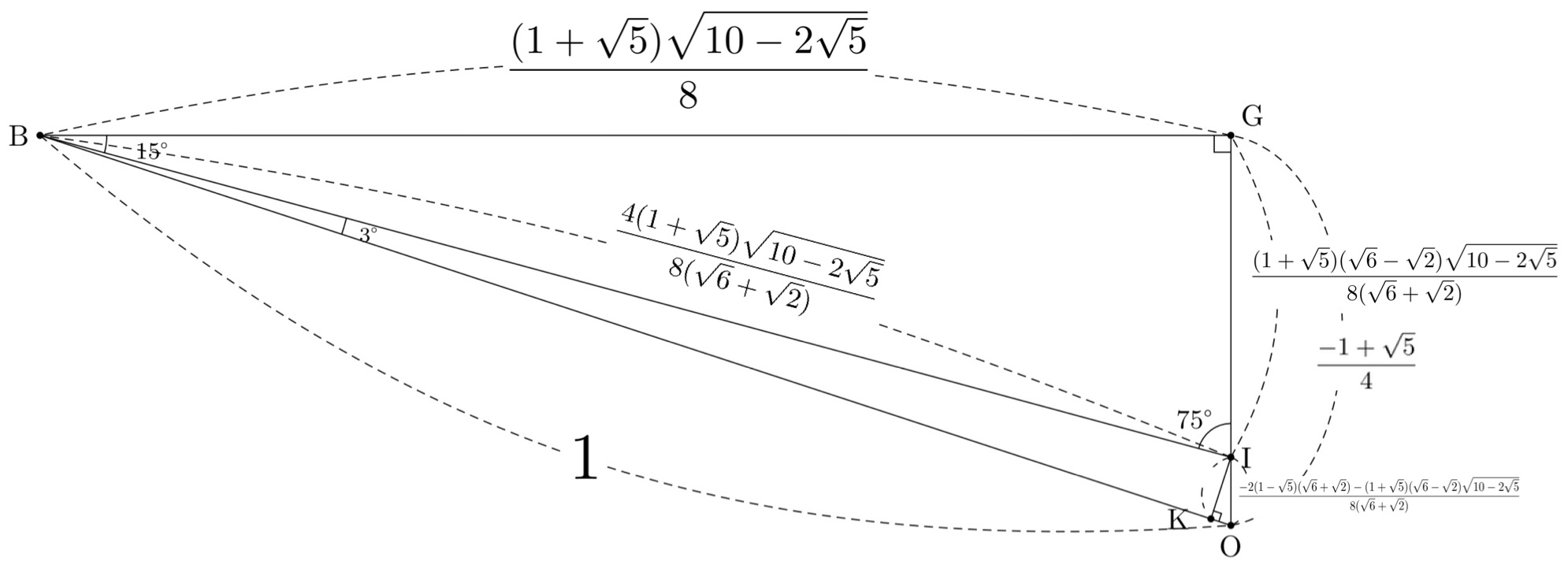18°,72°,90°の直角三角形②

前述から、$GI:BG:BI=\sqrt6-\sqrt2\;:\sqrt6+\sqrt2\;:4$である。

よって、$BG＝\frac{(1+\sqrt5)\sqrt{10-2\sqrt5}}{8}$のとき、

$BI=\frac{4(1+\sqrt5)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}\;,$

$GI＝\frac{(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}\;,$

\begin{eqnarray} OI &=& GO-GI\\ &=& \frac{-1+\sqrt5}{4}-\frac{(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}\\ &=& \frac{-2(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)} \end{eqnarray}

$\triangle{OBG}\sim\triangle{OIK}より、$
$OI:IK=OB:BG=1:\frac{(1+\sqrt5)\sqrt{10-2\sqrt5}}{8}$であるから、

$IK＝\frac{-2(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}\times\frac{(1+\sqrt5)\sqrt{10-2\sqrt5}}{8}$

よって、

７. 半径1の円に内接する正120角形の面積を求める。

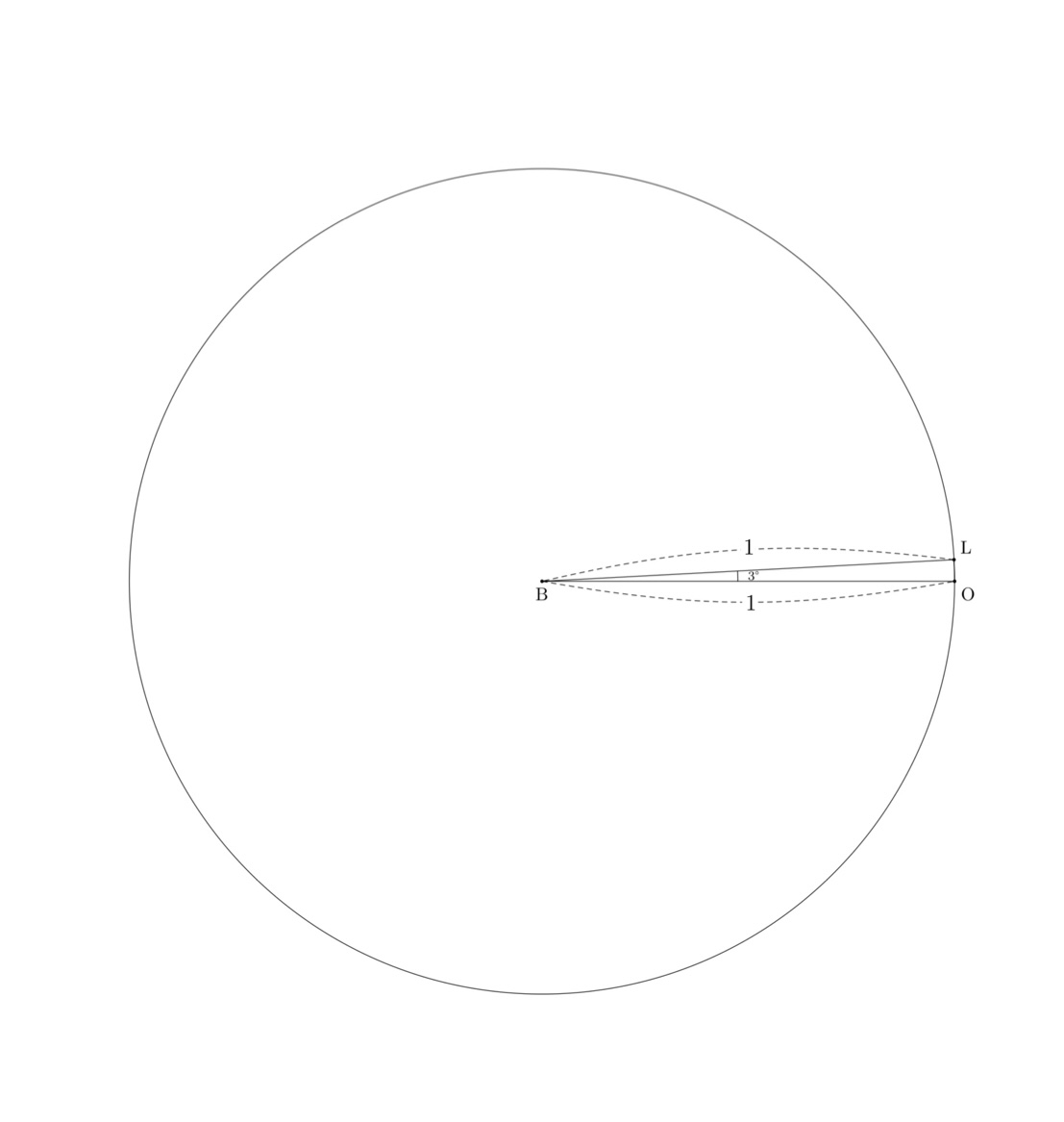正120角形の一部分
点$L$から辺$BO$に垂線を下ろした足を$M$とすると、
前述から、
$BL:LM$
$=\frac{4(1+\sqrt5)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}:\frac{-2(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}\times\frac{(1+\sqrt5)\sqrt{10-2\sqrt5}}{8}$である。

$BL＝1$のとき、
\begin{eqnarray} LM &＝& \frac{-2(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{8(\sqrt6+\sqrt2)}\times\frac{(1+\sqrt5)\sqrt{10-2\sqrt5}}{8}\times\frac{8(\sqrt6+\sqrt2)}{4(1+\sqrt5)\sqrt{10-2\sqrt5}}\\ &=& \frac{-2(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt6-\sqrt2)\sqrt{10-2\sqrt5}}{32}\\ &=& \frac{2\{-(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt3-1)\sqrt{5-\sqrt5}\}}{32}\\ &=& \frac{-(1-\sqrt5)(\sqrt6+\sqrt2)-(1+\sqrt5)(\sqrt3-1)\sqrt{5-\sqrt5}}{16}\\ &=& \frac{-(1-\sqrt5)(\sqrt6+\sqrt2)-2\sqrt{5+\sqrt5}(\sqrt3-1)}{16}\\ &=& \frac{\sqrt{30}+\sqrt{10}-\sqrt6-\sqrt2-2\sqrt{15+3\sqrt5}+2\sqrt{5+\sqrt5}}{16}\\ \end{eqnarray}

よって、

$\mathrm{sin3°}$はいくつ?
$\mathrm{sin}\theta,\mathrm{cos}\theta$
$\angle{C}=90°$の直角三角形ABCにおいて、$\angle{ABC}=\theta$とし、$$\mathrm{sin\theta}=\frac{AC}{AB},\quad \mathrm{cos\theta}=\frac{BC}{AB},\quad \mathrm{tan\theta}=\frac{AC}{BC}$$と定義する。

図6において、$$\mathrm{sin3°}=\frac{LM}{BL}=LM=\frac{\sqrt{30}+\sqrt{10}-\sqrt6-\sqrt2-2\sqrt{15+3\sqrt5}+2\sqrt{5+\sqrt5}}{16}$$
である。

８. $\pi>3.14$

円の面積は、半径$\times$半径$\times\pi$で求めることができる。
半径1のとき、円の面積＝$\pi$であるから、
半径1の円に内接する正120角形の面積$\approx$3.14015737より、$\pi>3.14$といえる。

９. おわりに

思い入れのある円周率を初記事として書けてよかったです。