微分　問題③

$x>0において、関数f(x)=\frac{\log x}{x}を考える$
$(1)x>1の時2\sqrt{x}>\log xを証明し、$$\underset{x\to \mathrm{\infty }}{lim}\frac{\log x}{x}の値を求めよ$$$
$(2)1,\sqrt{2},\sqrt[3]{3},\sqrt[4]{4},\sqrt[5]{5}の大小を判定しなさい$
$(3)e^{\pi },{\pi }^eの大小を判定せよ$

解説
(1)
$g(x)=2\sqrt{x}-\log xとする$
$$g^{\prime }(x)=\frac{1}{\sqrt{x}}-\frac{1}{x}=\frac{\sqrt{x}-1}{x}$$
$x>1の時g^{\prime }(x)>0であるからg(x)は単調増加$
$g(1)=2であるからx>1のときg(x)>2$
以上より、証明完了
$x>1の時、\log x>0であり、2\sqrt{x}>\log xであるから$
$0<\log x<2\sqrt{x}$
$$0<\frac{\log x}{x}<\frac{2}{\sqrt{x}}$$
$$\underset{x\to \mathrm{\infty }}{lim}\frac{2}{\sqrt{x}}=0であるから、はさみうちの定理より$$
$$\underset{x\to \mathrm{\infty }}{lim}\frac{\log x}{x}=0$$

(2),(3)
$f(x)のグラフを描く$
$$f^{\prime }(x)=\frac{x・\frac{1}{x}-\log x}{x^2}=\frac{1-\log x}{x^2}$$
$f^{\prime }(x)=0を解くと、x=e$
増減表を書くと、

$$\underset{x\to \mathrm{\infty }}{lim}f(x)=0であるから、$$
グラフを書くと、

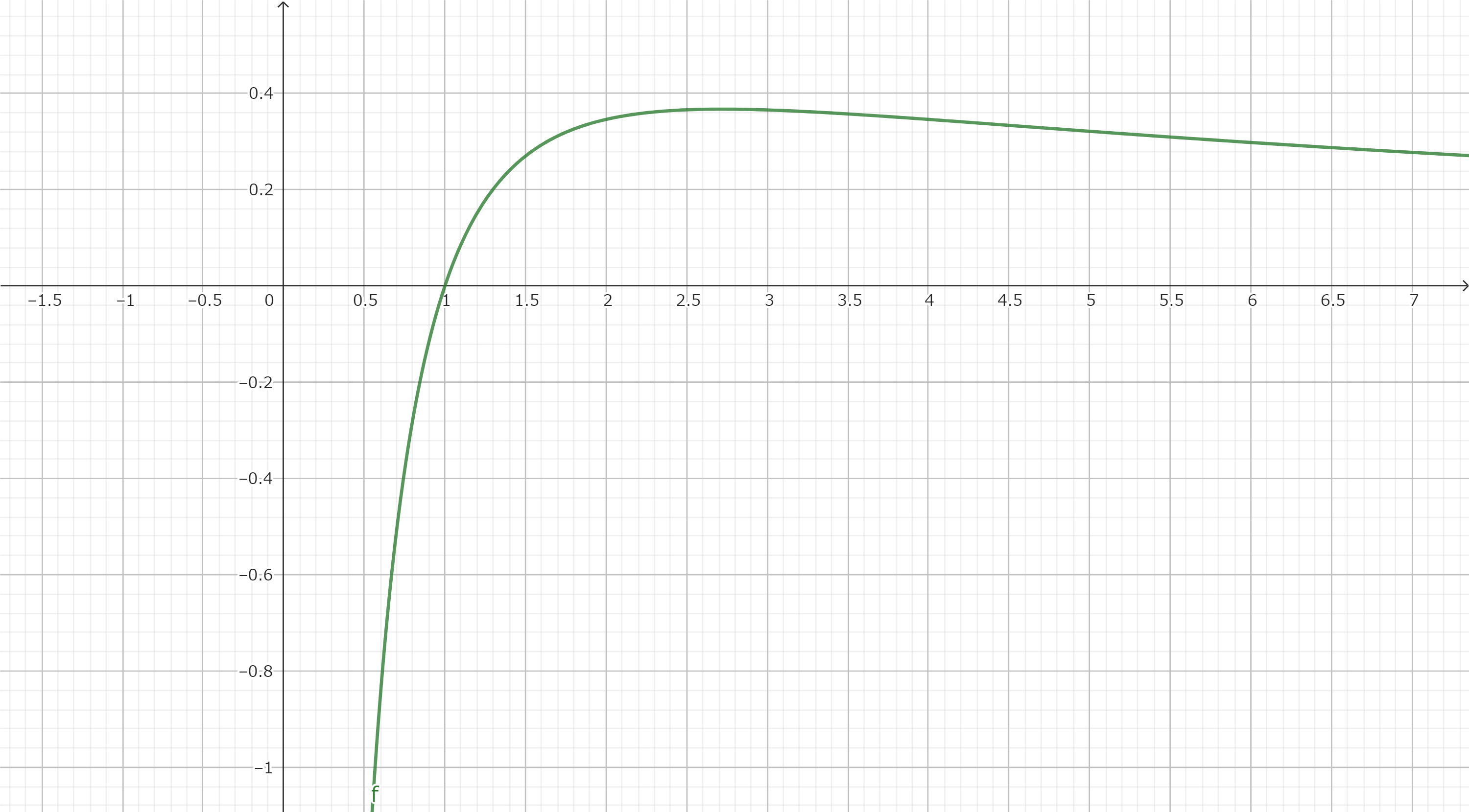
となる

(2)
すべて正の実数であるから、eを底として対数を取っても大小関係は変化しない。つまり
$$\frac{\log 1}{1},\frac{\log 2}{2},\frac{\log 3}{3},\frac{\log 4}{4},\frac{\log 5}{5}$$の大小を比較すれば良い
図1にプロットすると、

となる
$$\frac{\log 3}{3}-\frac{\log 2}{2}=\frac{2\log 3-3\log 2}{6}=\frac{\log \frac{9}{8}}{6}>0より、$$
$$\frac{\log 3}{3}>\frac{\log 2}{2}=\frac{\log 4}{4}>\frac{\log 5}{5}>\frac{\log 1}{1}$$であるから、
$\sqrt[3]{3}>\sqrt[2]{2}=\sqrt[4]{4}>\sqrt[5]{5}>1$である

(3)
両方正の実数であるから、eを底として対数を取っても大小関係は変化しない。よって
$\pi \log e,e\log \pi$と大小を比較すればよい
また、$e\pi$>0より、$e\pi$で割っても大小関係は変化しない。よって、
$$\frac{\log e}{e},\frac{\log \pi }{\pi }の大小を比較すればよい。$$
$f(x)はx=eで極大であるから、$
$$\frac{\log e}{e}>\frac{\log \pi }{\pi }$$である。
よって$e^{\pi }>{\pi }^e$