前田数学模試中学生

大問1(25点)
画像の名前
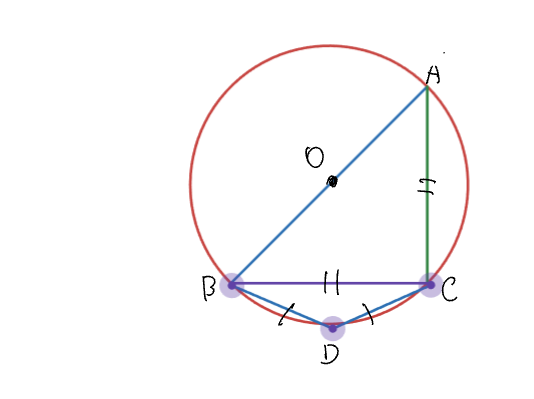
$A,B,C,D$は円周上にあり$O$は半径1の円の中心、線分$AB$は直径である。
(1)$\angle{BCD}$の角度を求めよ。
(2)$\triangle{BCD}$の面積を求めよ。
　　　　　　　　　　　　　　　　　　　　　　[2025年九州大学理系改]
(1)・・・7点
(2)・・・18点

大問2(25点)
画像の名前
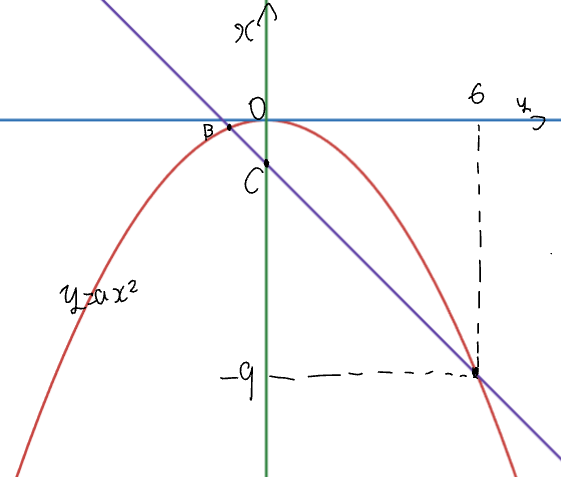
図のように、関数$y=ax^2(a<0)$のグラフ上に2点$A,B$をとり、点Aの座標を$A(6,-9)$、直線ABと$y$軸との交点を$C$とする.
また、$\triangle{OAB}$と$\triangle{OBC}$の面積比が$3:1$である。
(1)$a$の値を求めよ。
(2)直線ABの式を求めよ。
(3)$\triangle{OAB}$の面積を求めよ。
(4)点$C$を通り、$\triangle{OAB}$の面積を二等分する直線の式を求めよ。
(1)・・・3点
(2)・・・4点
(3)・・・7点
(4)・・・11点

大問3(25点)
図形A
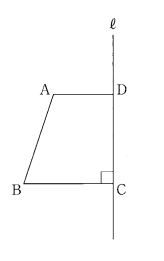
線分$AD=4$,線分$BC=6$とするとき、線分$CD=5$とする。(円周率=π)
(1)$l$を軸として、一回転させたときの体積を求めよ.
(2)(1)の立体の表面積を求めよ。
(3)$BC$を軸として、一回転させたときの体積を求めよ.
(4)(3)の立体の表面積を求めよ.
(1)・・・3点
(2)・・・3点
(3)・・・9点
(4)・・・10点

大問4(25点)
(1)$(\frac{\sqrt{3}+1}{2})^2-2(\frac{\sqrt{3}+1}{2})(\frac{\sqrt{3}-1}{2})+(\frac{\sqrt{3}-1}{2})^2$を簡単にせよ。
(2-a)$x^2-y^2+2x-2y$を因数分解せよ.
(2-b)$x^2-y^2+2x-2y-40=0$をみたす正の整数の組$(x,y)$をすべて求めよ.
(3)$\frac{\frac{3}{4}+\frac{1}{20}}{\frac{7}{12}+\frac{1}{1+\frac{1}{2}}}$を計算せよ.
(4)$1,2,3,4,5$の$5$つの数字を並びかえてできる$5$桁の整数を小さい順に並べたとき、$34251$は何番目の整数か答えよ.
(1)~(5)・・・各5点

大問5(25点)

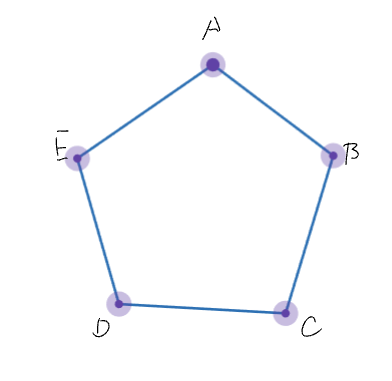
正五角形ABCDEの頂点を移動する点Pがある。点Pはさいころを投げて出た目の数だけ頂点を時計回りに移動する。点Pが、ちょうどAに止まったときは終了し、Aに止まらなかった時さらにさいころを投げ、その頂点から移動する。点Pが頂点Aからスタートするとき、次の問いに答えよ。
(1)さいころを2回投げて終了する目の出方は何通りあるか。
(2)ちょうど1周して終了する目の出方は何通りあるか。
(3)さいころを5回投げ、ちょうど2周して終了する目の出方は何通りあるか。
(1)・・・5点
(2)・・・7点
(3)・・・13点

満点・・・125点　回答時間・・・80分
偏差値(予想)
90〜125・・・偏差値70以上
70〜90・・・偏差値60以上
40〜70・・・偏差値50以上
0〜40・・・偏差値50以下