JMO2012本選4

334

JMO2012-4を割と公式解説と違う感じで解いた気がするので書きます．~~ほらそこ，遠回りしてるだけだなんて言わない~~

注意　位置関係は ~~面倒なので~~ 簡略化のため図のやつで考えています．

　平面上に三角形 $P A B$ と $P C D$ がある． $P A = P B, P C = P D$ であり， $P, A, C$ および $B, P, D$ はそれぞれこの順に同一直線上にある． $A, C$ を通る円 $S_{1}$ と $B, D$ を通る円 $S_{2}$ が異なる $2$ 点 $X, Y$ で交わっているとする．このとき，三角形 $P X Y$ の外心は $S_{1}$ の中心と $S_{2}$ の中心の中点であることを示せ．

図を書く

!FORMULA[14][1281108292][0]力が欲しい $GeoGebra$ 力が欲しい
　図を書きました． $S_{1}, S_{2}$ の中心を $O_{1}, O_{2}$ とし， $O_{1} O_{2}$ の中点を $O$ として， $O$ が $△ P X Y$ の外心であることを示します． $O_{1} O_{2}$ は $X Y$ の垂直二等分線なので何かしらのあと一つの条件が来たら勝ちです．

条件を睨む

　 $P A = P B, P C = P D$ が成り立っているらしいです．キモすぎるのでどうにかしたいです．...よく見たら $P A \times P C$ は左の円 $(S_{1})$ の方べきに， $P B \times P D$ は右の円 $(S_{2})$ の方べきになっています．いい感じに方べきの定理で回りそうです．

方べきの定理を回す

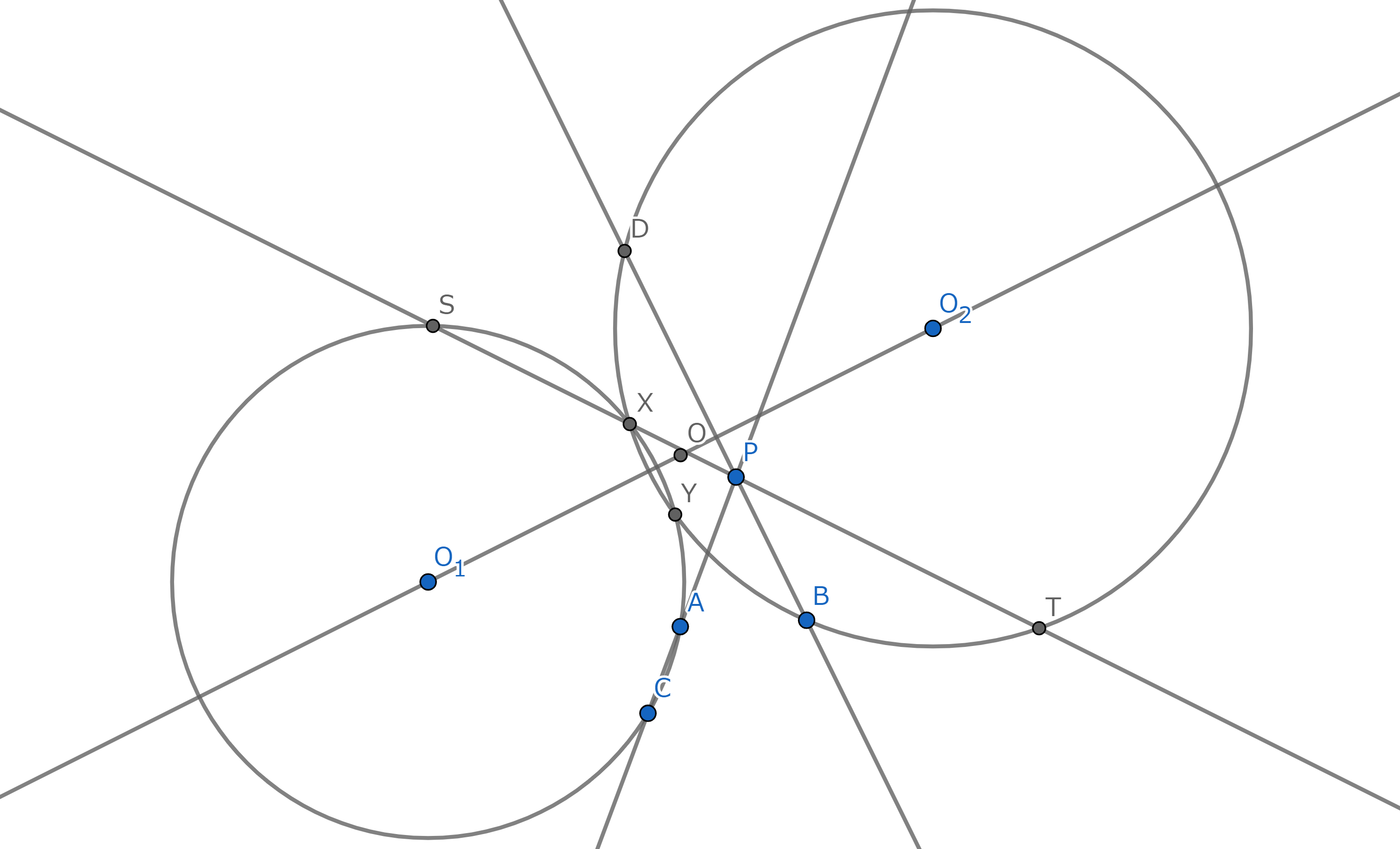GeoGeb力
　まず $X$ から回します． $P X$ と $S_{1}, S_{2}$ の交点を $S, T$ とすると，方べきの定理から次が成り立つことが分かります．
$P X \times P T = P B \times P D = P A \times P C = P X \times P S$
これから $P T = P S$ ，すなわち $P$ が $S T$ の中点であることが分かります．嬉しい．

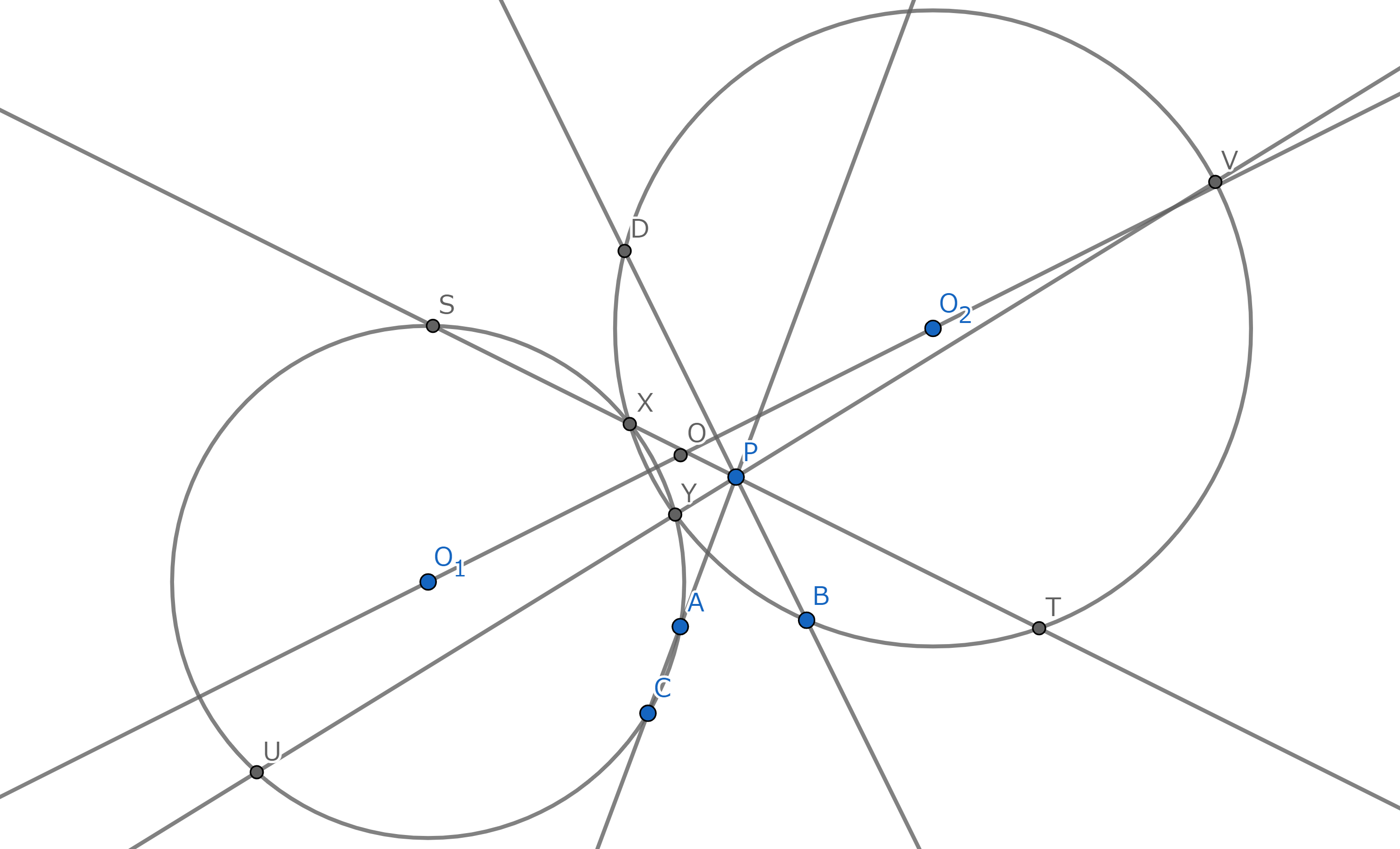G
　同様に $Y$ でも $U, V$ を作ってあげると $P$ は $U V$ の中点になります． $S U T V$ は平行四辺形ですね．

点を削除

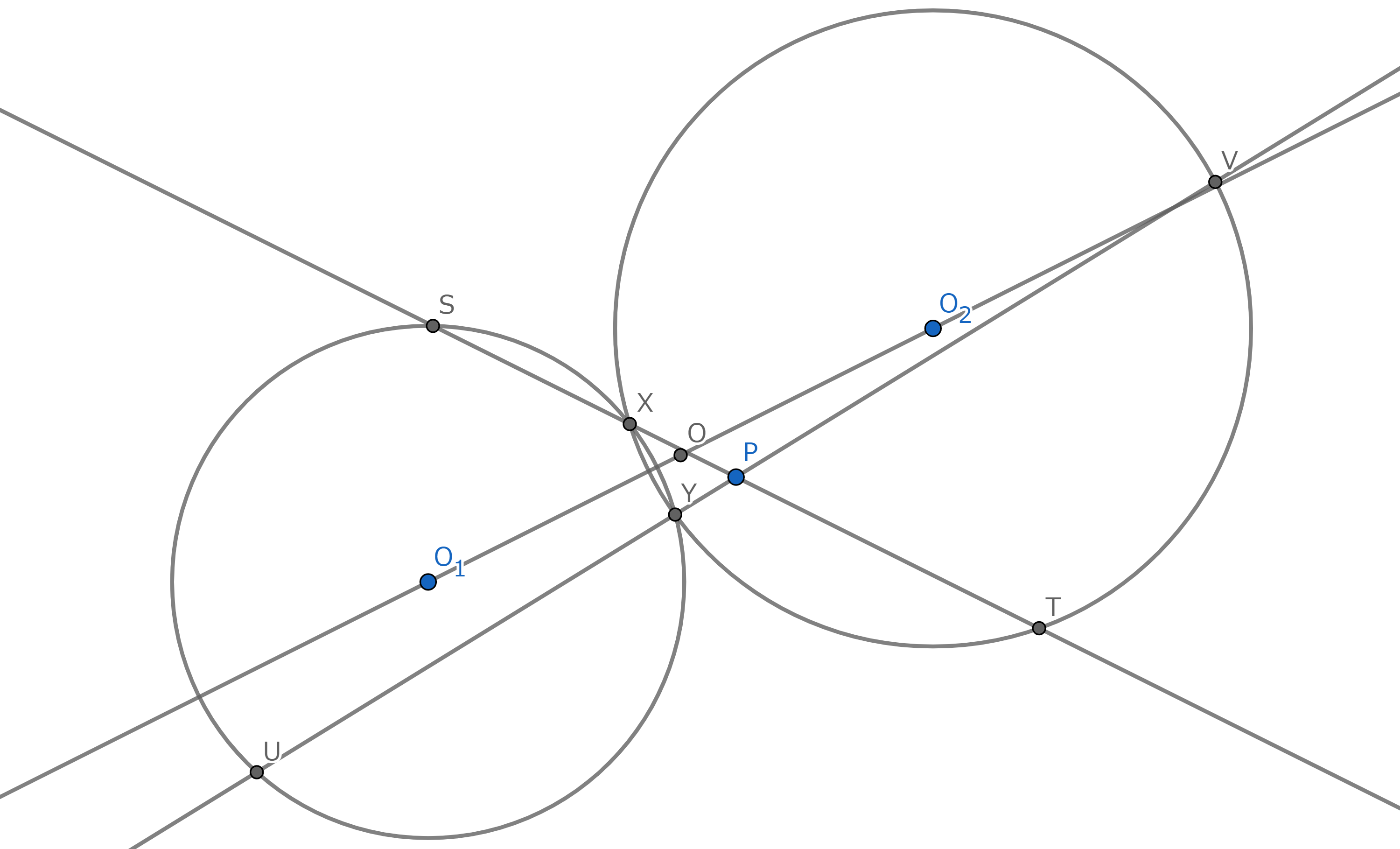いらない点と線が消えてくれました！
　平行四辺形の対角線上に $X, Y$ が乗ってていい感じに共円がある，みたいな感じに簡略化できました．あとは何しても解ける雰囲気があります．（aminoの補題だーって感じの図してますね）

計算！

　何してもよさそうなので $O$ が $X P$ の垂直二等分線上にあることを示します． $X Y$ の垂直二等分線上にあることは既に分かっているのでこれを示せれば終わりです．

　 !FORMULA[45][37081][0]と!FORMULA[46][1149640][0]が重なっていて極度に見づらい $O$ と $O^{'}$ が重なっていて極度に見づらい
　 $O, O_{1}, O_{2}$ から $X P$ に下ろした垂線の足を $O^{'}, O_{1}^{'}, O_{2}^{'}$ とします． $O_{1}^{'} O_{2}^{'} = O_{1}^{'} X + X O_{2}^{'} = \frac{S X}{2} + \frac{X T}{2} = \frac{S T}{2} = S P$ から $P O_{2}^{'} = S O_{1}^{'} = O_{1}^{'} X$ なので $O^{'}$ は $X P$ の中点だと分かります．したがって $O$ は $X P$ の垂直二等分線上にあることが分かりました．やったぜ．