コラッツ予想の証明についての考察！偶数を奇数になるまで2で割り続けたときの偶数と奇数の関係においてわかったこと

コラッツ予想の計算について、最近、振り返りをして気づいたことがあります。

最近、わたし、一般項、一般項って言い続けていますが、ほんとは一般項、というのは後付けだったのです。
一番最初にコラッツ予想を考察したときには、偶数だけを見ていました。
なので今みたいに「二重数列である一般項による証明」ではなくて2023年5月頃には「偶数の特性による証明」と呼んでいました。

一番最初の「わかったかも・・・」というのは、偶数を分解したときでした。
偶数の分解は、$a_{s,t}$=$2^s$×(2t-1)という式で表わせるわけですから、やっぱり一般項ではあるのですが・・・。
偶数を２で割り続けると奇数になることから、偶数を２の累乗と奇数の積で表すことにします。
連続する偶数でその分解をして並べてみると気づくことがあります。

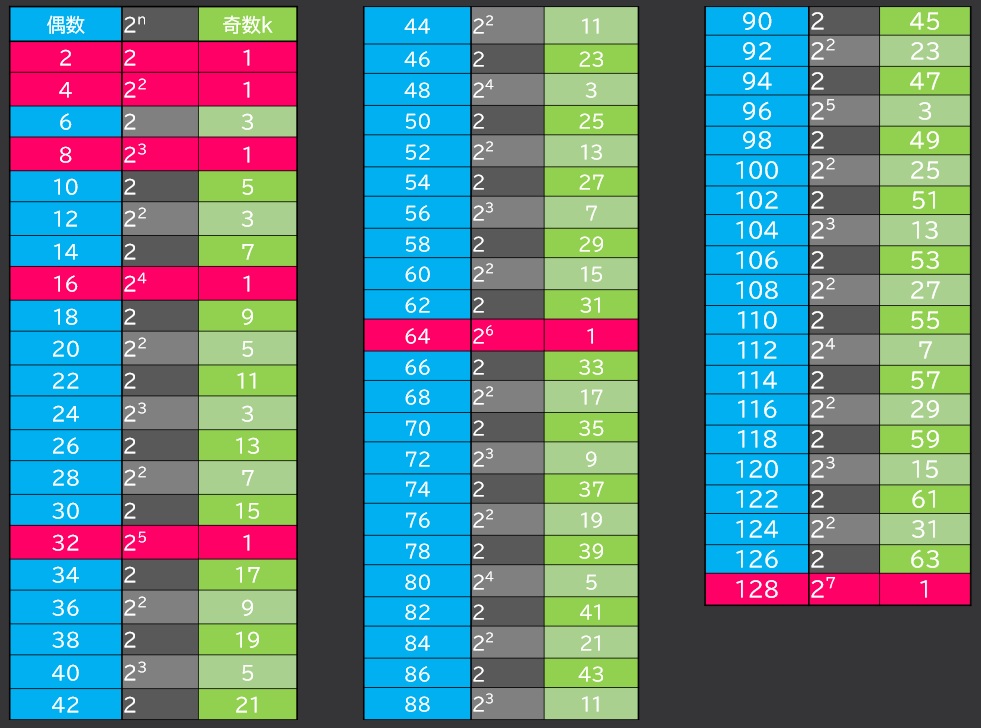
ピンクの行の偶数は、2の累乗である偶数です。この偶数 $2^s$と$2^{s+1}$の間の偶数の個数は、数が大きくなるにつれて、多くなっていきます。そして、その間の奇数は、一見ランダムに見えますが、3からの連続する奇数で、現れ方には規則性があります。
偶数 $2^s$と $2^{s+1}$の間の偶数の数列に、数が何個あるかを計算すると、偶数の
定義から、ｓ≧１において
($2^{s+1}$-$2^s$)/2-1 =$2^s$-$2^{s-1}$-1
=$2^s$×(1-$2^{-1}$)-1
=$2^s$×$2^{-1}$-1
=$2^{s-1}$-1
と偶数の個数は求められます。
偶数$2^s$と$2^{s+1}$の中央値の奇数は、いつも3です！
計算してみると・・・
s≧２のとき、偶数$2^s$と$2^{s+1}$の中央値をMとおくと、
M =($2^{s+1}$+$2^s$)/2
=($2^{s+1}$+$2^s$)×$2^{-1}$
=$2^s$+$2^{s-1}$
=$2^{s-1}$×(2+1)
=$2^{s-1}$×３
となるからですね。
S≧３のとき、偶数$2^s$とMの間にある偶数の、中央値をM´とおくと、
M´ =($2^s$+3×$2^{s-1}$)/2
=($2^s$+3×$2^{s-1}$)×2-1
=$2^{s-1}$+3×$2^{s-2}$
=$2^{s-2}$(2+3)
=$2^{s-2}$×5
S≧３のとき、偶数M´と$2^{s+1}$の間にある偶数の、中央値をM＂とおくと、
M＂=(3×$2^{s-1}$+$2^{s+1}$)/2
=(3×$2^{s-1}$+$2^{s+1}$)×$2^{-1}$
=3×$2^{s-1}$+$2^s$
=$2^{s-2}$(3+$2^2$)
=$2^{s-2}$×7
同じように、偶数$2^s$とM´、M´とＭ、ＭとM＂、M＂と$2^{s+1}$の中央値を計算すると、$2^{s-3}$×9、
$2^{s-3}$×11、$2^{s-3}$×13、$2^{s-3}$×15 となる。
それぞれ、また次の層で中央値を求めると、$2^{s-4}$×17、$2^{s-4}$×19、$2^{s-4}$×21、$2^{s-4}$×23、$2^{s-4}$×25、
$2^{s-4}$×27、$2^{s-4}$×29、$2^{s-4}$×31 となる。
このように、偶数の分解において得られる奇数が同じであるときの２の次数ｓは、2の累乗で囲まれた数列をひとつ大きくなる方向に進むと、１ずつ増えていきます。
これらのことより、コラッツの計算で得られる自然数を並べると、重複なくもれもなく、表わせそうだなと感じました。この表で発見したのです。
この表は、証明の原点です。
ただし、ループや発散が起こらないための奇数から偶数への接続については、別の説明が必要になってきます。ループや発散が起こらないためには、『3x+1』あるいは『x+1』で接続しなければなりません。
これらを説明するときには、一般項を用いることが一番わかりやすいと思い、手段として一般項を示すことを選びました。