素数に関するBonseの不等式を証明する
この記事を通して, 素数を小さい順に$p_1, p_2, ...$とします(例えば$p_1=2, p_3=5$.). また$n$以下の素数の総積を$n\#$とします.
$n$が$4$以上の整数であるとき, $p_n\#=p_1p_2\cdots p_n>p_{n+1}^2$
この素数に関する不等式を初等的に示してみたいですね. 別にBertrand-Chebychevの定理などを使えば早いんですが, 使わない縛りで示すことを目指しましょう.
任意の正の整数$n$に対し, $n< p\leq 2n$を満たすような素数$p$が存在する.
この定理から, $p_i\leq 2^i$という上限が得られますし, 隣接する素数同士がどれくらい離れているかを考えるときにも便利です(この記事では使えませんが). 別に初等的な証明あるし使っていいような気もするけど
Bonseの不等式をいきなり証明することは難しそうです. そのためまずは, Bonseの不等式に近い不等式を簡単に証明できないか考えてみましょう. $2$乗は怠いので, 一次にします. ただそれだけだと味気ないので, 次のようにしましょう:
任意の正数$c$に対し, ある$N$が存在し, $n>N$なる任意の正の整数$n$に対し, $p_n\#>cp_{n+1}$が成り立つ.
証明は$c=1$のときを考えて, それを一般に応用するつもりで簡単に思いつくと思います.
$p_k\#>c$なる最小の正の整数$k$を取る(このような$k$が存在することは素数の無限性から明らか). また$N=2k$とする. $P=p_k\#,\quad Q=\dfrac{p_n\#}{p_k\#}$とすると, $n>N=2k$に注意すれば$Q$は整数であり, $Q>P$が成り立つ.
さて, $Q-P$について, $p_n$以下の素数はすべて$Q, P$のどちらか一方のみを割り切るから$Q-P$を割り切ることはない. よって$Q-P$は$p_{n+1}$以上の素因数しかもたない. 明らかに$Q-P\neq 1$であるから, $Q-P\geq p_{n+1}$. よって
$$
QP\geq Pp_{n+1}+P^2>Pp_{n+1}>cp_{n+1}
$$
が成り立ち, これは目標の式である.
以上から命題は示された.
ちょっとは素数不等式への耐性が付いたので, Bonseの不等式のように$p_{n+1}^2$の形で評価できないかを考えたくなります. $c=p_{n+1}$ならいいんですが, 無理そうですね(やってみてください).
さっきの証明を思い出しましょう. やっていたのは
- $Q-P$という$p_{n+1}$以上の素数の「住処」を作る
- その住処をもとに$p_{n+1}$を上から評価する
ということです. しかし「住処」から直ちに導かれる不等式は一次なので, $p_{n+1}^2$の評価は困難です. 一つの「住処」では不可能, ということなので複数の「住処」を使います.
$4$以上の整数$k$に対し,
正整数$i$に対し, $m_i=i(p_{k-1}\#)-1$と定義し, $M=\{m_i \mid 1\leq i\leq p_k, i\in\mathbb{N}\}$とする. 明らかに$M$の任意の要素は$p_k$以上の素因数しかもたない.
$M$の要素$m_i, m_j$($1\leq i< j\leq p_k$)をともに割り切る素数$p$の存在を仮定しよう. すると$p\mid m_j-m_i$であるから
$$
p\mid (j-i)(p_{k-1}\#)\quad\therefore p\mid j-i
$$
であるが, これは不可能である. よって$M$の任意の要素はどの二つについても互いに素である.
$M$に$1$は含まれず, $|M|=p_k$であるから, $M$の要素のうち, $p_{k+p_k-1}$以上の素因数で割り切れる要素$m_x$が存在する. よって
$$
p_{k+p_k-1}\leq m_x\leq m_{p_k}=p_k\#-1
$$
であり, したがって$p_k\#>p_{k+p_k-1}$が成り立ち, $p_k\geq k+3$であるので$p_k\#>p_{2k+2}$である. 故に
$$
\begin{align*}
p_{2k}\#>&(p_k\#)^2>p_{2k+2}^2>p_{2k+1}^2\\
p_{2k+1}\#>&(p_k\#)^2>p_{2k+2}^2
\end{align*}
$$
となるので, $n\geq 8$についてBonseの不等式は示された($n=2k, 2k+1$についてBonseの不等式を確認したため). $n=4, 5, 6, 7$については手計算により成立が分かる.
これは"Another way to prove Bonse's inequality"(Bonseの不等式の別証明)という論文(?)で紹介されていた手法です(私が思いついたわけではない).
https://www.researchgate.net/publication/374023300_Another_way_to_prove_Bonse's_inequality
私もBonseの不等式の証明を試みましたができませんでした. この証明では複数の「住処」について議論することで$p_k\#>p_{k+p_k-1}$という強い事実を導いたのが大きかったですね.
これで終わるのも負けた気がするので, $c$を正定数として$p_n\#>p_{n+1}^c$を十分大きな$n$に対して示します. そのために次の補題を示しておきます:
任意の正数$c$に対し, ある$N$が存在し, $n>N$なる任意の正の整数$n$に対し, $p_n>cn$が成り立つ.
問題を言い換えると, $\pi(cn)< n$となります(ここで$\pi$は素数計数関数). $cn$までの正の整数を何らかの正整数$P$で分割することを考えましょう. $P$と$2$以上の公約数を持つ数は基本的に素数でないので, 一つの区間に含まれる素数は高々$\varphi(P)$個!と言いたくなりますが, $1$から$P$までの場合はそうはいきません. しかし, $n$を十分大きく取ることを考えるとそこまで問題はなさそうです:
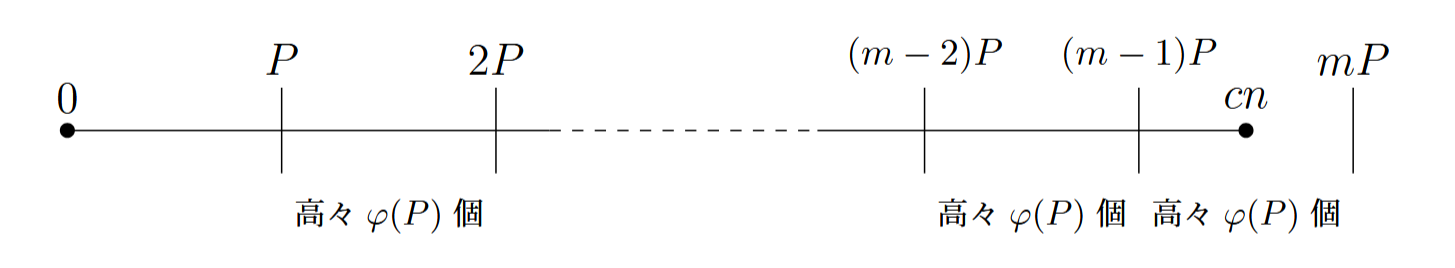 イメージ
イメージ
$1$から$P$までの素数は$P$の素因数の可能性があります. となるとその数は$P$の素因数の個数$+\varphi(P)$で抑えられますね. 都合の良い$P$は素因数が分かりやすく, できる限り$P$に対して$\varphi(P)$が小さいものですから, $P=p_k\#$などがよいでしょう.
(最初変なことをしますが, 適する$k$を探してるだけです.)
$p_k$以下の正の整数は$p_k$以下の素因数しかもたないため
$$
\sum_{i=1}^{p_k}\frac{1}{i}<\prod_{i=1}^{k} \left(1+\frac{1}{p_i}+\frac{1}{p_i^2}+\cdots\right)=\prod_{i=1}^k \left(\frac{p_i}{p_i-1}\right)
$$
で最左辺は$p_k\to\infty$で発散するから, $\prod_{i=1}^k(p_i/(p_i-1))>2c$となるような$k$が存在する.
$N=2k+\dfrac{p_k\#}{c}$とし, また$\lfloor cn\rfloor=m(p_k\#)-x\quad (0\leq x< p_k\#)$と非負整数$m, x$を用いて表す. このとき, $1$から$p_k\#$までに素数は高々$k+\varphi(p_k\#)$個であり, $i$を$2$以上$m-1$以下の整数とするとき, $i(p_k\#)$から$(i+1)(p_k\#)$までに素数は高々$\varphi(p_k\#)$個あるから
$$
\pi (cn)\leq m\varphi(p_k\#)+k
$$
である. さて
$$
\varphi(p_k\#) = p_k\# \prod_{i=1}^k \left( \frac{p_i - 1}{p_i} \right) = \frac{p_k\#}{\prod_{i=1}^k \left( \frac{p_i}{p_i - 1} \right)} < \frac{p_k\#}{2c}
$$
であるから
$$
\pi (cn)<\frac{mp_k\#}{2c}+k=\frac{\lfloor cn\rfloor}{2c}+\frac{2ck+x}{2c}<\frac{n}{2}+\frac{2ck+p_k\#}{2c}< n
$$
となる. これは, $p_n>cn$であることを意味する.
(やや式がいかついのですが, 大小評価をやってるだけで, 難しいところは特にありません)
準備もできたので次の定理を証明します:
任意の正数$c$に対し, ある$N$が存在し$n>N$なる任意の正の整数$n$に対して, $p_n\#>p_{n+1}^c$が成り立つ.
任意の実数に対し, それよりも大きい整数が存在するため, $c$が整数のときに証明すれば十分である.
Bonseの不等式の証明と同じように, $4$以上の整数$k$に対し, $p_k\#>p_{k+p_k-1}$が成り立つ. また十分大きい整数$k$に対し, $p_k>ck$が成り立つので, $p_k\#>p_{(c+1)k}$である.
したがって
$$
\begin{align*}
p_{ck}\#>&(p_k\#)^c>p_{(c+1)k}^c>p_{ck+1}^c\\
p_{ck+1}\#>&(p_k\#)^c>p_{(c+1)k}^c>p_{ck+2}^c\\
&\vdots\\
p_{(c+1)k-1}\#>&(p_k\#)^c>p_{(c+1)k}^c
\end{align*}
$$
であるから, 十分大きい$n$に対して, $p_n\#>p_{n+1}^c$が成り立つことが示された.
これ以上の一般化となると難しそうですね.
