Farkasの補題と線形計画問題の双対定理

まず$1\land2$は成り立たないことを示す．
$(\lnot1\Rightarrow2)$
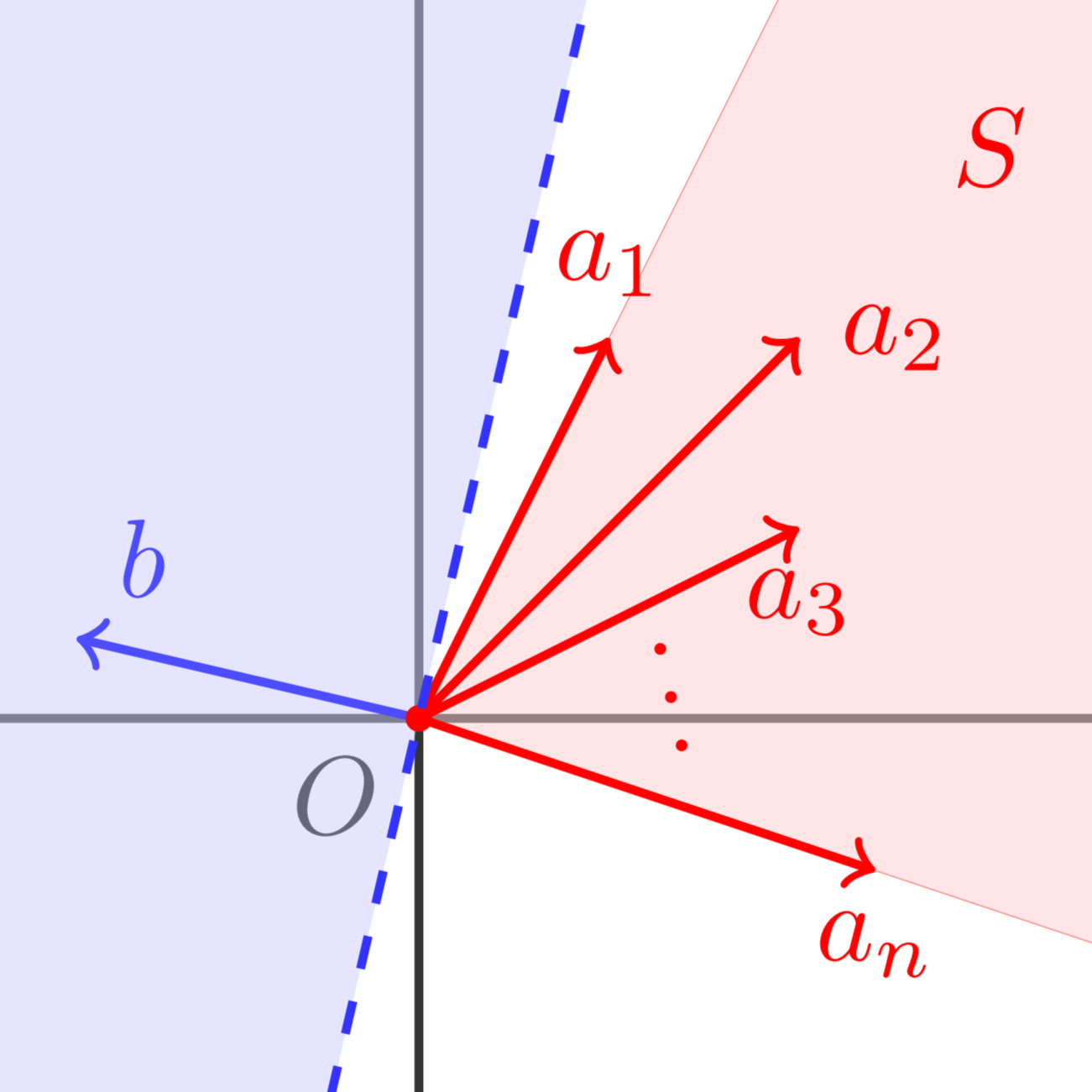
$1$が成り立たないとする．$S:=\{y\in\R^m\vert\exists x\in\R^n,y=Ax,x\geq0\}$は閉凸集合であることは容易に確かめられる．よって，$b\notin S$であるから 分離超平面定理 より，$\forall y\in S,\ip{a}{b}>\alpha\geq\ip{a}{y}$となるような$a\in\R^m\setminus\{0\}$と$\alpha\in\R$が存在する．
証明のイメージ図：ベクトル$a_i\,(i=1,\cdots,n)$はそれぞれ，基底$e_i\,(i=1,\cdots,n)$を行列$A$で写したもの．
ここで$0\in S$と$y\in S$の任意性により$\ip{a}{b}>\alpha\geq0$なので，$\ip{a}{b}>0$がわかる．

$(1\Rightarrow\lnot2)$
$1\land2$が偽であることを確かめるため，真であると仮定して，背理法を用いる．実際，$0=\ip{x}{A^ty}=\ip{Ax}{y}\leq\ip{b}{y}<0$となって矛盾が生じるので命題は確かめられた．
$(2\Rightarrow \lnot1 )$
$2$すなわち，$\exists y\in\R^m,\,A^ty=0,\ip{b}{y}<0,I_my=y\geq0$を仮定する．ただし，$I_m$は$m$次単位行列．
そこで上の仮定から，
\begin{align} &\exists y\in\R^m,\A y\geq0,\ip{b}{y}<0\cdots(*)\text{が従うので，}\\ (*)\eqv&\nexists(x,\lambda)\in\R^n\times\R^m, \A^t\xl=\At\xl=b,\xl\geq0\leftarrow(\because \text{Farkasの補題})\\ \eqv&\nexists(x,\lambda)\in\R^n\times\R^m,Ax+\lambda=b, x\geq0,\lambda\geq0\\ \eqv&\nexists x\in\R^n,Ax\leq b, x\geq0 \end{align}となり，$2$から$\lnot1$が導かれた．$\square$

\begin{align} x^M&:(P)\text{の実行可能解}\\ y^m&:(D)\text{の実行可能解}\\ &\text{と仮定する．このとき，}\\ \max(P)&=\ip{c}{x^M}\\ &\leq\ip{A^ty^m}{x^M}\leftarrow(\because x^M\geq0,A^ty^m\geq c)\\ &=\ip{Ax^M}{y^m}\\ &\leq\ip{b}{y^m}\leftarrow(\because y^m\geq0,Ax^M\leq b)\\ &=\min(D). \end{align} $\square$

主問題(P)もその双対問題(D)もともに実行可能解をもつと仮定する．このとき弱双対定理から$\max(P)\leq\min(D)$は既知なので，$\max(P)<\min(D)$とならないことを示す．
背理法を用いて$\max(P)<\min(D)=:\gamma$を仮定する．このとき，$\max(P)<\gamma$より，
\begin{align} &\nexists\xb\in\R^n,c^t\xb=\ip{c}{\xb}\geq\gamma,A\xb\leq b,\xb\geq 0\\ \eqv&\nexists\xb\in\R^n,(-c)^t\xb\leq-\gamma,A\xb\leq b,\xb\geq 0\\ \follow&\exists(\yb,\lambda)\in\R^m\times\R,\Ac^t\yl=\Act\yl=0,\\ &\bg^t\yl\geq0,\yl\geq0\\ &(\because\text{Farkasの補題 系})\\ \eqv&\exists\yb\in\R^m,\exists\lambda\in\R,A^t\yb=\lambda c,\ip{b}{\yb}<\lambda\gamma,\yb\geq0,\lambda\geq0\cdots(**) \end{align}が従う．

1. $\lambda=0$のとき
   \begin{align} (**)\eqv&\exists\yb\in\R^m,A^t\yb=0,\ip{b}{\yb}<0,\yb\geq0\\ \eqv&\nexists x'\in\R^n,Ax'\leq b,x'\geq0\,(\because\text{Farkasの補題 系}) \end{align}
   となって，主問題(P)が実行可能であるということに反する．
2. $\lambda>0$のとき
   \begin{align} (**)\follow\exists\yb/\lambda\in\R^m,A^t(\yb/\lambda)=c,\ip{b}{\yb/\lambda}&<\gamma\\ &=\max(P)\\ &\leq\min(D)\,(\because\text{弱双対定理}) \end{align}
   が導出され，$\yb/\lambda$が双対問題(D)の実行可能領域にあるので，$\ip{b}{\yb/\lambda}<\min(D)$は矛盾．

したがって(1),(2)両方とも矛盾が生じたので，$\max(P)<\min(D)$は成り立たず，弱双対定理から$\max (P)=\min(D)$が成立．$\square$