【光学】円孔による回折
回折とは
回折(diffraction)とは,空間中に伝わる波が衝立のような障害物の裏側に回り込んで伝わる現象をいう.この現象は,1665年にイタリアの数学者・物理学者であったフランチェスコ・マリア・グリマルディ[1]により初めて報告された.初等的にはホイヘンスの原理を用いて説明される.
光の回折
スリットに入射した光のスリットに近いところで観測される回折をフレネル回折(Fresnel diffraction)[2]といい,無限遠で観測される回折をフラウンホーファー回折(Fraunhofer diffraction)[3]という.
今回はそのフレネル回折とフラウンホーファー回折の中間的な回折現象である円孔による回折について扱う.
円孔による回折
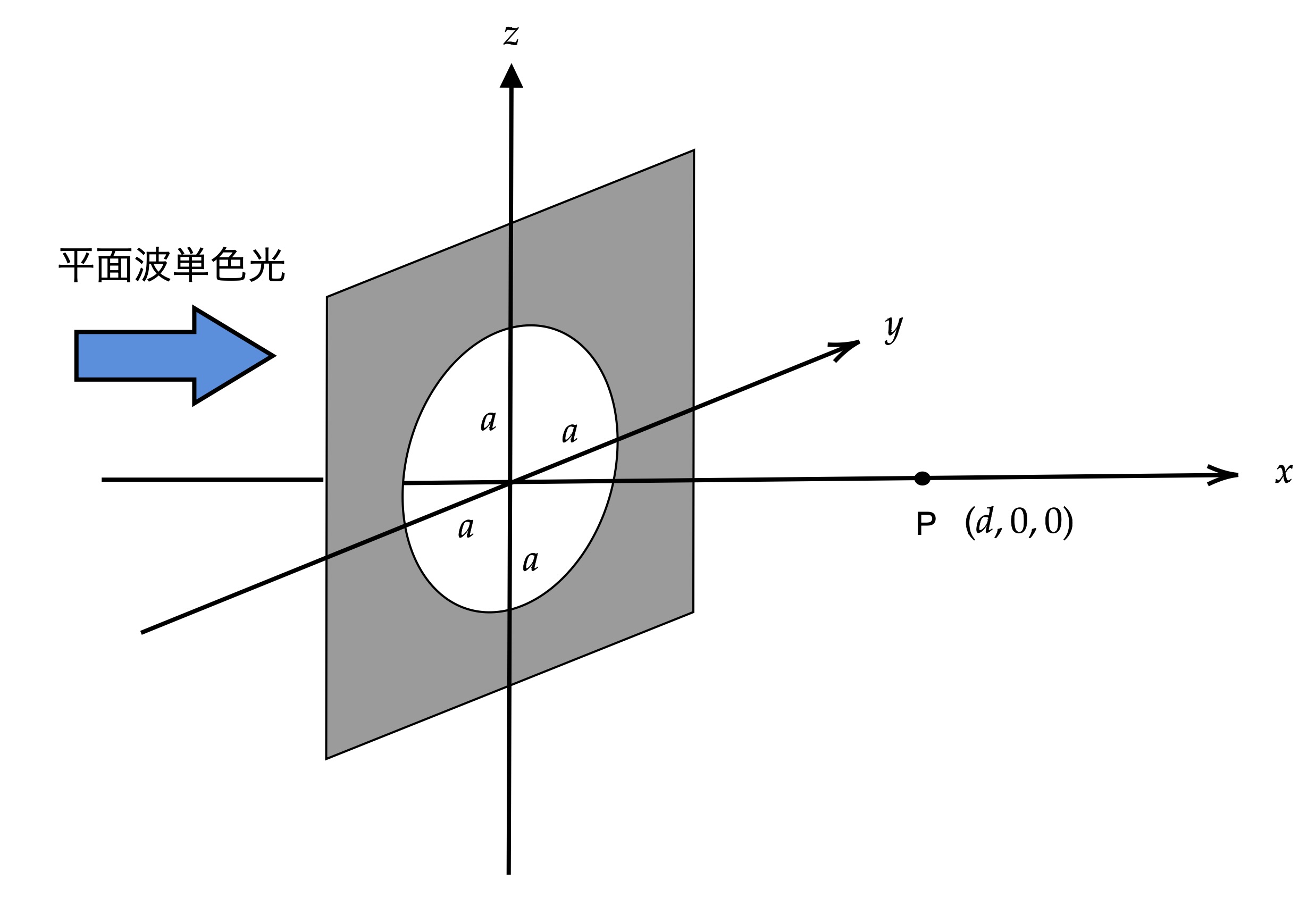 円孔
円孔
図1のように,$y-z$平面に半径$a$の円孔の開けられた板が置かれ,円孔の中心$\mathrm{O}$を原点に,円孔に垂直に$x$軸をとり,$x$軸上で光の強度を観測する.$x$軸上の負方向から波長$\lambda$の一様な強さの平面波の光を円孔にあてる.$x$軸上に適当な点$\mathrm{P}(d,0,0)$をとり,
$$ \mathrm{A}_{k}\mathrm{P}-\mathrm{OP}=k\frac{\lambda}{2}~~~(k=1,2,3,\cdots,n-1)~~~(n\in\mathbb{N}) $$
となるように,円孔内で$y$軸上正方向に点$\mathrm{A}_{1},\mathrm{A}_{2},\cdots,\mathrm{A}_{n-1}$を円周常に点$\mathrm{A}_{n}$をとる.ただし,$a,\lambda\ll d$とし,円孔内の各点を通過した光は$x>0$の領域へ,どの方向にも同じ強さで進行し,減衰は無視できるものとする.
$\mathrm{OA}_{1}=r_{1},\mathrm{OA}_{2}=r_{2},\cdots,\mathrm{OA}_{n}=r_{n}=a$とおくとき,半径$r_{k}$と$r_{k+1}$$(k=1,2,3,\cdots,n-1)$の同心円で囲まれた輪帯$C_{k}$の面積を求めよ.また,$C_{k}$の面積が近似的に$k$の値によらず一定とみなすことができることを示せ.
このとき,ほぼ面積の等しい隣り合う輪帯を通過したほぼ同じ強さの光は光路が互いに$\frac{\lambda}{2}$ずつずれているので,隣り合う輪帯の光は,$x$軸上の点$\mathrm{P}$で重ね合わされると干渉により互いに打ち消し合う.このように分けられた同心の輪帯をフレネルの半波長帯という.フレネルは,この輪帯を用いて光の回折現象を考察した.光の強度が極小となり暗くなる点$\mathrm{P}$までの点$\mathrm{O}$からの距離$d$を求めよ.
(1)
輪帯$C_{k}$の面積を求める.三角形$\mathrm{OA}_{k}\mathrm{P}$について,三平方の定理より,
$${r_{k}}^{2}+d^{2}=(\mathrm{A}_{k}\mathrm{P})^{2}$$
が成り立ち,$\mathrm{A}_{k}\mathrm{P}$の定義$\mathrm{A}_{k}\mathrm{P}-d=k\frac{\lambda}{2}$より,
$${r_{k}}^{2}=\left(k\frac{\lambda}{2}+d\right)^{2}-d^{2}=k^{2}\frac{\lambda^{2}}{4}+k\lambda d$$
となる.ここで,求める輪帯$C_{k}$の面積は$C_{k}=\pi\left({r_{k+1}}^{2}-{r_{k}}^{2}\right)$と表されるので,
\begin{align}
C_{k}&=\pi\left({r_{k+1}}^{2}-{r_{k}}^{2}\right)\notag\\
&=\pi\left(\left(\left(k+1\right)^{2}\frac{\lambda^{2}}{4}+\left(k+1\right)\lambda d\right)^{2}-\left(k^{2}\frac{\lambda^{2}}{4}+k\lambda d\right)^{2}\right)\notag\\
&=\pi\left(k\frac{\lambda^{2}}{2}+\frac{\lambda^{2}}{4}+\lambda d\right)=\pi d\lambda\left(1+\frac{2k+1}{4}\frac{\lambda}{d}\right)\fallingdotseq\pi d\lambda\notag
\end{align}
これより,円環の面積は$k$の値によらず近似的に一定である.
(2)
(1)の補足にあるように,各円環から点$\mathrm{P}$までの距離が$\frac{\lambda}{2}$ずつずれているから,円孔に一様な強さの光が照射されると,隣り合う円環からの光は互いに打ち消し合う.よって,nが偶数$(n=2m,m=1,2,3,\cdots)$のとき,強度は極小になる.つまり,暗くなる条件は,
$$A_{n}P-d=2m\frac{\lambda}{2}$$
と表され,
$$A_{n}P-d=\sqrt{d^{2}+a^{2}}-d=d\sqrt{1+\left(\frac{a}{d}\right)^{2}}-d\fallingdotseq\frac{a^{2}}{2d}$$
より,$x$軸上で光の強度が極小になる位置は,
$$d=\frac{a^{2}}{2n\lambda}$$
である.