文献あり

重複円順列について

310

はじめに

重複円順列について、分かりやすく説明してくれている動画dougaを見つけて面白かったので
自分なりに考えてまとめてみました。
頭の中で整理しきれていない部分もあるので、そのうち書き直すかも
強調されている言葉は基本的に造語なので注意してください。

問題

赤玉6個と白玉6個を円形に並べる方法は何通りあるか

イメージ

少し俗っぽい設定に変更して考えるとイメージし易い。イメージを描きにくいときは問題を次のように読みかえるのも良い。

「12席ある回転テーブルに2種類、各6個ずつある料理をセッティングする。セッティングの仕方は何通りあるか」

この問題を考えるときは「テーブル上の料理の配置」と「各人への料理の割り当て」の2つの視点を比べながらみていくのが良いと思われる。
後者は本質的に、重複したものを1列に並べる作業とみなせる。
以降は、前者を配置、後者を配列とよび分けることにする。
また、テーブルの回転については$\displaystyle\frac{1}{12}$回転させる操作が最小単位になるので、この操作を基本操作とよぶことにする。

もう一つのイメージとして、配列を無限につなぎ合わせたものを考える。それが同じものと言えるような配列は配置として一致する。後述の周期を考えるときはこちらのイメージの方がしっくりくるかも。

方針

配列が何通りあるかは、いわゆる重複順列なので容易に計算できる。
一般に１つの配置が複数の配列に対応する。
配列Aと配列Bが配置として重複する→配列Aに基本操作を何回か行うと配列Bになる
そこで、重複順列の数から、配置として重複する配列の数を除いていく方法を考えていく。

周期

ある配列に基本操作を$k$回行うと元の配列に重なるとき、その「配列は周期$k$をもつ」ということにする。

自明な周期

基本操作を１周分（今回は12回）行うと、どんな配列でも元の配列と重なる。
よって、すべての配列は周期12をもつ。これを自明な周期とよぶことにする。

非自明な周期

配列によっては、自明な周期よりも短い周期をもつ。例えば次の配列
WBWBWBWBWBWB
は周期として12,6,4,2を持つ。
8回、10回の基本操作でも配列は重なるが、周期としては採用しない。
逆回転を考えるとそれぞれ周期4、周期2となるので本質的に余計（？）
周期のうち。最も短いものをその配列の固有周期、または単に、その配列の周期とよぶことにする。
配列の周期が$k$であるということは、同じ配置に$k$個の配列が対応していることを意味する。
ちなみに前述の配列の周期は2である。

ブロック

自明な周期よりも短い周期をもつ配列を考えると、同じ部分配列が繰り返されていることに気づく。
繰り返しの単位をブロックとよぶことにする。
配列を大きさ$s$のブロックに分けることができるとき、$s$回の基本操作でブロック1つ分動くことになる。よって、そのとき配列は周期$\displaystyle\frac{12}{s}$をもつ

表

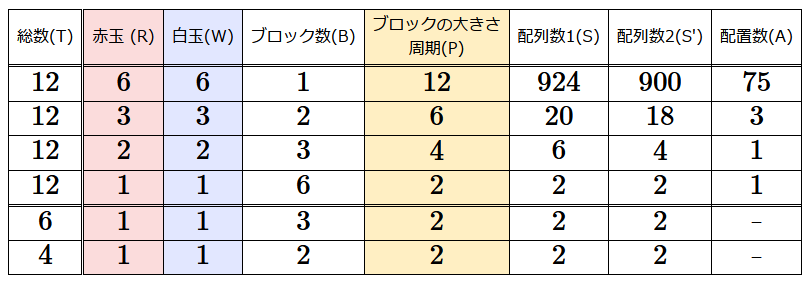ブロックと配列数の表
少し唐突だが、今までの議論をもとに上のような表を導入する。
以下に各項目について簡単に説明する。

総数(T)：議論している（部分）配列の長さ
赤玉(R)：配列に含まれる赤玉の個数
白玉(W)：配列に含まれる白玉の個数
ブロック数(B)：配列を何個のブロックに分けるか
ブロックの大きさ(P)：周期でもある。値としては$\displaystyle\frac{T}{B}$
配列数1(S)：ブロックを構成する部分は配列は何通りあるか（より小さく分割可能な配列を含む）
値は${}_P\mathrm{C}_{R}$
配列数1(S')：ブロックを構成する部分配列は何通りあるか（それ以上分割できないもの）
R、W、Pの公約数が１のみであればSと一致する
配置数(A)：配置の数。値としては$\displaystyle\frac{S'}{P}$

表を埋める手順

1行目のT、R、W、B、Pはそのまま記載。
R、W、Pが1より大きな公約数をもつとき、その約数を$d$とすると、大きさ$\displaystyle\frac{P}{d}$、個数$d$のブロックに分割可能な部分配列が存在する。
12,6,6の共通の約数は2,3,6なのでそれぞれの行を用意してBの欄に約数を記載
そのようにして生まれた行を元の行の「子」とよぶことにする。
W、Rの欄には、「親」の行の数字をブロック数で割ったものを記載
Tの欄には「親」の行のPを記載
Pの欄には$\displaystyle\frac{T}{B}$を記載
Sの欄にはR,Wを並べる重複順列の数を記載
T、R、Wの公約数が１のみであればS'にもSの値を記載する
「子」の情報がそろったらS'が空欄の箇所に次の値を記載する
　　　S'＝S－（子のS'を合計したもの）
S'が埋まったらAの欄に$\displaystyle\frac{S'}{P}$を記載（Tが12のものだけで可）　　　
同様の手順を表が埋まるまでまで繰り返す